分类目录:《深入理解深度学习》总目录
在实践中,当给定相同的查询、键和值的集合时,我们希望模型可以基于相同的注意力机制学习到不同的行为, 然后将不同的行为作为知识组合起来, 捕获序列内各种范围的依赖关系 (例如,短距离依赖和长距离依赖关系)。 因此,允许注意力机制组合使用查询、键和值的不同子空间表示(Representation Subspaces)可能是有益的。
为此,与其只使用单独一个注意力汇聚, 我们可以用独立学习得到的组不同的 线性投影(Linear Projections)来变换查询、键和值。 然后,这组变换后的查询、键和值将并行地送到注意力汇聚中。 最后,将这个注意力汇聚的输出拼接在一起, 并且通过另一个可以学习的线性投影进行变换, 以产生最终输出。 这种设计被称为多头注意力(Multihead Attention)。 对于个注意力汇聚输出,每一个注意力汇聚都被称作一个头(Head)。 下图展示了使用全连接层来实现可学习的线性变换的多头注意力:
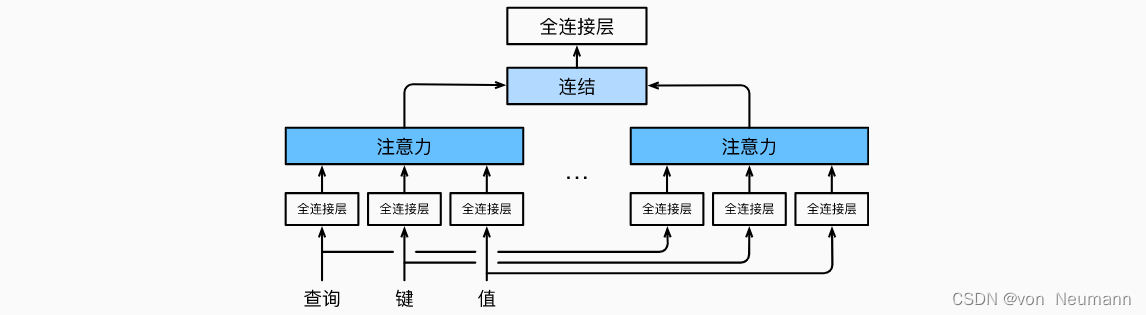
给定查询 q ∈ R d q q\in R^{d_q} q∈Rdq、 键 k ∈ R d k k\in R^{d_k} k∈Rdk和值 v ∈ R d v v\in R^{d_v} v∈Rdv, 每个注意力头 h i ( i = 1 , 2 , ⋯ , h ) h_i(i=1, 2, \cdots, h) hi(i=1,2,⋯,h)的计算方法为:
h i = f ( W i ( q ) q , W i ( k ) k , W i ( v ) v ) ∈ R p v h_i=f(W_i^{(q)}q, W_i^{(k)}k, W_i^{(v)}v)\in R^{p_v} hi=f(Wi(q)q,Wi(k)k,Wi(v)v)∈Rpv
其中,可学习的参数包括 W i ( q ) ∈ R p q × d q W_i^{(q)}\in R^{p_q\times d_q} Wi(q)∈Rpq×dq、 W i ( k ) ∈ R p k × d k W_i^{(k)}\in R^{p_k\times d_k} Wi(k)∈Rpk×dk和 W i ( v ) ∈ R p v × d v W_i^{(v)}\in R^{p_v\times d_v} Wi(v)∈Rpv×dv以及代表注意力汇聚的函数 f f f。 f f f可以是《深入理解深度学习——注意力机制(Attention Mechanism):注意力评分函数(Attention Scoring Function)》中的加性注意力和缩放点积注意力。 多头注意力的输出需要经过另一个线性转换, 它对应着 h h h个头连结后的结果,因此其可学习参数是 W i ( o ) ∈ R p p × h p v W_i^{(o)}\in R^{p_p\times h_{p_v}} Wi(o)∈Rpp×hpv:
W o [ h 1 h 2 ⋮ h h ] ∈ R p o W_o \begin{gather*} \begin{bmatrix} h_1 \\ h_2 \\ \vdots \\ h_h \end{bmatrix} \end{gather*} \in R^{p_o} Wo h1h2⋮hh ∈Rpo
基于这种设计,每个头都可能会关注输入的不同部分, 可以表示比简单加权平均值更复杂的函数。
参考文献:
[1] Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015
[2] Aston Zhang, Zack C. Lipton, Mu Li, Alex J. Smola. Dive Into Deep Learning[J]. arXiv preprint arXiv:2106.11342, 2021.


