 翻译:
翻译:
给您一个带有𝑛顶点的加权树。回想一下,树是一个没有任何循环的连通图。加权树是每条边都有一定权重的树。树是无向的,它没有根。
因为树木让你厌烦,所以你决定挑战自己,在给定的树上玩一款游戏。
在移动中,您可以从一个节点移动到它的一个邻居(与它有直接边的另一个节点)。
你从一个变量𝑥开始,它最初等于0。当您通过边缘𝑖时,𝑥将其值更改为𝑥𝖷𝖮𝖱𝑤𝑖(其中𝑤𝑖是𝑖-th边缘的权重)。
您的任务是从顶点𝑎到顶点𝑏,但是当且仅当到达节点𝑏后,𝑥的值将变为0时,允许您进入节点𝑏。换句话说,您只能通过使用边缘𝑖来访问节点𝑏,这样𝑥𝖷𝖮𝖱𝑤𝑖=0。一旦你进入节点𝑏,游戏就结束了,你就赢了。
此外,你最多可以在任何时间点传送一次到除顶点𝑏外的任何顶点。你可以从任何顶点传送,甚至从𝑎。
如果你能从𝑎到达顶点𝑏,回答“YES”,否则回答“NO”。
注意,𝖷𝖮𝖱表示按位异或操作。
输入
第一行包含一个整数𝑡(1≤𝑡≤1000)——测试用例的数量。
每个测试用例的第一行分别包含三个整数𝑛、𝑎和𝑏(2≤𝑛≤105),(1≤𝑎,𝑏≤𝑛;𝑎≠𝑏)——顶点的数量,以及起始节点和期望的结束节点。
接下来的每一行𝑛−1表示树的一条边。边缘𝑖用三个整数𝑢𝑖,𝑣𝑖和𝑤𝑖——顶点连接的标签(1≤𝑢𝑖,𝑣𝑖≤𝑛;𝑢𝑖≠𝑣𝑖;1≤𝑤𝑖≤109)的重量和各自的优势。
可以保证所有测试用例中𝑛的总和不超过105。
输出
对于每个测试用例,如果你能到达顶点𝑏,输出“YES”,否则输出“NO”。
例子
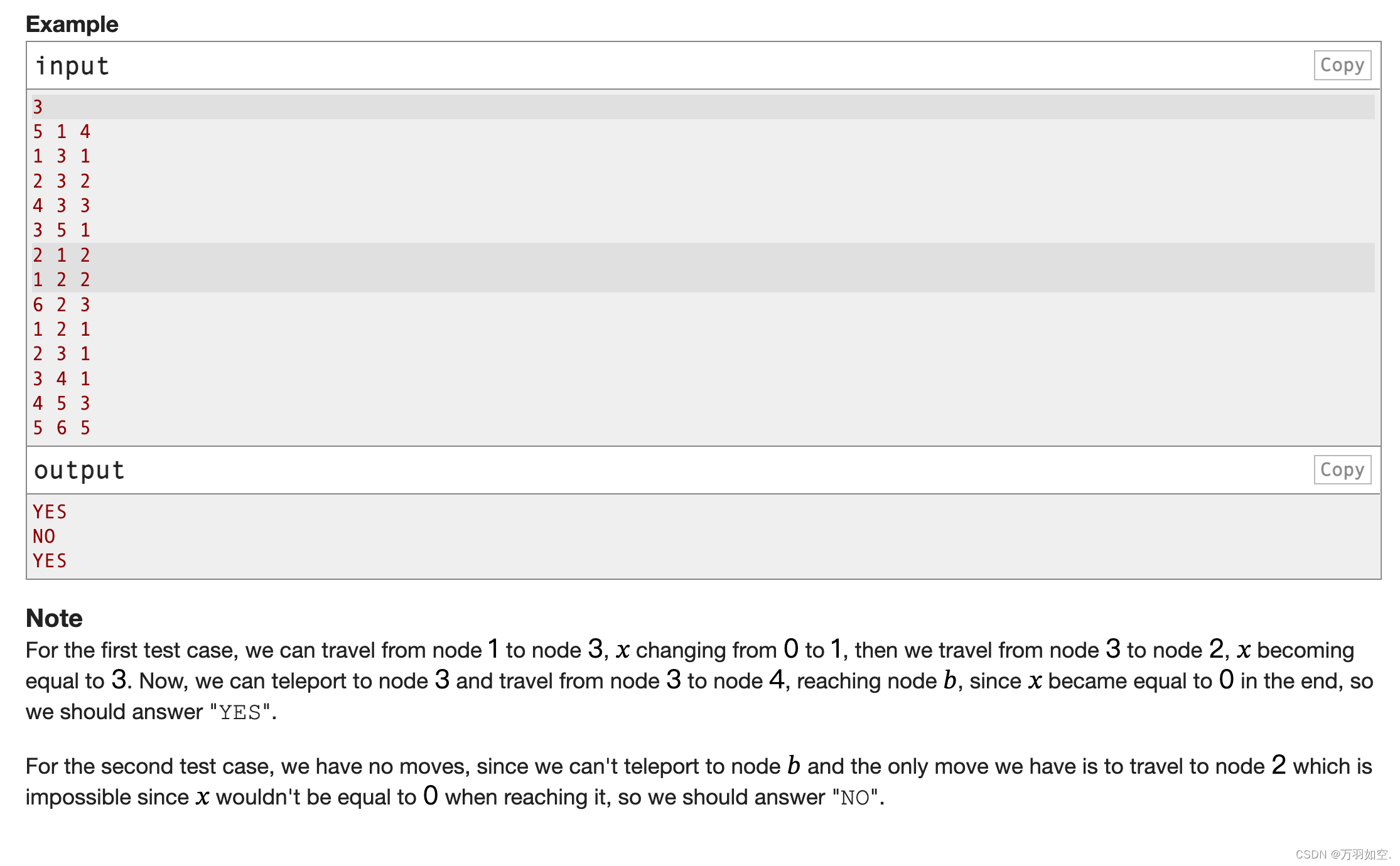
inputCopy
3.
5 1 4
1 3 1
2 3 2
4 3 3
3 5 1
2 1 2
1 2 2
6 2 3
1 2 1
2 3 1
3 4 1
4 5 3
5 6 5
outputCopy
是的
没有
是的
请注意
对于第一个测试用例,我们可以从节点1移动到节点3,𝑥从0变为1,然后我们从节点3移动到节点2,𝑥变为等于3。现在,我们可以传送到节点3,并从节点3移动到节点4,到达节点𝑏,因为𝑥最终变成了0,所以我们应该回答“YES”。
对于第二个测试用例,我们没有移动,因为我们不能传送到节点𝑏,我们唯一的移动是移动到节点2,这是不可能的,因为𝑥到达节点2时不等于0,所以我们应该回答“no”。
思路:
无向图,a到达b路径上一直异或,到最后到达为0,中间可以传送到任何一个地点。那么我们只需要跑两个dfs,然后看知道到相互的点是否直接为0,或者有点有相同的值即可。
代码:
#include <iostream>
#include <algorithm>
#include <string.h>
#include <string>
#include <math.h>
#include <stdio.h>
#include<vector>
#include<queue>
#include<map>
#include<set>
#include<tuple>
#include<numeric>
#include<stack>
using namespace::std;
typedef long long ll;
int n,t;
inline __int128 read(){__int128 x = 0, f = 1;char ch = getchar();while(ch < '0' || ch > '9'){if(ch == '-')f = -1;ch = getchar();}while(ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}return x * f;
}
inline void print(__int128 x){if(x < 0){putchar('-');x = -x;}if(x > 9)print(x / 10);putchar(x % 10 + '0');
}int a,b;
int x,y,z;
map<ll,int>we;
ll dd[100005];
int jjk=0;
set<ll>wee;
vector<pair<int,int>>q[100005];
void dfs(int x,int fa){if (x==b) {if (dd[x]==0) {jjk=1;}return;}for (int i =0; i<q[x].size(); i++) {if (q[x][i].first==fa) {continue;}dd[q[x][i].first]=dd[x]^q[x][i].second;if (q[x][i].first!=b) {we[dd[q[x][i].first]]=1;}dfs(q[x][i].first, x);}
}
void dfs2(int x,int fa){if (we[dd[x]]&&x!=b) {
// printf("%d \n",x);
// printf("dsa\n");jjk=1;}
// if (dd[x]==0) {
// jjk=1;
// }for (int i =0; i<q[x].size(); i++) {if (q[x][i].first==fa) {continue;}dd[q[x][i].first]=dd[x]^q[x][i].second;dfs2(q[x][i].first, x);}
}
void solv(){we.clear();jjk=0;cin>>n>>a>>b;for (int i =0; i<=n; i++) {q[i].clear();}for (int i =1; i<n; i++) {cin>>x>>y>>z;q[x].push_back({y,z});q[y].push_back({x,z});}
// if (n==2) {
// printf("NO\n");return;
// }
// for (int i =1; i<=n; i++) {
// dd[i]=0;
// }
//dd[a]=0;dfs(a,a);
// for (int i =1; i<=n; i++) {
// printf("%lld ",dd[i]);
// }printf("\n");
// for (int i =1; i<=n; i++) {
// dd[i]=0;
// }dd[b]=0;we[0]=1;dfs2(b, b);
// for (int i =1; i<=n; i++) {
// printf("%lld ",dd[i]);
// }printf("\n");if (jjk) {printf("YES\n");return;}printf("NO\n");
// 4
// 4 3 2
// 3 1 1
// 1 4 1
// 1 2 3
}
int main(){ios::sync_with_stdio(false);cin.tie(); cout.tie();cin>>t;while (t--) {solv();}return 0;
}