梯度提升算法是最常用的集成机器学习技术之一，该模型使用弱决策树序列来构建强学习器。这也是XGBoost和LightGBM模型的理论基础，所以在这篇文章中，我们将从头开始构建一个梯度增强模型并将其可视化。

梯度提升算法介绍

梯度提升算法（Gradient Boosting）是一种集成学习算法，它通过构建多个弱分类器，然后将它们组合成一个强分类器来提高模型的预测准确率。

梯度提升算法的原理可以分为以下几个步骤：

1. 初始化模型：一般来说，我们可以使用一个简单的模型（比如说决策树）作为初始的分类器。
2. 计算损失函数的负梯度：计算出每个样本点在当前模型下的损失函数的负梯度。这相当于是让新的分类器去拟合当前模型下的误差。
3. 训练新的分类器：用这些负梯度作为目标变量，训练一个新的弱分类器。这个弱分类器可以是任意的分类器，比如说决策树、线性模型等。
4. 更新模型：将新的分类器加入到原来的模型中，可以用加权平均或者其他方法将它们组合起来。
5. 重复迭代：重复上述步骤，直到达到预设的迭代次数或者达到预设的准确率。

由于梯度提升算法是一种串行算法，所以它的训练速度可能会比较慢，我们以一个实际的例子来介绍：

假设我们有一个特征集Xi和值Yi，要计算y的最佳估计

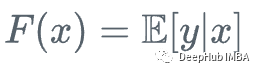
我们从y的平均值开始

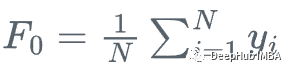
每一步我们都想让F_m(x)更接近y|x。

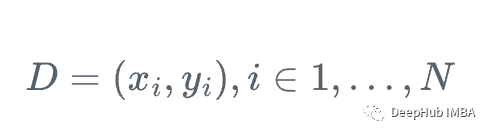
在每一步中，我们都想要F_m(x)一个更好的y给定x的近似。

首先，我们定义一个损失函数

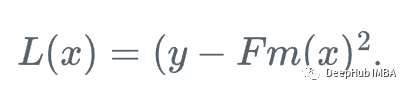
然后，我们向损失函数相对于学习者Fm下降最快的方向前进:

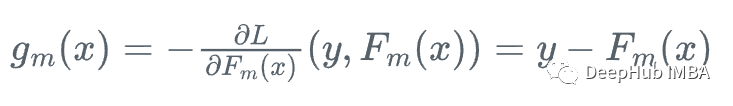
因为我们不能为每个x计算y，所以不知道这个梯度的确切值，但是对于训练数据中的每一个x_i，梯度完全等于步骤m的残差:r_i!

所以我们可以用弱回归树h_m来近似梯度函数g_m，对残差进行训练:

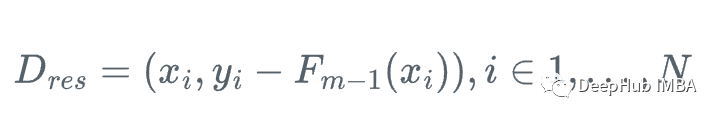
然后，我们更新学习器

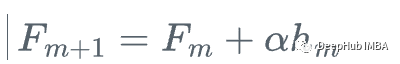
这就是梯度提升，我们不是使用损失函数相对于当前学习器的真实梯度g_m来更新当前学习器F_{m}，而是使用弱回归树h_m来更新它。

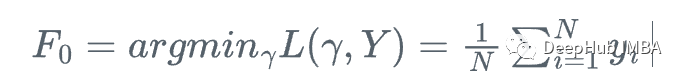
也就是重复下面的步骤

1、计算残差:

2、将回归树h_m拟合到训练样本及其残差(x_i, r_i)上

3、用步长\alpha更新模型

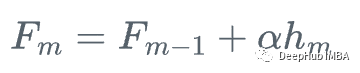
看着很复杂对吧，下面我们可视化一下这个过程就会变得非常清晰了

决策过程可视化

这里我们使用sklearn的moons 数据集，因为这是一个经典的非线性分类数据

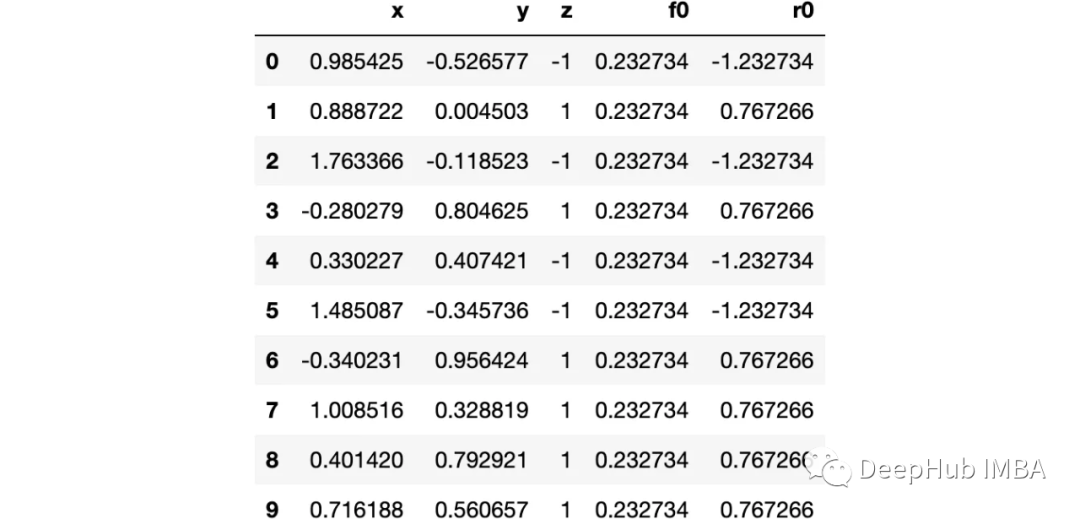
 import numpy as npimport sklearn.datasets as dsimport pandas as pdimport matplotlib.pyplot as pltimport matplotlib as mplfrom sklearn import treefrom itertools import product,isliceimport seaborn as snsmoonDS = ds.make_moons(200, noise = 0.15, random_state=16)moon = moonDS[0]color = -1*(moonDS[1]*2-1)df =pd.DataFrame(moon, columns = ['x','y'])df['z'] = colordf['f0'] =df.y.mean()df['r0'] = df['z'] - df['f0']df.head(10)

让我们可视化数据：

下图可以看到，该数据集是可以明显的区分出分类的边界的，但是因为他是非线性的，所以使用线性算法进行分类时会遇到很大的困难。

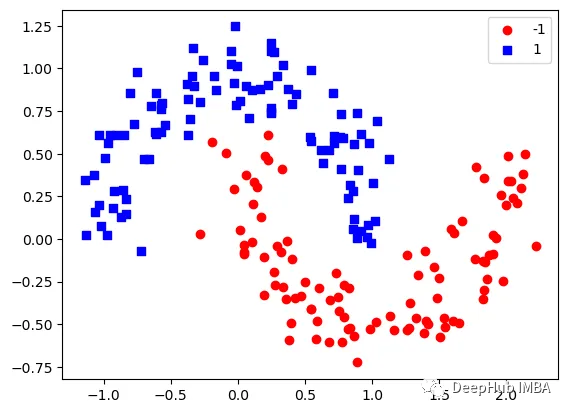
那么我们先编写一个简单的梯度增强模型:

 def makeiteration(i:int):"""Takes the dataframe ith f_i and r_i and approximated r_i from the features, then computes f_i+1 and r_i+1"""clf = tree.DecisionTreeRegressor(max_depth=1)clf.fit(X=df[['x','y']].values, y = df[f'r{i-1}'])df[f'r{i-1}hat'] = clf.predict(df[['x','y']].values)eta = 0.9df[f'f{i}'] = df[f'f{i-1}'] + eta*df[f'r{i-1}hat']df[f'r{i}'] = df['z'] - df[f'f{i}']rmse = (df[f'r{i}']**2).sum()clfs.append(clf)rmses.append(rmse)

上面代码执行3个简单步骤:

将决策树与残差进行拟合:

 clf.fit(X=df[['x','y']].values, y = df[f'r{i-1}'])df[f'r{i-1}hat'] = clf.predict(df[['x','y']].values)

然后，我们将这个近似的梯度与之前的学习器相加:

 df[f'f{i}'] = df[f'f{i-1}'] + eta*df[f'r{i-1}hat']

最后重新计算残差:

 df[f'r{i}'] = df['z'] - df[f'f{i}']

步骤就是这样简单，下面我们来一步一步执行这个过程。

第1次决策

Tree Split for 0 and level 1.563690960407257

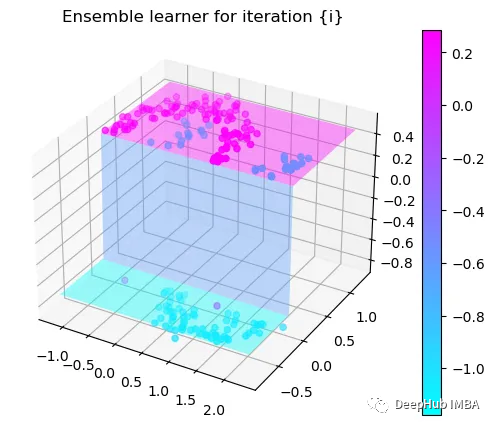
第2次决策

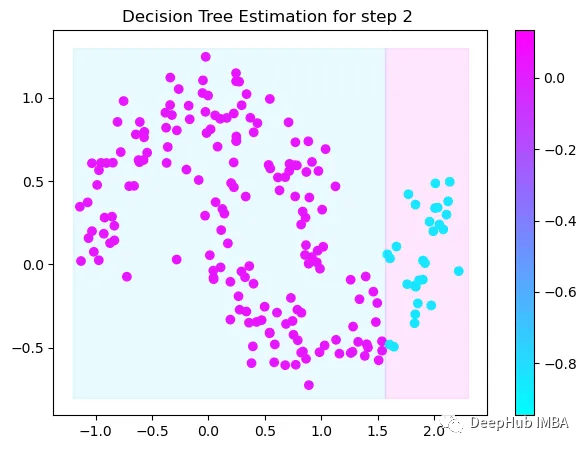
Tree Split for 1 and level 0.5143677890300751

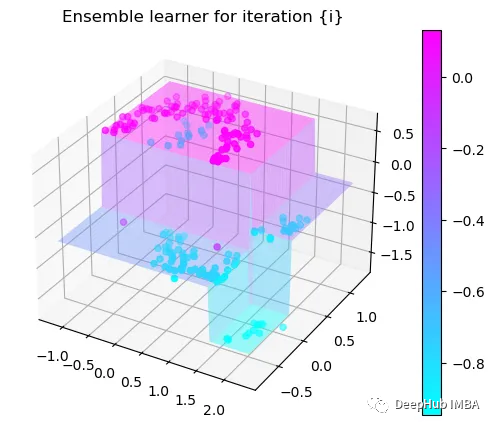
第3次决策

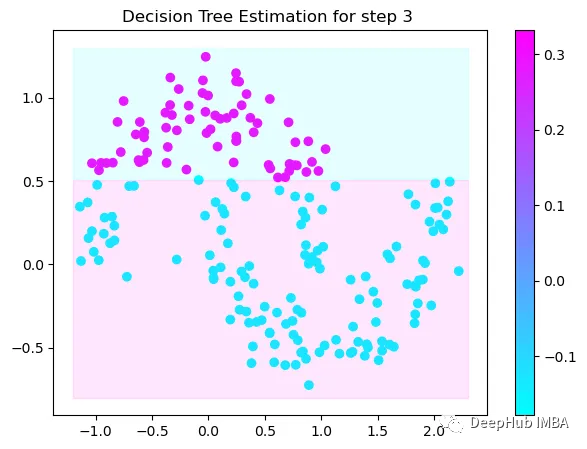
Tree Split for 0 and level -0.6523728966712952

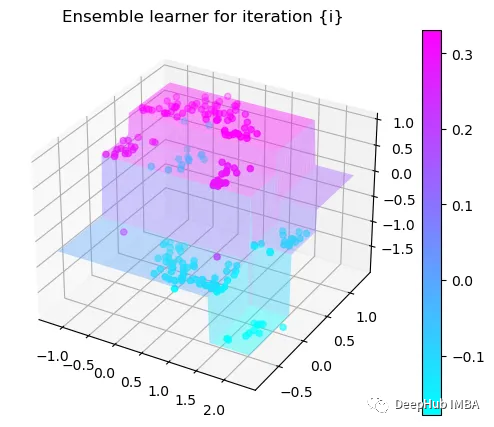
第4次决策

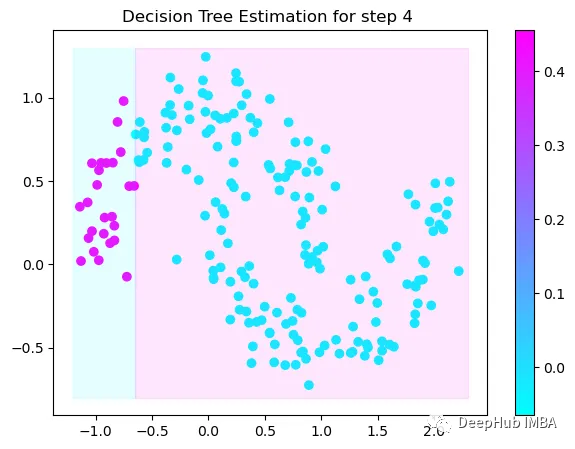
Tree Split for 0 and level 0.3370491564273834

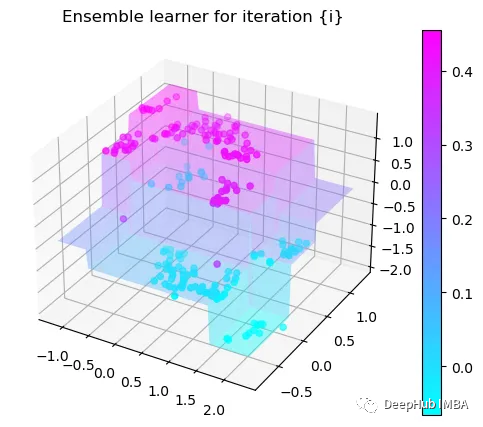
第5次决策

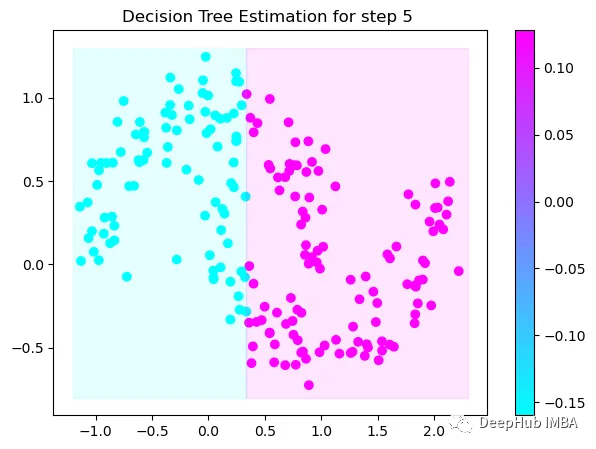
Tree Split for 0 and level 0.3370491564273834

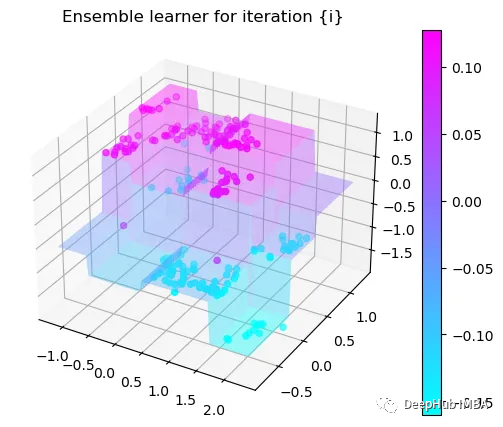
第6次决策

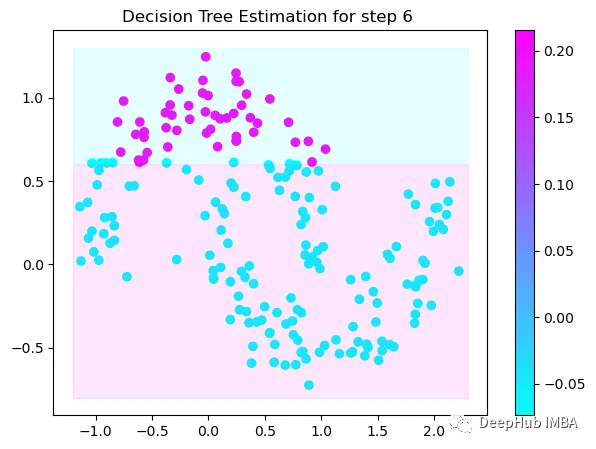
Tree Split for 1 and level 0.022058885544538498

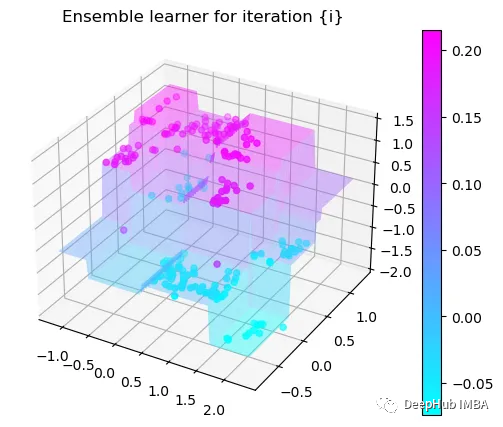
第7次决策

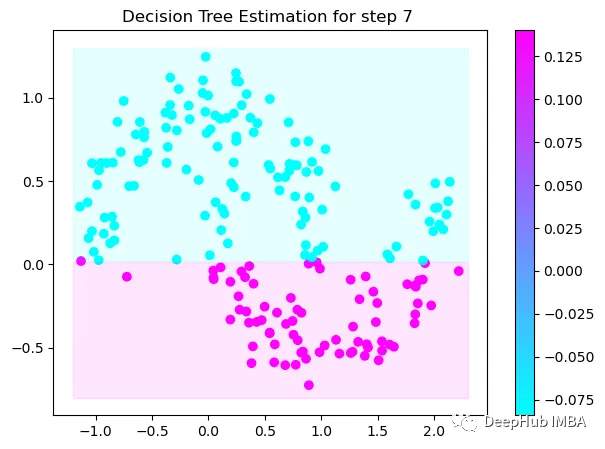
Tree Split for 0 and level -0.3030575215816498

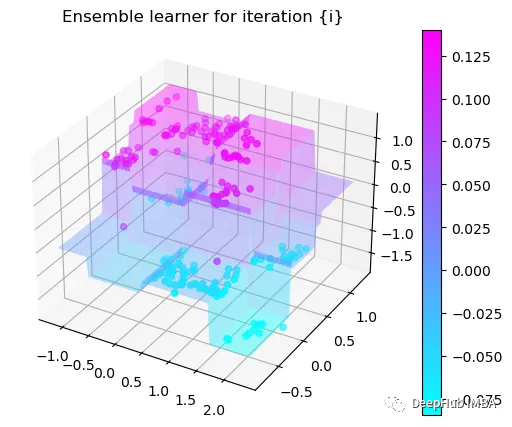
第8次决策

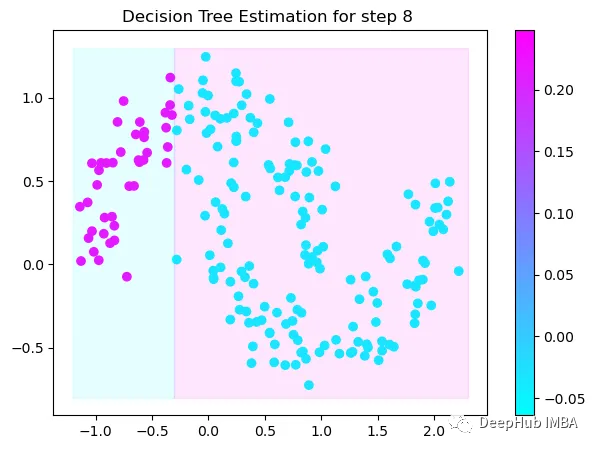
Tree Split for 0 and level 0.6119407713413239

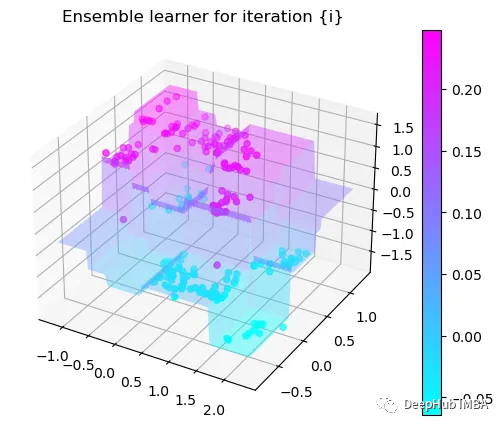
第9次决策

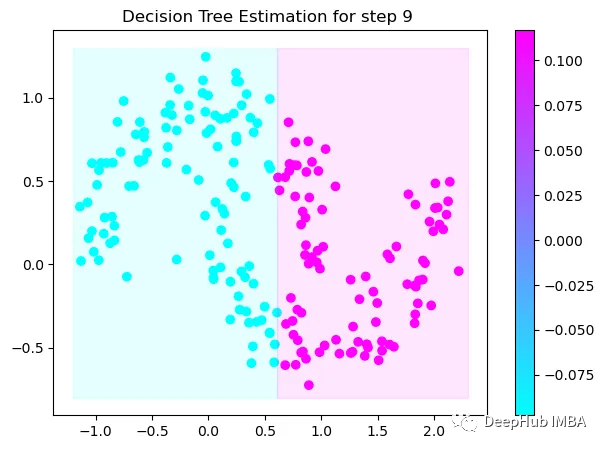
可以看到通过9次的计算，基本上已经把上面的分类进行了区分

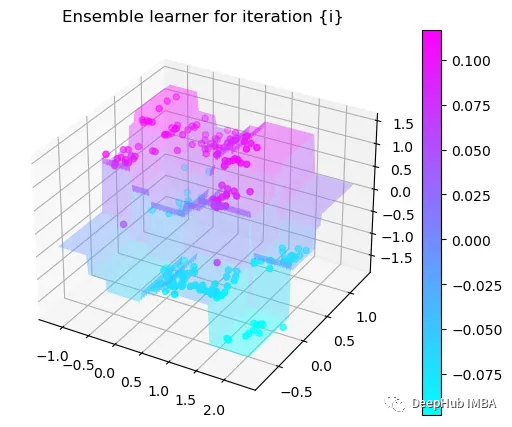
我们这里的学习器都是非常简单的决策树，只沿着一个特征分裂!但整体模型在每次决策后边的越来越复杂，并且整体误差逐渐减小。

 plt.plot(rmses)

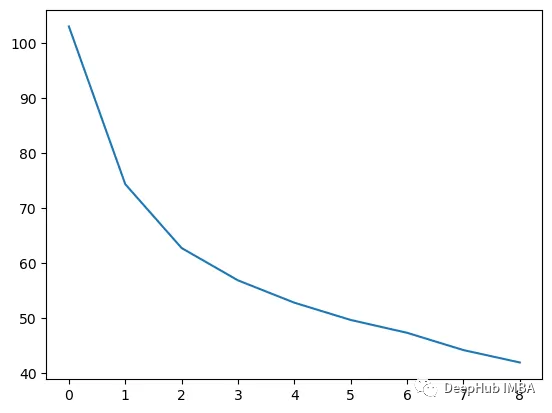
这也就是上图中我们看到的能够正确区分出了大部分的分类

如果你感兴趣可以使用下面代码自行实验：

https://avoid.overfit.cn/post/533a0736b7554ef6b8464a5d8ba964ab

作者:Tanguy Renaudie