文章目录
- 11 GMM——高斯混合模型
- 11.1 模型介绍
- 11.2 通过MLE估计参数
- 11.3 EM求解
11 GMM——高斯混合模型
11.1 模型介绍
从几何角度来说:
-
高斯混合模型表示:加权平均——由多个高斯分布混合叠加而成,如图
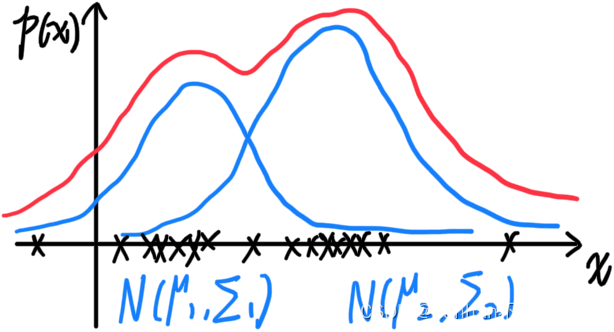
-
公式可以表达为:
p ( x ) = ∑ i = 1 K α i ⋅ N ( x ∣ μ i , Σ i ) , ∑ i = 1 K α i = 1 p(x) = \sum_{i=1}^K \alpha_i \cdot N(x|\mu_i, \Sigma_i), \quad \sum_{i=1}^K \alpha_i = 1 p(x)=i=1∑Kαi⋅N(x∣μi,Σi),i=1∑Kαi=1
若从混合模型的角度来说:
-
数据可以表示为:
{ x : X = { x i } i = 1 N z : Z = { z i } i = 1 N { z ∈ { C 1 , C 2 , … , C K } P ( z ) ∈ { p 1 , p 2 , … , p K } \begin{cases} x: X = {\lbrace x_i \rbrace}_{i=1}^{N} \\ z: Z = {\lbrace z_i \rbrace}_{i=1}^{N} \\ \end{cases} \qquad \begin{cases} z \in {\lbrace C_1, C_2, \dots, C_K \rbrace} \\ P(z) \in {\lbrace p_1, p_2, \dots, p_K \rbrace} \\ \end{cases} {x:X={xi}i=1Nz:Z={zi}i=1N{z∈{C1,C2,…,CK}P(z)∈{p1,p2,…,pK} -
其中 x x x表示ovserve variable, z z z表示latent variable
-
这里的隐变量 z z z表示样本X分别属于哪一个高斯
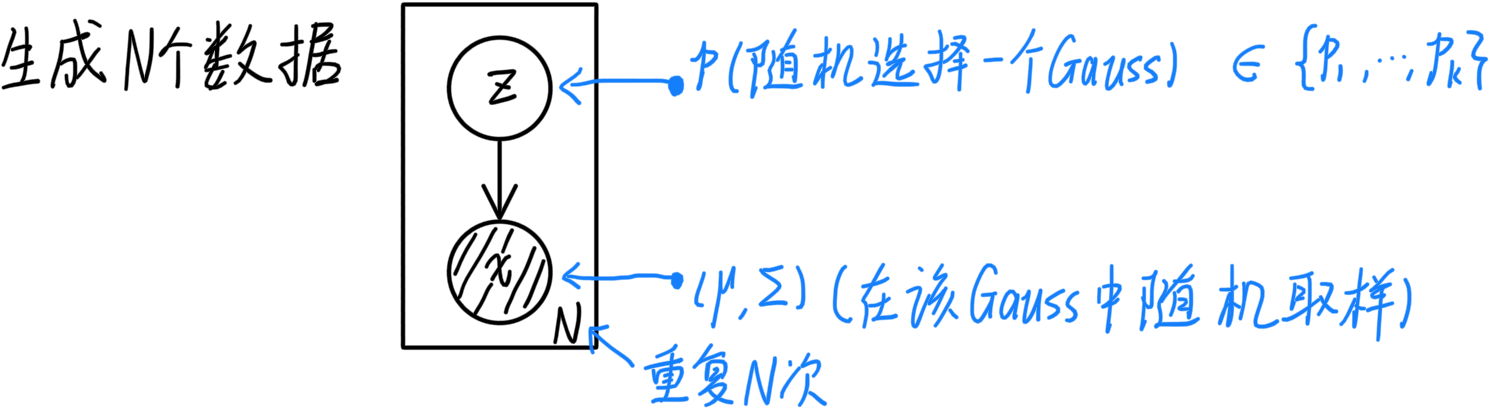
从概率图的角度看,GMM是概率生成模型,可以从隐变量的分布中生成N个数据,如下图:
11.2 通过MLE估计参数
首先简单的导出一下GMM的公式(核心思想就是引入 z z z):
P ( x ) = ∑ i = 1 K P ( x , z = C i ) = ∑ i = 1 K P ( x , z = C i ) = ∑ i = 1 K P ( z = C i ) P ( x ∣ z = C i ) = ∑ i = 1 K p i ⋅ N ( x ∣ μ i , Σ i ) P(x) = \sum_{i=1}^K P(x, z = C_i) = \sum_{i=1}^K P(x, z = C_i) = \sum_{i=1}^K P(z=C_i)P(x|z = C_i )= \sum_{i=1}^K p_i \cdot N(x|\mu_i, \Sigma_i) P(x)=i=1∑KP(x,z=Ci)=i=1∑KP(x,z=Ci)=i=1∑KP(z=Ci)P(x∣z=Ci)=i=1∑Kpi⋅N(x∣μi,Σi)
假设我们直接用MLE去进行参数求解,有:
θ ^ M L E = a r g max θ log P ( X ) = a r g max θ ∑ i = 1 N log P ( x i ) = a r g max θ ∑ i = 1 N log ∑ j = 1 K p j ⋅ N ( x i ∣ μ j , Σ j ) \begin{align} {\hat \theta}_{MLE} & = arg\max_{\theta} \log P(X) \\ & = arg\max_\theta \sum_{i=1}^N \log P(x_i) \\ & = arg\max_\theta \sum_{i=1}^N \log \sum_{j=1}^K p_j \cdot N(x_i|\mu_j, \Sigma_j) \end{align} θ^MLE=argθmaxlogP(X)=argθmaxi=1∑NlogP(xi)=argθmaxi=1∑Nlogj=1∑Kpj⋅N(xi∣μj,Σj)
我们发现公式中的对数还嵌套了累加运算,导致无法通过MLE求的解析解。
11.3 EM求解
由于无法求的解析解,我们只能通过近似方法求的近似解,通过GMM的性质,我们可以代入EM公式:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9UOSavbJ-1686302925549)(assets/11 GMM——高斯混合模型/image-20230606192743051.png)]](https://img-blog.csdnimg.cn/f81f906074d74d45b9d9fb24621d52e0.png)