1. 两数之和

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 的那两个整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

2 <= nums.length <= 103
-10^9 <= nums[i] <= 10^9
-10^9 <= target <= 10^9
只会存在一个有效答案

代码 1：

def twoSum(nums, target):cache = {}i = 0while i < len(nums):right = target-nums[i]if cache.get(right) is not None:return [cache[right], i]else:cache[nums[i]] = ii += 1return []# %%
print(twoSum([2,7,11,15], 9))
print(twoSum([3,2,4], 6))
print(twoSum([3,3], 6))

代码 2：

def twoSum(nums, target):cache = {}for i, value in enumerate(nums):if target - value not in cache:cache[nums[i]] = ielse:return [cache[target - nums[i]],i]# %%
print(twoSum([2,7,11,15], 9))
print(twoSum([3,2,4], 6))
print(twoSum([3,3], 6))

输出：

[0, 1]
[1, 2]
[0, 1]

2. 组合总和

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。
解集不能包含重复的组合。

示例 1：

输入：candidates = [2,3,6,7], target = 7,
输出：[[7],[2,2,3]]

示例 2：

输入：candidates = [2,3,5], target = 8,
输出：[[2,2,2,2],[2,3,3],[3,5]]

提示：

1 <= candidates.length <= 30
1 <= candidates[i] <= 200
candidate 中的每个元素都是独一无二的。
1 <= target <= 500

代码：

class Solution(object):def combinationSum(self, candidates, target):candidates.sort()dp = [[] for _ in range(target + 1)]dp[0].append([])for i in range(1, target + 1):for j in range(len(candidates)):if candidates[j] > i:breakfor k in range(len(dp[i - candidates[j]])):temp = dp[i - candidates[j]][k][:]if len(temp) > 0 and temp[-1] > candidates[j]:continuetemp.append(candidates[j])dp[i].append(temp)return dp[target]if __name__ == '__main__':s = Solution()print (s.combinationSum([8,7,4,3], 11))print (s.combinationSum([2,3,6,7], 7))print (s.combinationSum([2,3,5], 8))

输出：

[[3, 4, 4], [4, 7], [3, 8]]
[[2, 2, 3], [7]]
[[2, 2, 2, 2], [2, 3, 3], [3, 5]]

3. 相同的树

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。

如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

示例 1：

输入：p = [1,2,3], q = [1,2,3]
输出：true

示例 2：

输入：p = [1,2], q = [1,null,2]
输出：false

示例 3：

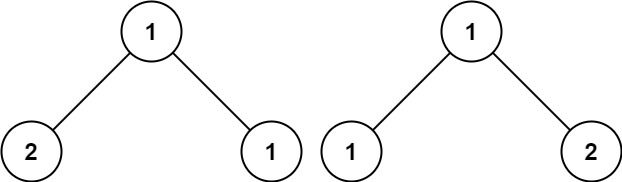
输入：p = [1,2,1], q = [1,1,2]
输出：false

提示：

两棵树上的节点数目都在范围 [0, 100] 内
-10^4 <= Node.val <= 10^4

代码：

class TreeNode(object):def __init__(self, x):self.val = xself.left = Noneself.right = Noneclass Solution(object):def isSameTree(self, p, q):""":type p: TreeNode:type q: TreeNode:rtype: bool"""if p == q:return Truetry:left = right = Trueif p.val == q.val:left = self.isSameTree(p.left, q.left)right = self.isSameTree(p.right, q.right)return (left and right)except:return Falsereturn False# %%
s = Solution()
print(s.isSameTree(p = [1,2,3], q = [1,2,3]))print(s.isSameTree(p = [1,2], q = [1,None,2]))
print(s.isSameTree(p = [1,2,1], q = [1,1,2]))

输出：

True
False
False

附录

二叉树

（Binarytree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个节点最多只能有两棵子树，且有左右之分。
二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个节点。

二叉树（binarytree）是指树中节点的度不大于2的有序树，它是一种最简单且最重要的树。二叉树的递归定义为：二叉树是一棵空树，或者是一棵由一个根节点和两棵互不相交的，分别称作根的左子树和右子树组成的非空树；左子树和右子树又同样都是二叉树。

二叉树是递归定义的，其节点有左右子树之分，逻辑上二叉树有五种基本形态：
1、空二叉树；2、只有一个根节点的二叉树；3、只有左子树；4、只有右子树；5、完全二叉树。

常用术语

①节点：包含一个数据元素及若干指向子树分支的信息。
②节点的度：一个节点拥有子树的数目称为节点的度。
③叶子节点：也称为终端节点，没有子树的节点或者度为零的节点。
④分支节点：也称为非终端节点，度不为零的节点称为非终端节点。
⑤树的度：树中所有节点的度的最大值。
⑥节点的层次：从根节点开始，假设根节点为第1层，根节点的子节点为第2层，依此类推，如果某一个节点位于第L层，则其子节点位于第L+1层。
⑦树的深度：也称为树的高度，树中所有节点的层次最大值称为树的深度。
⑧有序树：如果树中各棵子树的次序是有先后次序，则称该树为有序树。
⑨无序树：如果树中各棵子树的次序没有先后次序，则称该树为无序树。
⑩森林：由m（m≥0）棵互不相交的树构成一片森林。如果把一棵非空的树的根节点删除，则该树就变成了一片森林，森林中的树由原来根节点的各棵子树构成。