5 最小生成树

  构造连通网的最小代价生成树称为最小生成树，即Minimum Cost Spanning Tree，最小生成树通常是基于无向网/有向网构造的。

  找连通网的最小生成树，经典的有两种算法，普里姆算法和克鲁斯卡尔算法。

5.1 普里姆（Prim）算法

  普里姆算法，即Prim算法，大致实现过程如下：

  (1) 新建数组adjVex[n]，初始值均为0；新建数组lowCost[n]，初始值均为infinity；

  (2) 从第一个顶点X（下标为0）开始，把它与各顶点连接的权记录下来，放到lowCost数组里面，然后找到权最小的那个顶点Y，得到最小生成树的第一条边(X,Y)，然后把lowCost数组里面Y对应的下标的元素设置为0；

  (3) 然后处理顶点Y，把它与除X外的其他各顶点连接的权，与lowCost数组下标相同的权比较，将小的放入到lowCost里面，并把较小的权对应的顶点的下标记录在adjVex数组里面，也即，adjVex[j]要么是Y，要么是除X外的其他顶点；

  (4) 找到lowCost数组中权最小的那个（显然不会是X，也不会是Y），得到最小生成树的第二条边(adjVex[j],j)，然后把lowCost[j]设置为0；

  (5) 然后按(3)、(4)的规则，处理第j个顶点，直到所有顶点都被连接起来（注意，最小连通树是针对连通网的）；

  下面我们会根据各种存储方式进行举例。

5.1.1 邻接矩阵的最小生成树

  假设有以下无向网：

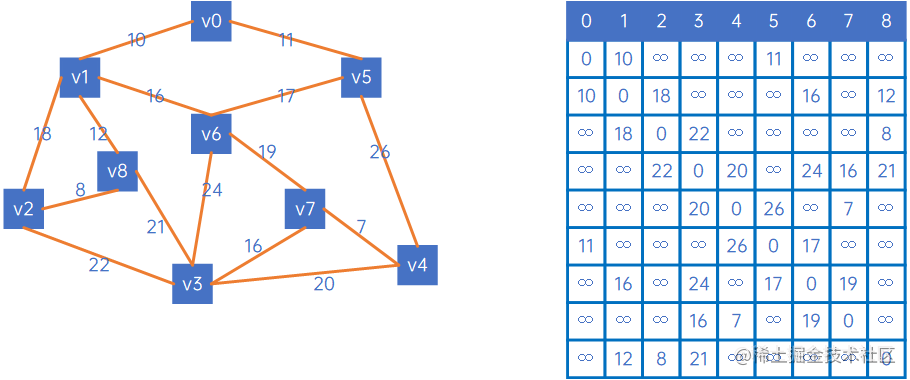
  我们定义两个数组，一个X={}，Y={V0、v1、v2、v3、v4、v5、v6、v7、v8}，其中X表示已连通的顶点，Y表示未连通的顶点。

  先从第一个顶点v0开始，把它加入X，表示已连通，这时，X={v0}，Y={v1、v2、v3、v4、v5、v6、v7、v8}。

  接下来，看X中的V0与其他顶点关联时权值情况，发现(v0,v1)的权值最小，因此认为，v0和v1是最小生成树的一个边，此时X={v0、v1}，Y={v2、v3、v4、v5、v6、v7、v8}：

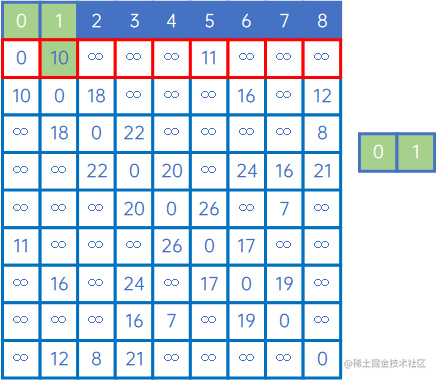
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V0,v5)之间的权值最小，因此认为(V0,v5)是最小生成树的一条边，此时X={v0、v1、v5}，Y={v2、v3、v4、v6、v7、v8}：

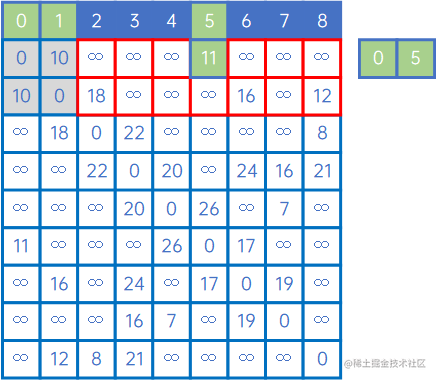
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V1,v8)之间的权值最小，因此认为(V1,v8)是最小生成树的一条边，此时X={v0、v1、v5、v8}，Y={v2、v3、v4、v6、v7}：

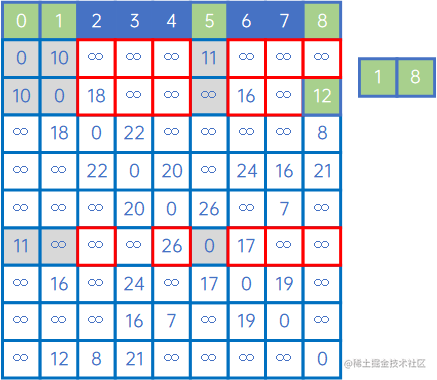
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V8,v2)之间的权值最小，因此认为(V8,v2)是最小生成树的一条边，此时X={v0、v1、v5、v8、v2}，Y={v3、v4、v6、v7}：

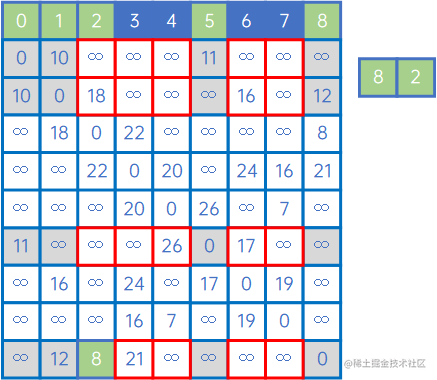
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V1,v6)之间的权值最小，因此认为(V1,v6)是最小生成树的一条边，此时X={v0、v1、v5、v8、v2、v6}，Y={v3、v4、v7}：

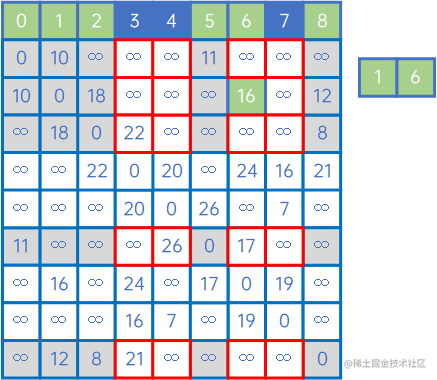
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V6,v7)之间的权值最小，因此认为(V6,v7)是最小生成树的一条边，此时X={v0、v1、v5、v8、v2、v6、v7}，Y={v3、v4}：

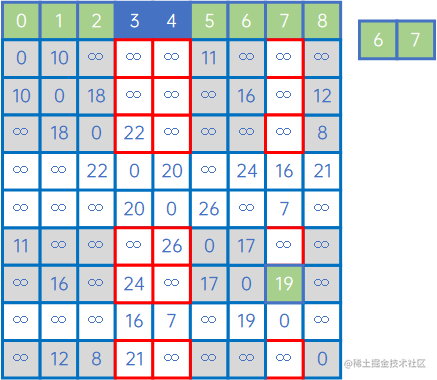
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V7,v4)之间的权值最小，因此认为(V7,v4)是最小生成树的一条边，此时X={v0、v1、v5、v8、v2、v6、v7、v4}，Y={v3}：

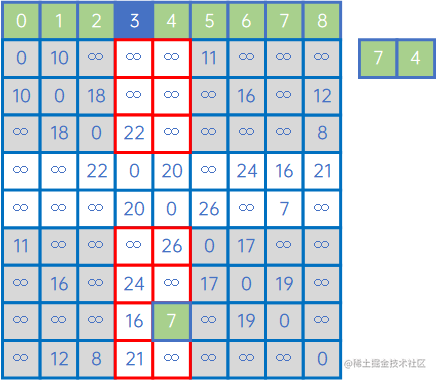
  然后，再看X中的所有顶点与Y中的所有顶点的权值，发现边现(V7,v3)之间的权值最小，因此认为(V7,v3)是最小生成树的一条边，此时X={v0、v1、v5、v8、v2、v6、v7、v4、v3}，Y={}：

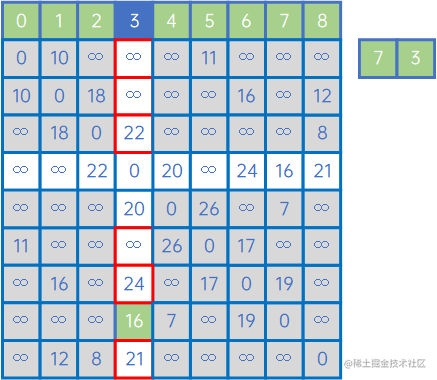
  这时，Y已处理完毕，所有顶点都连起来了，形成了最小生成树。

  观察一下，我们在获取最小生成树的边时，第一步是从arc[0][j]取权最小的，取到了(v0,v1)，第二步，是从arc[0][j]和arc[1][j]中取权值最小的，取到了(v0,v5)，第三步，是从arc[0][j]、arc[1][j]和arc[5][j]中取权最小的，取到了(v1,v8)，也即，规则是：

  (1) 从arc[0][j]中取最小权对应的边(v0,v1)，此时X={v0}，把v1加入到X中；

  (2) 从arc[0][j]、arc[1][j]中取最小权对应的边(v0,v5)，此时X={v0,v1}，把v5加入到X中；

  (3) 从arc[0][j]、arc[1][j]、arc[5][j]中取最小权对应的边(v1,v8)，此时X={v0,v1,v5}，把v8加入到X中；

  (4) 从arc[0][j]、arc[1][j]、arc[5][j]…arc[x][j]中取最小权对应的边(vi,vk)，然后判断vi和vk是否在X中，不在则加入到X中；

  当在arc[0][j]、arc[1][j]、arc[5][j]…arc[x][j]中取最小的权时，我们要比较x个一元数组的值，我们再做一下优化：

  (1) 从arc[0][j]中取最小权对应的边(v0,v1)，此时X={v0}，把v1加入到X中；

  (2) 从arc[0][j]、arc[1][j]中取最小权对应的边(v0,v5)，此时X={v0,v1}，把v5加入到X中，然后我们把arc[0][j]、arc[1][j]组合一下，取出arc[0][j]、arc[1][j]中较小的权放到lowCost[j]里面，同时使用一个数组adjVex[j]记录lowCost[j]对应的起始顶点下标，同时标注lowCost[0]、lowCost[1]的值为负无穷大，如下：

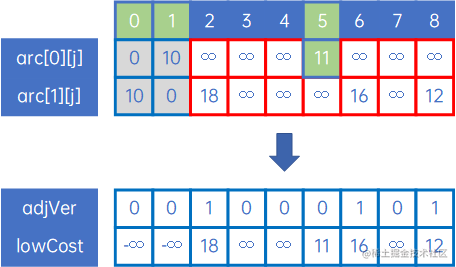
  (3) 这时，只需要从lowCost[j]、arc[5][j]中取最小权对应的边就行了，不用再迭代arc[0][j]和arc[1][j]；

  因此，我们定义两个数组，lowCost[n]表示已处理过的顶点跟其他顶点之间的权值最小值列表，其中已处理过的顶点之间的权值设置为负无穷大，adjVex[n]表示最小权值对应的起始顶点，我们重新来看看上述无向网。

  第一步，定义lowCost[n]和adjVex[n]，adjVex[n]默认值为0，lowCost[n]默认值为负无穷大：

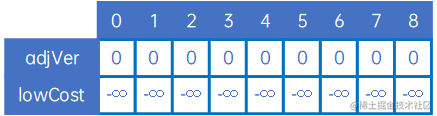
  接下来处理第一个顶点，找到第一个顶点与其他顶点中权值最小的那条边（自身除外），具体做法是，令adjVex[n]的元素均为0，令lowCost[n]的元素值为arc[0][j]，然后找到权值最小的arc[0][x]，取边(adjVex[x],x)，即(v0,v1)：

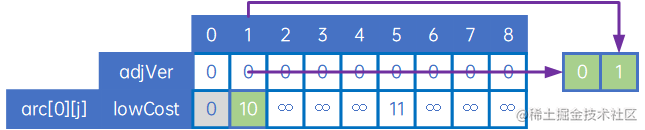
  接下来，要比较的应是arc[0][j]和arc[1][j]中，除arc[0][0]、arc[0][1]、arc[1][0]和arc[1][1]外的其他值，取最小值，因为我们要取的是“其他顶点与顶点v0、v1中权值最小的边”，因此我们把arc[1][j]与lowCost[n]（这时，lowCost即为arc[0][j]）比较，把较小的写入到lowCost中，同时把较小权对应对应的顶点下标写入到adjVex[n]中，如下：

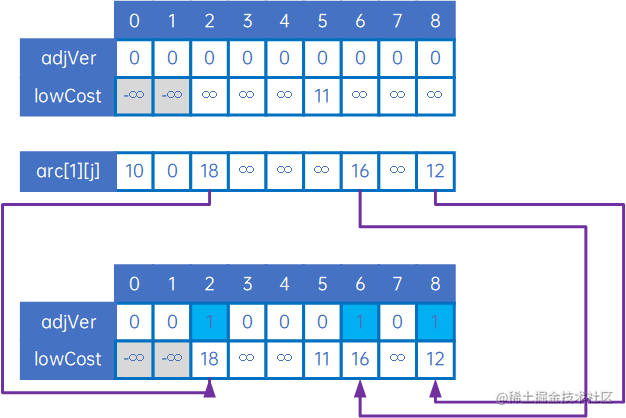
  如上可知，arc[1][2]小于lowCost[2]，因此令lowCost[2]=arc[1][2]、adjVex[2]=1，arc[1][6]和arc[1][8]也相似处理。

  然后，我们取出其中的最小权，得到下一条最小生成树的边，即(v0,v5)：

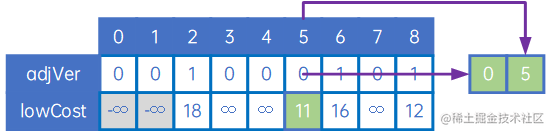
  接下来，是取得顶点v0、v1、v5与其他顶点的权中的最小值，生成下一条边，整体处理方式与上文类似：

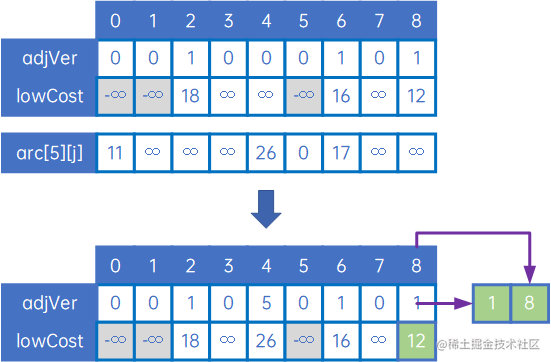
  后续操作也类似，直到所有顶点处理完毕，得到最小生成树。

  让我们来看有向网的处理，按上述过程处理，得到以下结果：

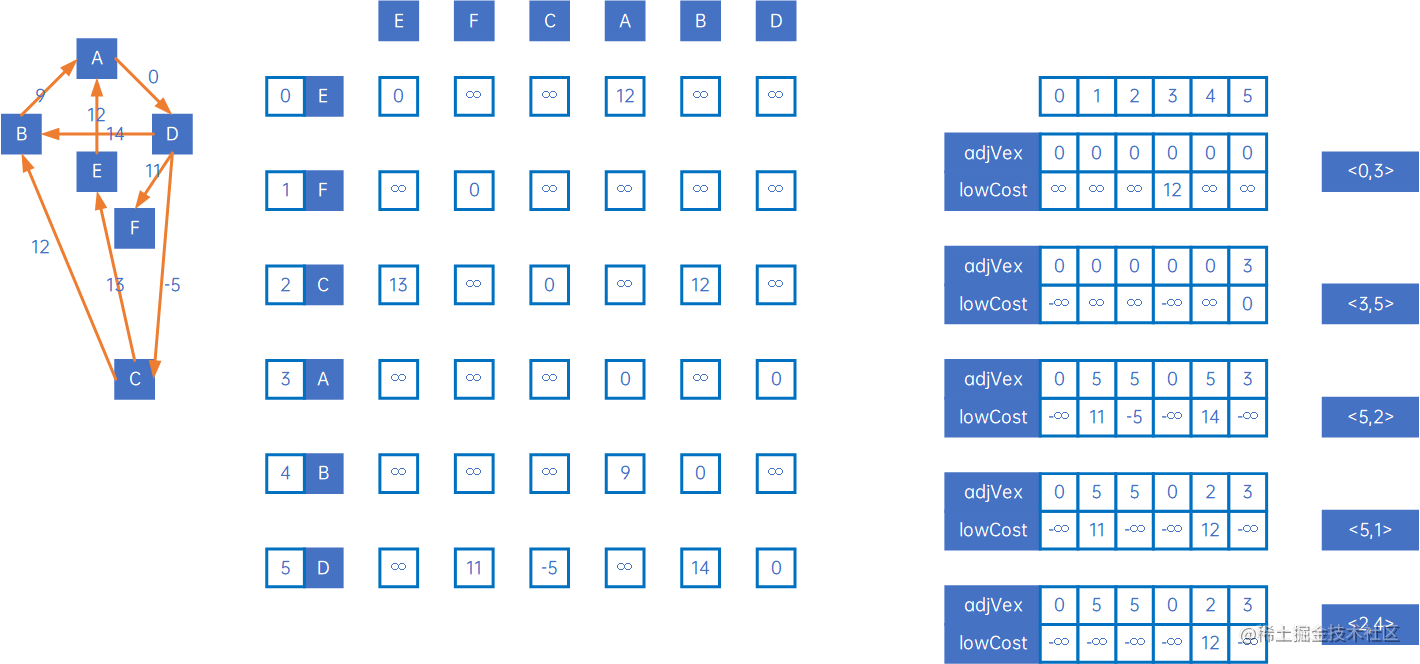
  即：

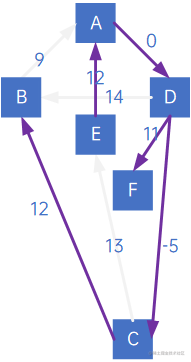
  但注意观察，同样是连通B顶点，弧<B,A>实际上比<C,B>权小，所以最小生成树应该为：

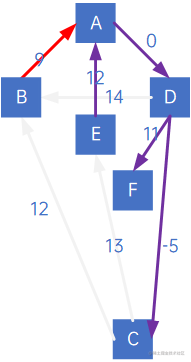
  因此，有向树的最小生成树生成过程中，不仅要看“顶点X指向的顶点中权最小的”，还要看“顶点X被指向的顶点中权最小的”。

  因此，寻找最低代码的边/弧的逻辑应是“找到该顶点指向的即该顶点被指向的顶点中，代价最小的边或弧”，对于无向网当然这两个概念是一样的，但对于有向网，则要进行双向处理，因此上述有向网的处理逻辑有所不同。

  以以上有向网为例，第一步，定义三个数组：lowCost与无向网相同，tailVex和headVex代替adjVex，分别表示箭头的尾巴和头（若为无向网则尾巴和头可以任意），初始化tailVex和headVex为0，lowCost为无穷大：

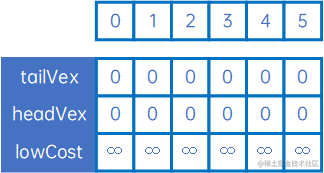
  然后使用arc[0][j]和arc[j][0]与lowCost比较，取小的权，并记录箭头的尾巴和头，可取出最小的权对应的尾巴和头，得到最小生成树的第一条弧<0,3>，然后设置lowCost[0]和lowCost[3]为负无穷大，表示这两个顶点已连通：

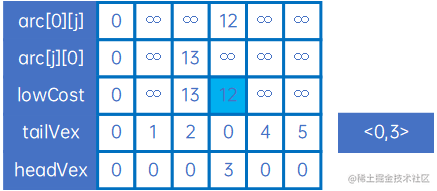
  然后取arc[3][j]和arc[j][3]，重复上述处理，得到下一条弧<3,5>，然后设置lowCost[3]和lowCost[5]为负无穷大，表示这两个顶点已连通：

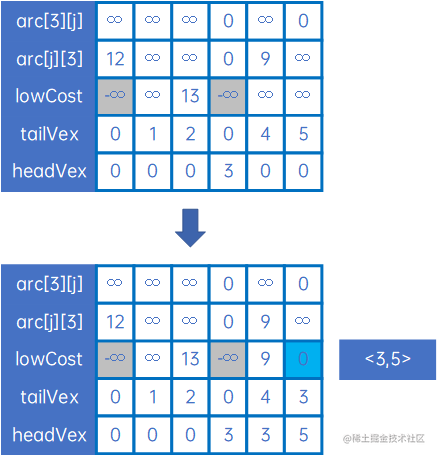
  然后对arc[5][j]和arc[j][5]做类似处理，一直到所有顶点都连通。

  代码实现如下所示：

/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点tailVex[j]到顶点headVex[j]的权W(adj[j],j)”中较优（如果是数值的话就是较小）的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];// 取权最小的，即第一个顶点与其他顶点之间权最小的顶点int index = 0;int connectedNum = 0;boolean[] visited = new boolean[vertexNum];while (connectedNum < vertexNum) {// 其他顶点是与lowCost比较，取小的W minWeight = null;int newIndex = index;for (int i = 0; i < vertexNum; i++) {if (i != index && !lowCost[i].equals(visitedVal) && arc[index][i].compareTo(lowCost[i]) < 0) {lowCost[i] = arc[index][i];tailVex[i] = index;headVex[i] = i;}if (type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED_NETWORK)) {// 有向网还需要处理指向本顶点的顶点if (i != index && !lowCost[i].equals(visitedVal) && arc[i][index].compareTo(lowCost[i]) < 0) {lowCost[i] = arc[i][index];tailVex[i] = i;headVex[i] = index;}}// 取出最小的权// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];newIndex = i;}}}index = newIndex;// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;}return result;}

5.1.2 邻接表的最小生成树

  邻接表和逆邻接表的处理方式也是类似，只是需要找到指向的和被指向的顶点的权进行比较，另外，邻接表和逆邻接表的处理方式也会有差异：

/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优（如果是数值的话就是较小）的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {for (int i = 0; i < vertexNum; i++) {VertexNode<T, W> vertexNode = vertexes[i];EdgeNode<W> edgeNode = vertexNode.getFirstEdge();while (null != edgeNode) {int refIndex = edgeNode.getIndex();W weight = edgeNode.getWeight();// 邻接表if (i == index && !lowCost[refIndex].equals(visitedVal) &&weight.compareTo(lowCost[refIndex]) < 0) {// 本顶点指向的if (!reverseAdjacency) {tailVex[refIndex] = i;headVex[refIndex] = refIndex;lowCost[refIndex] = weight;} else {tailVex[refIndex] = refIndex;headVex[refIndex] = i;lowCost[refIndex] = weight;}} else if (refIndex == index && !lowCost[i].equals(visitedVal) &&weight.compareTo(lowCost[i]) < 0) {if (!reverseAdjacency) {// 指向本顶点的tailVex[i] = i;headVex[i] = refIndex;lowCost[i] = weight;} else {tailVex[i] = refIndex;headVex[i] = i;lowCost[i] = weight;}}edgeNode = edgeNode.getNext();}}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}

5.1.3 十字链表的最小生成树

  十字链表记录了每个顶点的in和out，因此十字链表的处理较为简单。

/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优（如果是数值的话就是较小）的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {AcrossLinkVertexNode<T, W> vertexNode = vertexes[index];// 处理指向自己的AcrossLinkEdgeNode<W> inEdge = vertexNode.getFirstIn();while (null != inEdge) {// 自身是headint tailIndex = inEdge.getTailIndex();W weight = inEdge.getWeight();if (!lowCost[tailIndex].equals(visitedVal) && weight.compareTo(lowCost[tailIndex]) < 0) {lowCost[tailIndex] = weight;tailVex[tailIndex] = tailIndex;headVex[tailIndex] = index;}inEdge = inEdge.getNextTail();}// 处理指向的AcrossLinkEdgeNode<W> outEdge = vertexNode.getFirstOut();while (null != outEdge) {// 自身是tailint headIndex = outEdge.getHeadIndex();W weight = outEdge.getWeight();if (!lowCost[headIndex].equals(visitedVal) && weight.compareTo(lowCost[headIndex]) < 0) {lowCost[headIndex] = weight;tailVex[headIndex] = index;headVex[headIndex] = headIndex;}outEdge = outEdge.getNextHead();}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}

5.1.4 邻接多重表的最小生成树

  邻接多重表是对无向网的优化，因此我们不考虑有向网，而在无向网中，通过iVex、iLink、jVex、jLink，可以直接定位到某顶点关联的所有顶点，因此代码实现如下所示：

/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED_NETWORK)) {// 最小生成树只针对无向网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优（如果是数值的话就是较小）的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {AdjacencyMultiVertexNode<T, W> vertexNode = vertexes[index];AdjacencyMultiEdgeNode<W> edgeNode = vertexNode.getFirstEdge();boolean firstEdge = true;while (null != edgeNode) {int refIndex = index;int iVex = edgeNode.getIVex();int jVex = edgeNode.getJVex();W weight = edgeNode.getWeight();if (firstEdge) {refIndex = jVex;edgeNode = edgeNode.getILink();firstEdge = false;} else {if (iVex == index) {refIndex = jVex;} else if (jVex == index) {refIndex = iVex;}edgeNode = edgeNode.getJLink();}if (!lowCost[refIndex].equals(visitedVal) && weight.compareTo(lowCost[refIndex]) < 0) {lowCost[refIndex] = weight;tailVex[refIndex] = iVex;headVex[refIndex] = jVex;}}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}

5.5.5 边集数组的最小生成树

  边集数组的最小生成树实现代码如下所示：

/*** 生成最小生成树** @param visitedVal 已访问的顶点被标记的值* @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-07 15:23:14**/
@SuppressWarnings("unchecked")
public List<String> minimumCostSpanningTree(W visitedVal) {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 用于存储“当前检查的顶点X与顶点j的权W(X,j)”及“顶点adjVex[j]到顶点j的权W(adj[j],j)”中较优（如果是数值的话就是较小）的那个权W[] lowCost = (W[]) Array.newInstance(infinity.getClass(), vertexNum);for (int i = 0; i < vertexNum; i++) {lowCost[i] = infinity;}// 用于存储箭头的尾和头int[] tailVex = new int[vertexNum];int[] headVex = new int[vertexNum];boolean[] visited = new boolean[vertexNum];int connectedNum = 0;int index = 0;while (connectedNum < vertexNum) {for (int i = 0; i < edgeNum; i++) {EdgeListEdgeNode<W> edgeNode = arc[i];int begin = edgeNode.getBegin();int end = edgeNode.getEnd();W weight = edgeNode.getWeight();if (begin == index && !lowCost[end].equals(visitedVal) && weight.compareTo(lowCost[end]) < 0) {lowCost[end] = weight;tailVex[end] = begin;headVex[end] = end;} else if (end == index && !lowCost[begin].equals(visitedVal) && weight.compareTo(lowCost[begin]) < 0) {lowCost[begin] = weight;tailVex[begin] = begin;headVex[begin] = end;}}// 取lowCost中最小的那个W minWeight = null;for (int i = 0; i < vertexNum; i++) {// 忽略自身// 忽略lowCost[j]为已访问过的顶点if (i != index && !lowCost[i].equals(visitedVal)) {if (null == minWeight || minWeight.compareTo(lowCost[i]) > 0) {minWeight = lowCost[i];index = i;}}}// 打印取到的边switch (type) {case DIRECTED_NETWORK: {String val = "<" + tailVex[index] + "," + headVex[index] + ">";result.add(val);// 用于测试System.out.println(val);break;}case UNDIRECTED_NETWORK: {String val = "(" + tailVex[index] + "," + headVex[index] + ")";result.add(val);// 用于测试System.out.println(val);break;}}// 设置已连通的顶点数if (!visited[tailVex[index]]) {visited[tailVex[index]] = true;connectedNum++;}// 设置该顶点已处理if (!visited[headVex[index]]) {visited[headVex[index]] = true;connectedNum++;}// 设置lowCost[index]为已访问lowCost[tailVex[index]] = visitedVal;lowCost[headVex[index]] = visitedVal;// 用于测试StringBuilder builder = new StringBuilder("lowCost is [");StringBuilder builder2 = new StringBuilder("tailVex is [");StringBuilder builder3 = new StringBuilder("headVex is [");for (int i = 0; i < vertexNum; i++) {builder.append(lowCost[i]).append(",");builder2.append(tailVex[i]).append(",");builder3.append(headVex[i]).append(",");}builder.append("]");builder2.append("]");System.out.println(builder);System.out.println(builder2);System.out.println(builder3);}return result;}

5.2 克鲁斯卡尔(Kruskal)算法

  克鲁斯卡尔的官方描述是“假设N=(V,{E})是连通网，则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{})，图中每个顶点自成一个连通分量。在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边选择下一条代价最小的边。依此类推，直到T中所有顶点都在同一连通分量上为止”。

  克鲁斯卡尔算法针对的是边，因此我们用边集数组来进行克鲁斯卡尔算法的实现描述，以以下边集数组为例：

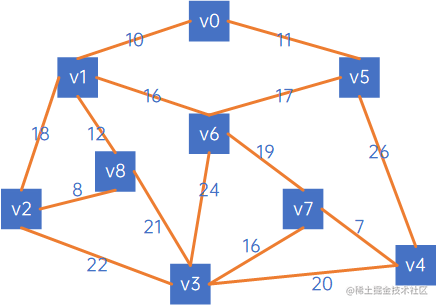
  首先我们定义一个数组connected来存储已连通的分量，长度为顶点长度，默认值均为无穷大，表示所有顶点均为连通：

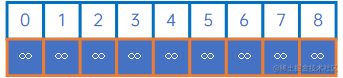
  这里面的规则是：如果connected[i]=j,connected[j]=x,connected[x]=$\infty$，则表示顶点i、j、x是连通的。

  然后我们把边集数组按权由小到大排序：

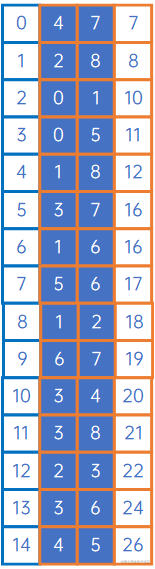
  迭代边集数组，首先是arc[0]，begin=4，end=7，connected[4]=$\infty$，connected[7]=$\infty$，这两个顶点未连通，我们把它们连通起来，输出第一个连通分量的第一条边(4,7)，同时令connected[4]=7，表示这两个顶点已连通：

  然后是arc[1]，begin=2，end=8，connected[2]=$\infty$，connected[8]=$\infty$，这两个顶点未连通，我们把它们连通起来，输出第二个连通分量的第一条边(2,8)，同时令connected[2]=8，表示这两个顶点已连通：

  后续arc[2]处理方式同上：

  然后看arc[3]，begin=0，end=5，注意到，connected[0]=1，表示第0和第1个顶点是已经连通的，第0个顶点已在一个连通分量内，我们继续看这个连通分量里面有哪些顶点：connected[0]=1，connected[1]=$\infty$，按上面定的规则，表示这个连通分量里面只有0和1两个顶点；connected[5]=$\infty$，表示顶点5没有在任何一个连通分量内，这时，我们令connected[1]=5，表示顶点0、1、5在同一个连通分量内，并输出(0,5)，表示这个边是这个连通分量的一条边：

  然后看arc[4]，begin=1，end=8，因connected[1]=5，connected[5]=0，connected[8]=$\infty$，表示顶点1和顶点5在同一个连通分量内，但这个连通分量不包含顶点8，因此令connected[5]=8，并输出边(1,8)，将顶点8也加入到这个连通分量内：

  接下来arc[5]和arc[6]的处理方式类似：

  来看arc[7]，begin=5，end=6，此时，connected[5]=8，connected[8]=6，connected[6]=0，即顶点5、8、6在一个连通分量内，即begin和end都在一个连通分量内，不需要处理，跳过。

  arc[8]与arc[7]一致，相关顶点都在同一个连通分量内，不需要处理，跳过。

  继续迭代arc，按如上规则处理，能得到最终的最小生成树。

  代码实现如下所示：

/*** 生成最小生成树，克鲁斯卡尔算法** @return 最小生成树的边或弧列表* @author Korbin* @date 2023-02-13 15:09:58**/
public List<String> minimumCostSpanningTree() {List<String> result = new ArrayList<>();if (type.equals(BusinessConstants.GRAPH_TYPE.UNDIRECTED) ||type.equals(BusinessConstants.GRAPH_TYPE.DIRECTED)) {// 最小生成树只针对网return null;}// 对边集数组按权从小到大进行排序sortArc(0, edgeNum);// 定义一个数组，并初始化为infinity，用于表示连通分量int[] connected = new int[vertexNum];for (int i = 0; i < vertexNum; i++) {connected[i] = -1;}// 迭代边集数组for (int i = 0; i < edgeNum; i++) {EdgeListEdgeNode<W> edgeNode = arc[i];int begin = edgeNode.getBegin();int end = edgeNode.getEnd();// 寻找begin对应的连通分量int beginComponent = begin;while (connected[beginComponent] != -1) {beginComponent = connected[beginComponent];}// 寻找end对应的连通分量int endComponent = end;while (connected[endComponent] != -1) {endComponent = connected[endComponent];}// 如果不在同一个连通分量if (beginComponent != endComponent) {connected[beginComponent] = end;switch (type) {case UNDIRECTED_NETWORK: {String val = "(" + begin + "," + end + ")";result.add(val);break;}case DIRECTED_NETWORK: {String val = "<" + begin + "," + end + ">";result.add(val);break;}}}}return result;
}

5.3 总结

  普里姆（Prim）算法，从一个顶点出发X，取其他所有顶点与X连通的权中最小权对应的那个顶点Y，放入连通分量TE中，然后取其他所有顶点与X和Y连通的权中最小权对应的那个顶点Z，放入连通分量中，直到所有的顶点都在连通分量中时，最小生成树生成。

  克鲁斯卡尔（Kruskal）算法，把所有的边放到一个数组中，按权从小到大排序，然后从第一条边开始迭代，判断begin和end是否在同一个连通分量，若不在，则把他们连通起来，直到所有边都处理完毕。

  相对来讲，克鲁斯卡算法更适用于边集数组，而普里姆虽然各类存储结构都可以实现，但时间复杂度不同：

存储结构	普里姆算法		克鲁斯卡尔算法
	适用性	最差时间复杂度	适用性	最差时间复杂度
邻接矩阵	适用	O(n2)	不适用	--
邻接表	适用	O(n3)	不适用	--
十字链表	适用	O(n2)	不适用	--
邻接多重表	适用	O(n2)	不适用	--
边集数组	适用	O(n2)	适用	O(nlog(n))

  注：本文为程 杰老师《大话数据结构》的读书笔记，其中一些示例和代码是笔者阅读后自行编制的。