画个球

不管篮球和不和鸡联系起来，都首先得有个球，或者说要有一个球面，用参数方程可以表示为

$$\begin{array}{rl}x& =r\cos \varphi \cos \theta \\ y& =r\cos \varphi \sin \theta \\ z& =r\sin \varphi \end{array}$$

当然，有球还不行，还得有篮球。篮球其实很好画，只要在球上加两个背带就可以了，这一点可以用Python来实现，但考虑到方便，还是用PS直接P了一下，希望最后画出来不是太离谱。

那么现在球有了，还必须得有鸡，所以在百度上找一只。然后把这只鸡映射到球面上。

接下来就是关键步骤，如何将这个平面卷成一个球？方法也很简单，只需进行颜色映射就行了。

import numpy as np
import matplotlib.pyplot as plt
path = "bracken1.jpg"
img = plt.imread(path)
#img = img[::5, ::5, :]
h, w, c = img.shape
ys, xs = np.indices([h, w])
th = xs/w*np.pi*2
phi = np.pi/2 - ys/h*np.pix = np.cos(phi)*np.cos(th)
y = np.cos(phi)*np.sin(th)
z = np.sin(phi)cs = [tuple(c/255) for c in img.reshape(-1,3)]
ax = plt.subplot(projection='3d')
ax.scatter(x, y, z, marker='.', c=cs)
plt.axis('off')
plt.show()

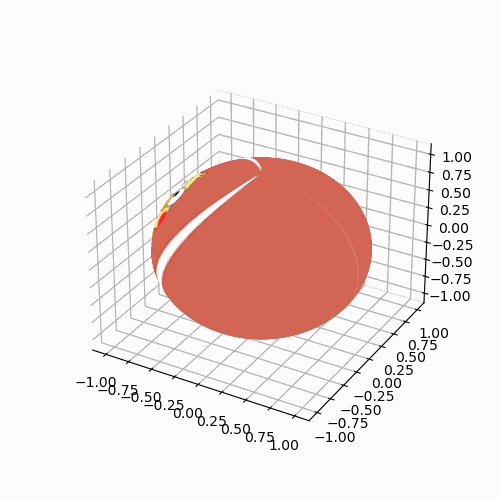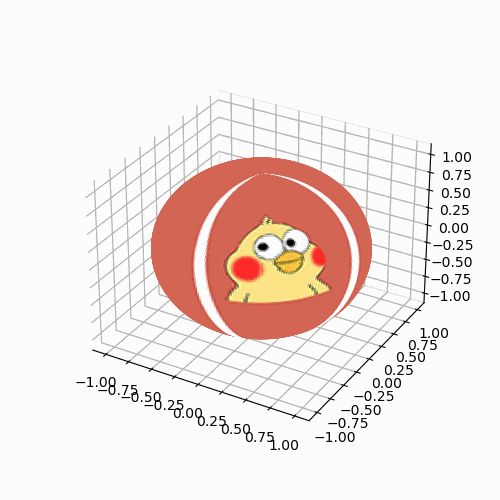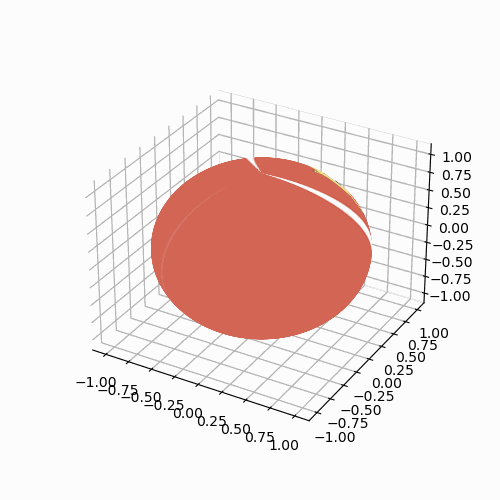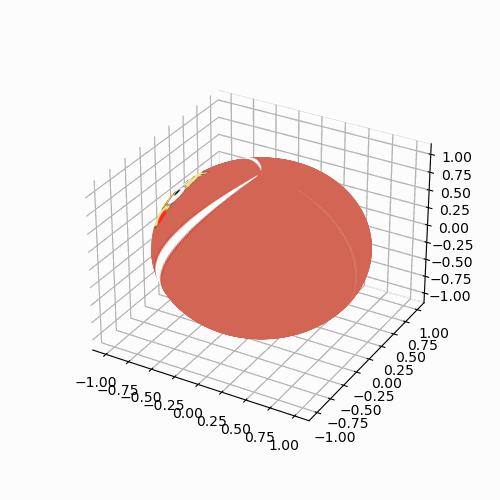
效果为

让球转起来

当然需要注意的一个是，这是个球，而不是一个圆，所以下面让这个球转一下。想要让球转动，那就得有一个旋转矩阵，三个方向的旋转矩阵如下表

$R_x(\theta )$	$R_x(\theta )$	$R_x(\theta )$
$\left[\begin{array}{ccc}1& 0& 0\\ 0& C_{\theta }& -S_{\theta }\\ 0& S_{\theta }& C_{\theta }\end{array}\right]$	$\left[\begin{array}{ccc}{C}_{\theta }& 0& S_{\theta }\\ 0& 1& 0\\ -S_{\theta }& 0& C_{\theta }\end{array}\right]$	$\left[\begin{array}{ccc}{C}_{\theta }& S_{\theta }& 0\\ -S_{\theta }& C_{\theta }& 0\\ 0& 0& 1\end{array}\right]$

由于只需绕Z轴转动，所以代码如下

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import animationcos = lambda th : np.cos(np.deg2rad(th))
sin = lambda th : np.sin(np.deg2rad(th))Rz = lambda th : np.array([[cos(th) , -sin(th), 0],[sin(th), cos(th), 0],[0       , 0,       1]])xyz = np.array([x,y,z]).reshape(3,-1)fig = plt.figure(figsize=(5,5))
ax = fig.add_subplot(projection='3d')
ax.grid()lines = ax.scatter(x, y, z, marker='.', c=cs)def animate(n):# 按照xyz顺序旋转axis = [2,1,0]shape = xyz.shapelines._offsets3d = Rz(n)@xyzreturn lines,ani = animation.FuncAnimation(fig, animate, range(0, 360, 2), interval=25, blit=True)#plt.show()
ani.save("zyx.gif")

效果如下，还挺有喜感的。