这里写目录标题
- 算法的复杂度
- 大O的渐进表示法
- 实例分析
- 空间复杂度
- 每日一题
算法的复杂度
衡量一个算法的好坏,一般 是从时间和空间两个维度来衡量的,
即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,
空间复杂度主要衡量一个算法运行所需要的额外空间
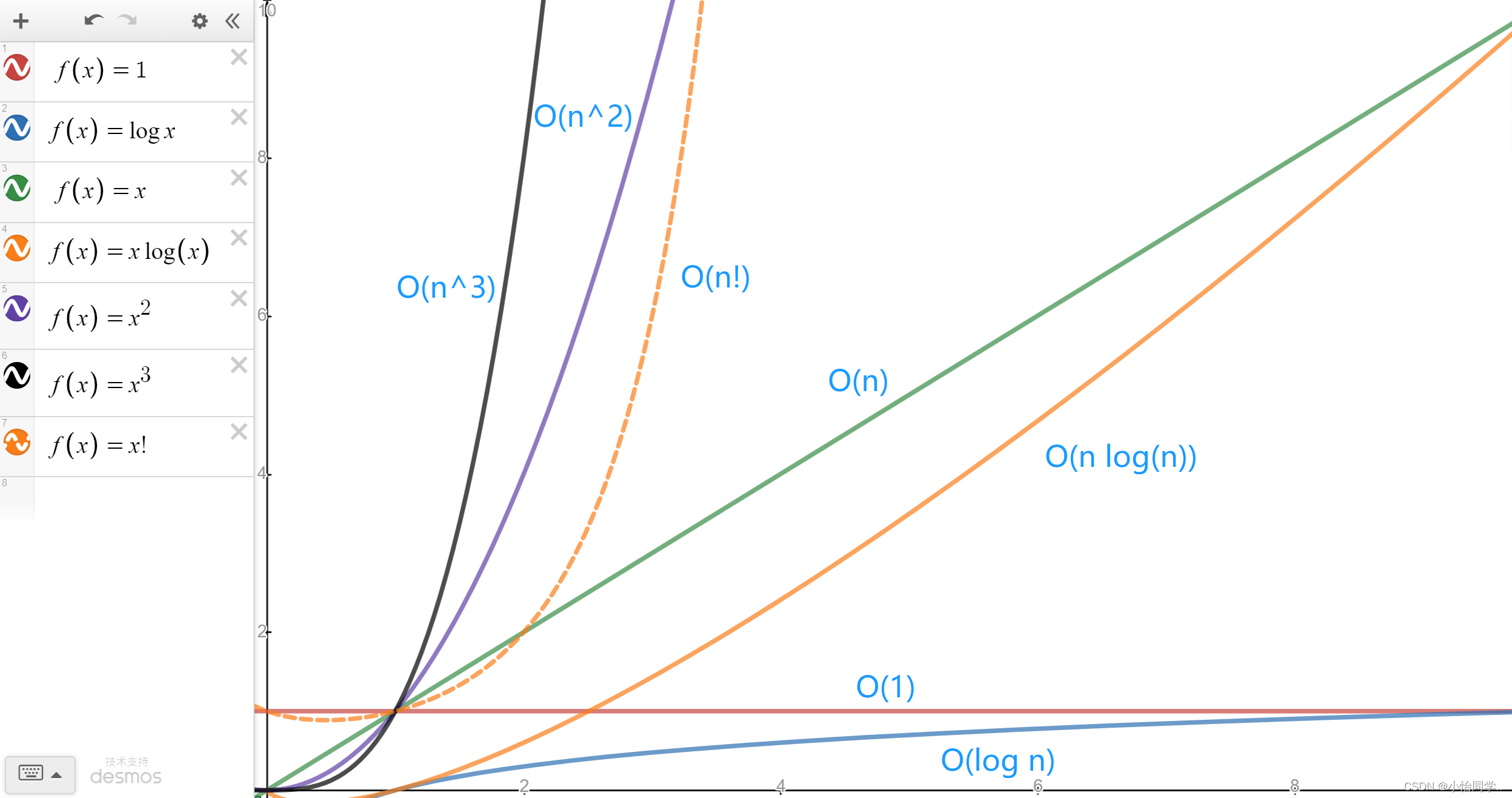
大O的渐进表示法
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。//一般是大O的渐进表达法是运算的最坏情况,而且最好不要通过代码中有几层循环来判断如: 2N+10 时间复杂度为O(N)
M+N 时间复杂度为O(M+N)
(N*(N+1)/2 时间复杂度为O(N^2)
实例分析
这是一个关于二分的编码 ,把总元素看作N ,每循环一次都会少去一半的元素,共循环(logN)次这里在算法中底数为二(有些地方是lgN),所以时间复杂度为O(logN)
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n-1;
while (begin <= end)
{
int mid = begin + ((end-begin)>>1);
if (a[mid] < x)
begin = mid+1;
else if (a[mid] > x)
end = mid-1;
else
return mid;
}
return -1;
}
这是关于斐波那契的递归 ,一个函数的时间复杂度为O(1),但是通过不断递归
如图所示所以时间复杂度为O(2^n)
long long Fib(size_t N)
{
if(N < 3)
return 1;
return Fib(N-1) + Fib(N-2);
}
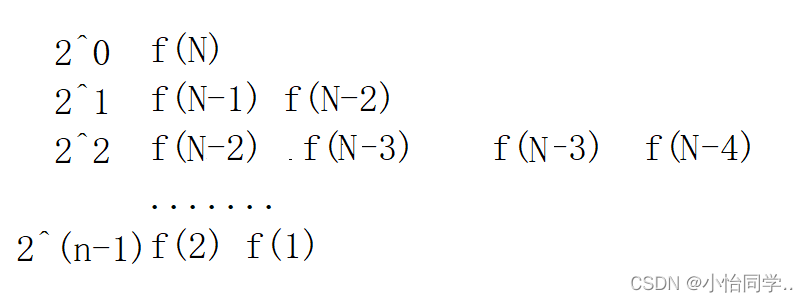
空间复杂度
空间复杂度大O渐进表示法来表示,主要是临时占用存储空间大小的量度
下列代码中主要开辟三个额外的变量,用大O表达式为O(1),因为代码中的数组是原本就有的,当函数被销毁时,函数的开辟的空间也不再存在
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{int exchange = 0;
for (size_t i = 1; i < end; ++i)
{if (a[i-1] > a[i])
{Swap(&a[i-1], &a[i]);exchange = 1;
}
}
if (exchange == 0)break;
}
}
如图所示 由递归思想可知每递归,递到最后时 往回归嘛,函数栈会销毁
如fibArray[2] 销毁时,fibArray[1]会使用这个被销毁的空间 所以以此类推
大O表达式为(N)
long long* Fibonacci(size_t n)
{
if(n==0)
return NULL;
long long * fibArray = (long long *)malloc((n+1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n ; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray [i - 2];
}
return fibArray;
}
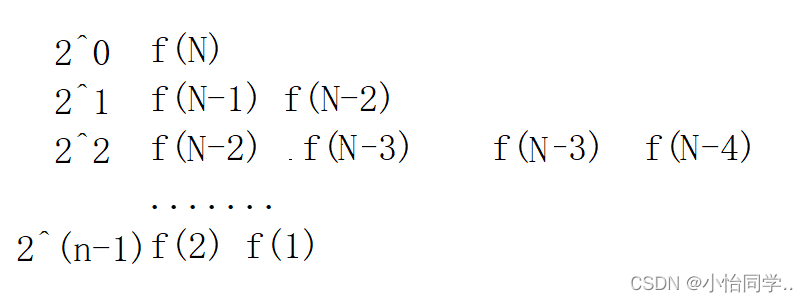
下列代码主要是递归思维 ,每次递归建立了一个栈帧
所以空间复杂度为(N)
long long Fac(size_t N)
{
if(N == 0)
return 1;
return Fac(N-1)*N;
}
每日一题
给定一个整数数组 nums,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
void swap(int left,int right,int*nums)
{int tmp =0;while(left < right){tmp = nums[left];nums[left] = nums[right];nums[right] = tmp;left++;right--;}}void rotate(int* nums, int numsSize, int k){
if(k > numsSize)
k = k%numsSize;//如果旋转数组大于numsSize swap(numsSize-k,numsSize-1,nums);//先逆序要旋转的
swap(0,numsSize-k-1,nums);//之后逆序不旋转的
swap(0,numsSize-1,nums);//最后整个数组在逆序一遍}