1.只有引用型操作，即只改变数组元素中的值，没有加工型操作，即不做插入删除操作

2.数组是多维结构，存储空间是一维结构

顺序映象方式：

1.行序为主序（低下标优先）

2.列序为主序（高下标优先）

eg：若三维数组[0,1][0,1,2][0,1]，以行序为主序，排列为（0,0,0）,（0,0,1）,（0,1,0）,（0,1,1）..

以列序为主序，排列为（0,0,0）,(1,0,0),(0,1,0),(1,1,0),(0,2,0),(1,2,0)...

假设每个元素占用L个存储单元，二维数组任意元素存储位置：LOC[i,j]=LOC[0,0]+(b2*i+j)*L;LOC[0,0]称基址或基地址

推广到n维：LOC[j1,j2,j3...]=LOC[0,0,0...]+L*该元素前的所有元素数，因此，数组元素的存储位置是线性函数，只要每个维度的长度确定，存储位置就确定，此时计算每个元素存储位置的时间相等，存储每个元素的时间是一样的，称其为顺序存储。

对于一个m行n列的数组，若其中存有t个非零元素，设t/（m*n）为稀疏因子，一般设稀疏因子小于0.05的矩阵为稀疏矩阵。稀疏矩阵存储时有大量的零，浪费存储空间，此外对稀疏矩阵做运算时对每个元素都需要判断与零的运算，大幅增大运算时间，因此需要对稀疏矩阵进行讨论，尽可能减少与零元素的计算，尽可能少存零元素，此外还要尽快找到所需要的元素。

矩阵转置的经典算法时间复杂度O（mu*nu），下面的算法会减少时间的使用

1.三元组法

#define MAXSIZE 12500
typedef struct {int i, j;//行数和列数int e;//元素值
}Triple;
typedef struct {int mu, nu, tu;//三元组行数、列数、非零元素个数Triple data[MAXSIZE + 1];//data[0]储存长度
}TSMatrix;

在Triple的基础上定义第二个结构体TSMatrix有利于某些矩阵运算如计算转置矩阵等，求转置矩阵的时间复杂度为O（mu*nu），代码双重循环即可实现。

表示方式：（（arr1，col1，num1），（arr2，col2，num2），（arr3，col3，num3）...）即可得到唯一的数组。

在双重循环求三元组的基础上可以加上两个辅助变量，首先按列求出相同列的元素数目记为Num为一个一维数组，再创建一个新数组cPot记录从第一列开始前n列非零元素之和。

下图为示例，左边为按行增序排列，右边为按列增序排列

 代码实现如下

int FastTransposeMatrix(TSMatrix T, TSMatrix* S) {S->mu = T.mu;S->nu = T.nu;S->tu = T.tu;int num[MAXSIZE], cpot[MAXSIZE], i ,col;for (i = 1; i <= T.nu; i++)num[i] = 0;for (i = 1; i <= T.tu; i++)num[T.data[i].j]++;cpot[1] = 1;for (i = 2; i <= T.nu; i++)cpot[i] = cpot[i - 1] + num[i + 1];//双重循环转置矩阵
}

若随机存取则从头查找，可以方便处理按顺序存储的矩阵

2.行逻辑连接的顺序表

给出结构定义

#define MAXMN 500
typedef struct {int mu, nu, tu;//三元组行数、列数、非零元素个数Triple data[MAXSIZE + 1];//data[0]储存元素个数int rpos[MAXMN + 1];
}RLSMatrix;

在快速算法中，虽然加快了速度，但是在M或N对应元素相乘时，若某一元素为零，结果显然为零，快速算法没有考虑到这种情况，因此用rpos存储有关信息进而加速。

实际操作时，使用累加器ctemp，假设M矩阵有i行j列，i从1到n，对每一行都先检测是否有N矩阵的列与其相乘结果不为零，即M（i，j）与N（j，k）相乘，并对于不同的k将接过放在不同的累加器中。对每一行都可以将乘出的Q（i，k）存储进Q.data中。Q.data视做一个一维数组，rpos记录每行第一个非零元素在Q.data中的位置。

代码实现如下

int MultSMatrix(RLSMatrix M, RLSMatrix N, RLSMatrix* Q) {int arow, brow, tp, p, q, tq, ccol;int ctmp[];//累加器if (M.nu != N.mu) {printf("ERROR");return 0;}Q->mu = M.mu, Q->nu = N.nu, Q->tu = 0;if (M.mu * N.nu != 0) {for (arow = 1; arow = M.mu + 1; arow++) {ctmp[arow] = 0;if (arow < M.mu)tp = M.rpos[arow + 1];elsetp = M.tu + 1;for (p = M.rpos[arow]; p < M.rpos[arow] + 1; p++) {if (brow < N.mu)tq = N.rpos[arow + 1];elsetq = N.tu + 1;for (q = N.rpos[arow] + 1; q < tq; q++) {ccol = N.data[q].j;ctmp[ccol] += M.data[p].i * N.data[q].j;}}}for (ccol = 1; ccol <= Q->nu; ccol++) {if (ctmp[ccol]){Q->data[Q->tu] = (arow, ccol, ctmp[ccol]);if (Q->tu++ > MAXSIZE) {printf("ERROR");return 0;}}}}return 1;
}

该方法的时间复杂度为O（M.mu*N.nu）。

3.十字链表

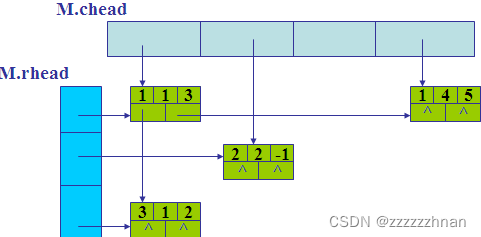
若矩阵中非零元个数变化较大时，宜使用十字链表。例如两个矩阵相加，此时可能非零元素变为零元素，或零元素变为非零元素，若使用上面两种算法，元素的位置变化会比较多且繁杂。

十字链表总体需要五个变量：非零元素，该元素所在的行列数和系数矩阵的行列数。每存储一个非零元素，有right和down指针指向同一行和同一列的下一个非零元素；为便于寻找数据，用一维数组mhead和rhead存储每一行、列的头指针。由此得出结构体定义

typedef struct _ONode {int i, j;//非零元素所在的行号列号int e;//非零元素的值struct _ONode* right, * down;//指向右和向下的指针
}ONode, * OLink;typedef struct {OLink* mhead, * rhead;int mu, nu, tu;//稀疏矩阵的行数、列数、非零元素个数
}CrossList;

*对pq定义类型存疑

建立十字链表

int CreateMatrixLink(CrossList* M) {if (M)free(M);int m, n, t;scanf("%d %d %d", &m, &n, &t);M->mu = m, M->nu = n, M->tu = t;//初始化结点if (!(M->mhead = (OLink*)malloc(sizeof(OLink) * (m + 1))))exit(OVERFLOW);if (!(M->chead = (OLink*)malloc(sizeof(OLink) * (n + 1))))exit(OVERFLOW);M->mhead = M->chead = NULL;int i, j, e;for (scanf(&i, &j, &e);i!=0; scanf(&i, &j, &e)) {if(!(p=(ONode*)malloc(sizeof(ONode))))exit(OVERFLOW);p.i = i, p.j = j, p.e = e;//p从行头插入，第i行无元素或M.head[i]结点在p右边的情况if (M->mhead[i] == NULL || M->mhead[i]->j > j) {p.right = M->mhead[i];M->mhead[i] = p;}//M.head[i]在p左边（一般情况）else {//对第i列进行行插入for (q = M.mhead[i]; (q.right.j < j) && (q.right); q = q.right) {p.right = q.right;q.right = p;}}//对列做相同操作if (M->chead[j] == NULL || M->chead[j]->i > i) {p.down = M->chead[j];M->chead[j] = p;}else {for (q = M.chead[j]; (q.down.i < i) && (q.down); q = q.down) {p.down = q.down;q.down = p;}}}return 1;
}

 对稀疏矩阵相加有四种情况：

1.a矩阵元素为零，则结点值为b矩阵元素值

2.b矩阵元素为零，则结点值不变

3.元素值变为ab矩阵元素值相加

4.值变为0，删除该结点地址

实现时，设指针pa，pb指向某行，pa==NULL表示该行没有非零元

pa->j < pb->j
//向右移动pa即可，递推(pa->j == pb->j) && (pa->e + pb->e == 0)
//删除pa指向的结点地址，同时要注意改变pa前一个的right值和上一个的down值（指向另外的结点地址）(pa->j == pb->j) && (pa->e + pb->e != 0)
//改变pa指向的结点值即可pa->j > pb->j || pa == NULL;
//在pa前增加一个结点地址，改变同一行中前一个结点的right和同一列中上一个节点的down

代码实现较容易，不过多叙述

广义表

广义表一般记为LS=（a1，a2...an），广义表中的数据如果是单个元素称为原子，如果是广义表则称为子表。原子的深度为0，子表的深度为1。n为广义表的长度，深度为广义表括号的重数，原子的深度为0，空表的深度为1。

广义表如果非空，称第一个数据为表头，其余的数据为表尾。若表中无元素，长度为0，为空表，表示为LS=（）；若只有一个子表且为一个空表，则表头和表尾均为空，长度为1，表示为LS=（（））。广义表的子表也可以是它本身，因此他是一个递归结构，可以看做递归版的链表。

由于表中元素有不同的类型，因此定义广义表的结构体时要用到枚举和联合，同时需要一个标记域。对表结点，存在标记域和前后两个指针，对原子结点，存在标记域和向后指的指针。

定义结构体有两种不同的方法

//递归构建广义表
typedef enum { ATOM, LIST }tag;
typedef struct GLNode{int tag;union {AtomType atom;struct { struct GLNode* hp, * tp; }ptr;};
}*GList;//由于表结点和原子结点都需要向后指的指针，所以可以将原子结点的元素与表结点的前指针联合声明
typedef enum { ATOM, LIST }tag;
typedef struct GLNode {int tag;union {AtomType atom;struct GLNode* hp;};struct GLNode* tp;
}*GList;

广义表主要的操作为递归实现求广义表的深度，新建一个广义表，复制一个广义表。

//求广义表的深度
int DepthGLists(GList& GL) {if (!GL)max = 1;if (GL->tag == ATOM)max = 0;for(max=0,p=GL;p;p=GL->ptr.tp){if (DepthGLists(p.ptr.hp) > max)max = DepthGLists(p.ptr.hp);return max;
}

//复制广义表
//第一种定义方式int CopyGLists(GList & GL, GList L) {if (!GL)return ERROR;else {if(!(L = (GList)malloc(sizeof(GNode))))exit(OVERFLOW);L.tag = GL.tag;//在第一种定义方式下，原子结点只有一个域if (GL.tag == ATOM)L.atom = GL.atom;else {CopyGLists(GL.ptr.hp, L.ptr, hp);CopyGLists(GL.ptr.tp, L.ptr, tp);}}return OK;
}

//由一个字符串建立广义表int CreateGLists(GList& GL,SString S) {if (!GL)return NULL;else {if (!(p = (GList)malloc(sizeof(GLNode)));exit(OVERFLOW);else {sever(sub, hsub);//对表头建立广义表if (Strlength(hsub) == 1) {p.ptr.hp->tag = ATOM;p.ptr.hp->atom = hsub;}else {CreateGLists(p.ptr.hp, hsub);}//对表尾建广义表if (!StrEmpty(sub)) {CreateGLists(p.ptr.tp, sub);}elsep.ptr.tp = NULL;}}
}