声明：本文仅为个人学习记录所用，参考较多，如有侵权，联系删除

决策树

通俗来说，决策树分类的思想类似于找对象。现想象一个女孩的母亲要给这个女孩介绍男朋友，于是有了下面的对话：

  女儿：多大年纪了？母亲：26。女儿：长的帅不帅？母亲：挺帅的。女儿：收入高不？母亲：不算很高，中等情况。女儿：是公务员不？母亲：是，在税务局上班呢。女儿：那好，我去见见。这个女孩的决策过程就是典型的分类树决策。相当于通过年龄、长相、收入和是否公务员对将男人分为两个类别：见和不见。假设这个女孩对男人的要求是：30岁以下、长相中等以上并且是高收入者或中等以上收入的公务员，下图表示了女孩的决策逻辑。

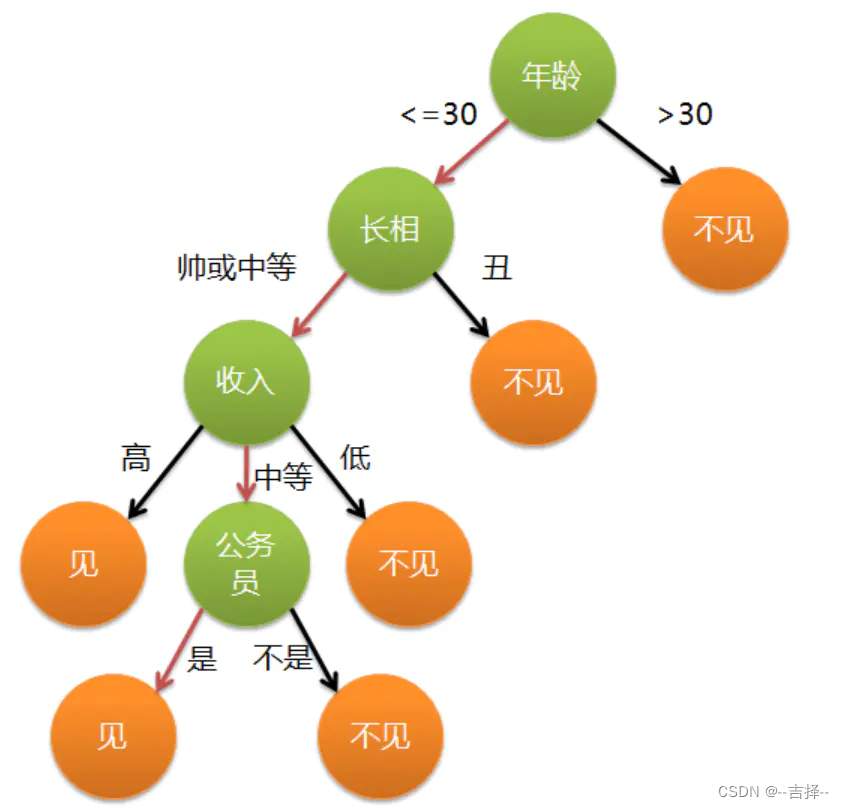
在这里插入图片描述
如果你作为一个女生，你会优先考虑哪个条件：长相？收入？还是年龄。在考虑年龄条件时使用25岁为划分点，还是35岁为划分点。有这么多条件，用哪个条件特征先做if，哪个条件特征后做if比较优呢？还有怎么确定用特征中的哪个数值作为划分的标准。这就是决策树机器学习算法的关键了。

集成学习

假设我们现在提出了一个复杂的问题，并抛给几千个随机的人，然后汇总他们的回答。在很多情况下，我们可以看到这种汇总后的答案会比一个专家的答案要更好。这个称为“群众的智慧”。同理，如果我们汇总一组的预测器（例如分类器与回归器）的预测结果，我们可以经常获取到比最优的单个预测器要更好的预测结果。这一组预测器称为一个集成，所以这种技术称为集成学习，一个集成学习算法称为一个集成方法。

随机森林

假如训练一组决策树分类器，每个都在训练集的一组不同的随机子集上进行训练。在做决策时，我们可以获取所有单个决策树的预测结果，然后根据各个结果对每个类别的投票数，最多票的类别获胜。这种集成决策树称为随机森林。尽管它非常简单，不过它是当前最强大的机器学习算法之一。

一个树和1000个树

假如有一个弱学习者（weak learner，也就是说它的预测能力仅比随机猜稍微高一点），分类正确的概率是51%。本来不应该考虑这种弱分类器（分类能力强的还有很多种方法），但是，假如我们考虑把1000个这样的树放在一起（一个集合），预测结果如何呢？
·每个决策树都使用所有数据作为训练集
·节点的选择是通过在所有特征中进行搜索选出最好的划分方式得到的
·每个决策树的最大深度都是1

import pandas as pd
import numpy as np# 导入鸢尾花数据集
from sklearn.datasets import load_iris# 从样本中随机按比例选取训练集和测试集
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import BaggingClassifier
# To measure performance
from sklearn import metrics
# 该数据集一共包含4个特征变量，1个类别变量。共有150个样本。
iris = load_iris()
X = pd.DataFrame(iris.data[:, :], columns = iris.feature_names[:])
# print(X)
y = pd.DataFrame(iris.target, columns =["Species"])# 划分数据集
# 随机数种子：其实就是该组随机数的编号，在需要重复试验的时候，保证得到一组一样的随机数。
# 随便填一个大于0的数据就能保证，其他参数一样的情况下得到的随机数组是一样的。但填0或不填，每次都会不一样。
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 20, random_state = 100)# 定义决策树
stump = DecisionTreeClassifier(max_depth = 1)# bagging集成方法
ensemble = BaggingClassifier(estimator = stump, n_estimators = 1000,bootstrap = False)# 训练分类器
stump.fit(X_train, np.ravel(y_train))
ensemble.fit(X_train, np.ravel(y_train))# 预测
y_pred_stump = stump.predict(X_test)
y_pred_ensemble = ensemble.predict(X_test)# 决策表现
stump_accuracy = metrics.accuracy_score(y_test, y_pred_stump)
ensemble_accuracy = metrics.accuracy_score(y_test, y_pred_ensemble)print(f"The accuracy of the stump is {stump_accuracy*100:.1f} %")
print(f"The accuracy of the ensemble is {ensemble_accuracy*100:.1f} %")

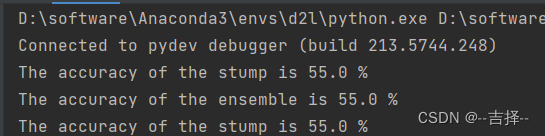
在这里插入图片描述
可以看到无论是一棵树还是1000棵树，预测准确率都一样。

随机森林-RandomForest

上面1000棵树虽然构成了一片森林，但是每棵树都一样，相当于你问一只兔子爱吃青菜还是爱吃肉，问1000遍，结果都是一样的，这不叫群众的智慧！
如果我们：
·每个决策树都使用随机采样得到的子集作为训练集，采样方式为bootstrap(一种有放回抽样)
·节点的选择是通过在子集中随机选择特征（不是所有特征）中进行搜索选出最好的划分方式得到的
·每个决策树的最大深度都是1

# max_features：寻找最佳切分时考虑的最大特征数，默认是所有特征都用
# splitter：用于在每个节点上选择拆分的策略。可选“best”, “random”，默认“best”。
stump = DecisionTreeClassifier(max_depth = 1, splitter = "best", max_features = "sqrt")# 随机森林
# n_estimators基分类器的个数
ensemble = BaggingClassifier(estimator = stump, n_estimators = 1000,bootstrap = True)
stump.fit(X_train, np.ravel(y_train))
ensemble.fit(X_train, np.ravel(y_train))y_pred_tree = stump.predict(X_test)
y_pred_ensemble = ensemble.predict(X_test)stump_accuracy = metrics.accuracy_score(y_test, y_pred_stump)
ensemble_accuracy = metrics.accuracy_score(y_test, y_pred_ensemble)print(f"The accuracy of the stump is {stump_accuracy*100:.1f} %")
print(f"The accuracy of the Random Forest is {ensemble_accuracy*100:.1f} %")

![在这里插入图片描述](https://img-blog.csdnimg.cn/9bb47d0e22304e53ab852cbacdeecc3d.png
群众的智慧这不就体现出来了吗！
在不同的训练集随机子集上进行训练（也就是将训练集上的数据随机抽样为若干个子集，然后用这些不同子集在同一种模型上训练，这样就形成了不一样的预测器）

极度随机树-Extremely randomized trees，Extra tree

在选定了划分特征后，RF的决策树会基于信息增益，基尼系数，均方差之类的原则，选择一个最优的特征值划分点，这和传统的决策树相同。但是Extra tree比较的激进，会随机的选择一个特征值来划分决策树。
由于随机选择了特征值的划分点位，而不是最优点位，这样会导致生成的决策树的规模一般会大于RF所生成的决策树。也就是说，模型的方差相对于RF进一步减少，但是bias相对于RF进一步增大。在某些时候，Extra tree的泛化能力比RF更好.
在这里插入图片描述

stump = DecisionTreeClassifier(max_depth=1, splitter="random", max_features="sqrt")
ensemble = BaggingClassifier(estimator=stump, n_estimators=1000, bootstrap=False)stump.fit(X_train, np.ravel(y_train))
ensemble.fit(X_train, np.ravel(y_train))y_pred_tree = stump.predict(X_test)
y_pred_ensemble = ensemble.predict(X_test)stump_accuracy = metrics.accuracy_score(y_test, y_pred_stump)
ensemble_accuracy = metrics.accuracy_score(y_test, y_pred_ensemble)print(f"The accuracy of the stump is {stump_accuracy * 100:.1f} %")
print(f"The accuracy of the Extra Trees is {ensemble_accuracy * 100:.1f} %")

在这里插入图片描述

补充 hard voting soft voting

在这里插入图片描述

补充 Bootstrap

Bootstrap又称自展法、自举法、自助法、靴带法 , 是统计学习中一种重采样(Resampling)技术，用来估计标准误差、置信区间和偏差
子样本之于样本，可以类比样本之于总体
举例
栗子：我要统计鱼塘里面的鱼的条数，怎么统计呢？
假设鱼塘总共有鱼N，不知道N是多少条
步骤：
承包鱼塘，不让别人捞鱼(规定总体分布不变)。
自己捞鱼，捞100条，都打上标签(构造样本)
把鱼放回鱼塘，休息一晚(使之混入整个鱼群，确保之后抽样随机)
开始捞鱼，每次捞100条，数一下，自己昨天标记的鱼有多少条，占比多少(一次重采样取分布)。
然后把这100条又放回去
重复3，4步骤n次。建立分布。
（原理是中心极限定理）

假设一下，第一次重新捕鱼100条，发现里面有标记的鱼12条，记下为12%，
放回去，再捕鱼100条，发现标记的为9条，记下9%，
重复重复好多次之后，假设取置信区间95%，
你会发现，每次捕鱼平均在10条左右有标记，

它怎么来的呢？
10/N=10%

所以，我们可以大致推测出鱼塘有1000条左右。

其实是一个很简单的类似于一个比例问题。这也是因为提出者Efron给统计学顶级期刊投稿的时候被拒绝的理由–“太简单”。这也就解释了，为什么在小样本的时候，bootstrap效果较好，

你这样想，如果我想统计大海里有多少鱼，你标记100000条也没用啊，因为实际数量太过庞大，
你取的样本相比于太过渺小，最实际的就是，你下次再捕100000的时候，发现一条都没有标记，就尴尬了。。。

参考文献

[1] 决策树（Decision Tree）
[2] 集成学习与随机森林（一）投票分类器
[3] Hard Voting 与 Soft Voting 的对比
[4] 统计学中的Bootstrap方法（Bootstrap抽样）用来训练bagging算法，如果随机森林Random Forests
[5] An Intuitive Explanation of Random Forest and Extra Trees Classifiers