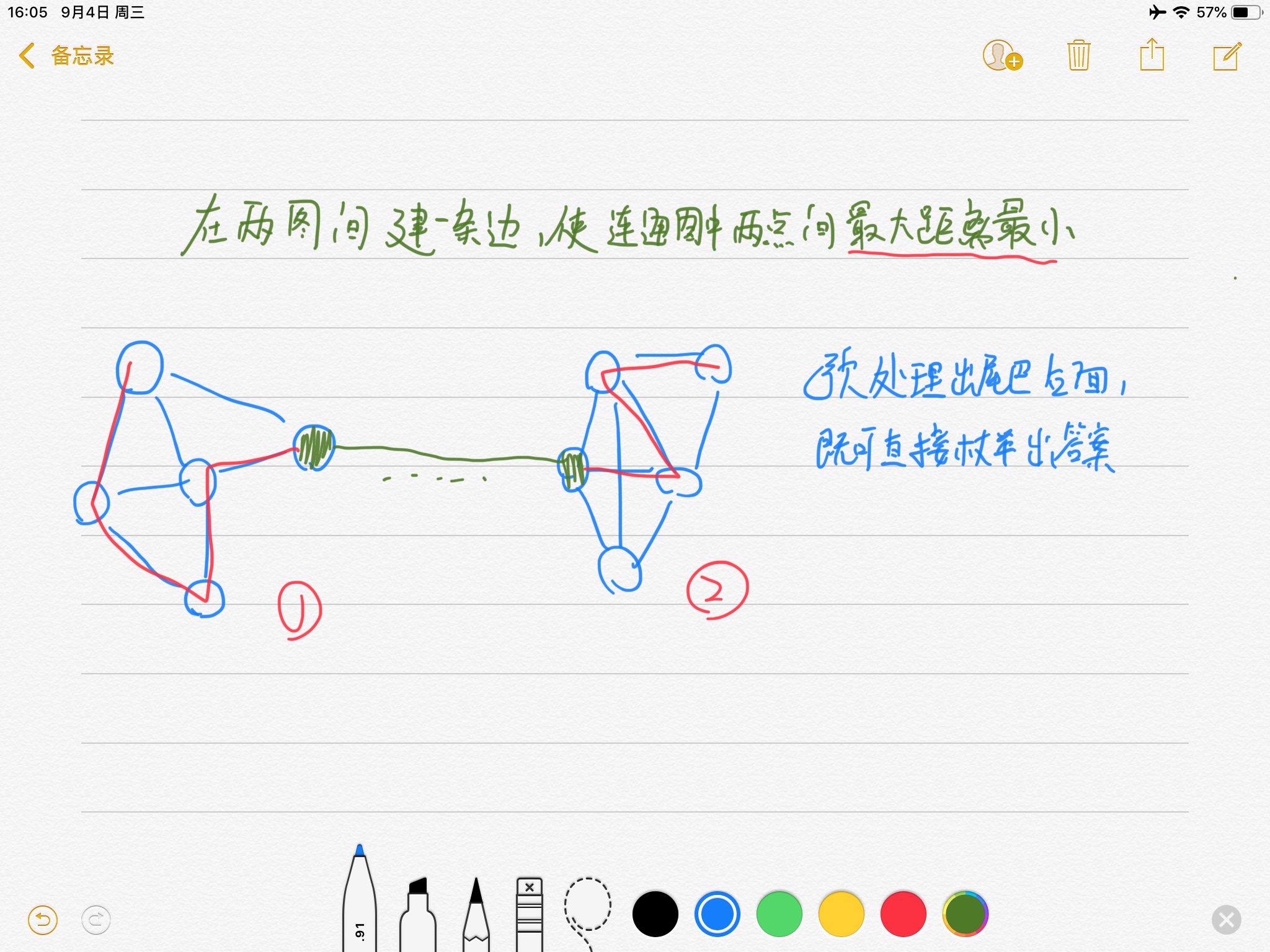
题意：

题目链接：https://www.51nod.com/onlineJudge/questionCode.html#!problemId=1522

---

思路：

很好的区间dp。
从1开始填起，两个1能存在的位置分别是1和2，1和2*n，2*n-1和2*n。根据每种不同的填法，就可以得到不同区间，这时候问题就变成了在下一个区间从2开始填起。
可以发现对于一个区间[l,r]，当前要填x，我们有三种填当前数的方案，根据这三种方案，就可以递归得到更小区间的子问题。最后最小的问题一定是两个相邻的位置，填上最大的数n。
这样就可以想到区间dp，dp[i][j]是区间[i,j]的方案数，那么状态转移方程是：
dp[i][j] = dp[i + 2][j] + dp[i][j - 2] + dp[i + 1][j - 1];
但是题目还有要求满足的条件，很显然，按照这样的填法，后得到子问题的区间里的数一定比之前填的要大，所以每次状态转移的时候，都要判断k个条件是否满足，check(l,r,p,q)表示[l,r]内的数要大于外面的数，且位置p的数要等于位置q的数。
dp很好写，判断条件比较烦。

---

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int MAXN = 105;struct node {int cmp, x, y;
} a[MAXN];int n, k;
char s[3][3];int getCmp(char s[]) {if (strcmp(s, "=") == 0) return 1;if (strcmp(s, ">") == 0) return 2;if (strcmp(s, "<") == 0) return 3;if (strcmp(s, ">=") == 0) return 4;return 5;
}bool check(int l, int r, int p, int q) {for (int i = 1; i <= k; i++) {int cmp = a[i].cmp, x = a[i].x, y = a[i].y;bool tx = (x >= l && x <= r), ty = (y >= l && y <= r);bool px = (x == p || x == q), py = (y == p || y == q);if (cmp == 1 && ((tx != ty) || (px != py))) return false;if (cmp == 2 && ((!tx && (ty || py)))) return false;if (cmp == 3 && ((!ty && (tx || px)))) return false;if (cmp == 4 && (((!tx && !px) && (ty || py)) || (px && ty))) return false;if (cmp == 5 && (((!ty && !py) && (tx || px)) || (py && tx))) return false;}return true;
}LL dp[MAXN][MAXN];int main() {//freopen("in.txt", "r", stdin);scanf("%d%d", &n, &k);bool flag = true;int cnt = 0;for (int i = 1; i <= k; i++) {for (int j = 0; j < 3; j++)scanf("%s", s[j]);int x = atoi(s[0]), y = atoi(s[2]);//cout << x << " " << y << endl;int cmp = getCmp(s[1]);if (x == y) {if (cmp == 2 || cmp == 3) flag = false;continue;}a[++cnt] = (node) {cmp, x, y};}if (!flag) {puts("0");return 0;}k = cnt;for (int i = 1; i < 2 * n; i++) {bool tag = true;for (int j = 1; j <= k; j++) {int cmp = a[j].cmp, x = a[j].x, y = a[j].y;if ((x == i && y == i + 1) || (x == i + 1 && y == i)) {if (cmp == 2 || cmp == 3) {tag = false; break;}}}if (tag) dp[i][i + 1] = 1;}for (int l = 4; l <= 2 * n; l += 2) {for (int i = 1; i <= 2 * n - l + 1; i++) {int j = i + l - 1;if (check(i + 2, j, i, i + 1)) dp[i][j] += dp[i + 2][j];if (check(i, j - 2, j - 1, j)) dp[i][j] += dp[i][j - 2];if (check(i + 1, j - 1, i, j)) dp[i][j] += dp[i + 1][j - 1];}}printf("%I64d\n", dp[1][2 * n]);return 0;
}