本文就红黑树的插入操作进行细致到每一个小步骤的解析。
1,成员变量
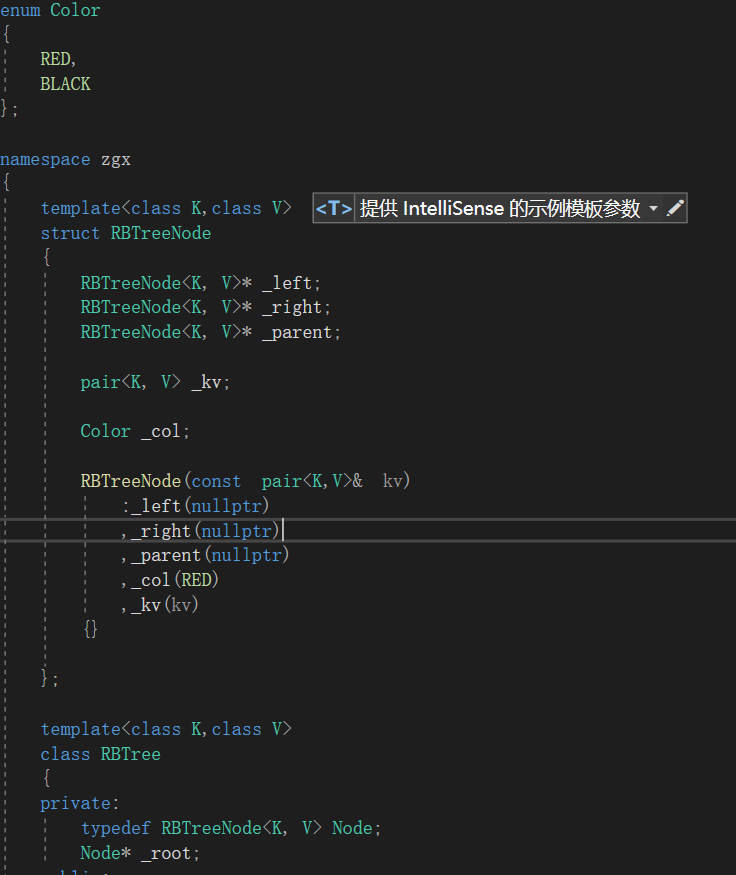
本红黑树使用了三叉链结构,使用的时候尤其要记得处理指向父亲的指针。
为何在节点的构造函数中,默认节点的颜色为红色?
因为考虑到红黑树的性质(对于每个结点,从该结点到其所有后代叶结点的简单路径上,均 包含相同数目的黑色结点),所以设置为红色是最为合理方便的,如果插入的时候会有连续的红色节点,再做调整也很方便。
但是如果默认为黑节点,就要做调整保证每个路径上的黑节点相同,相比之下会很麻烦。
2,Insert函数的实现(分为各个细节讨论)
2,1插入时,红黑树是否为空树

考虑到此情况,要先判断红黑树是否为空树。
若是,进行相关操作后return
若不是,向下进行
2,2若不是空树,迭代到树的底部,并插入节点
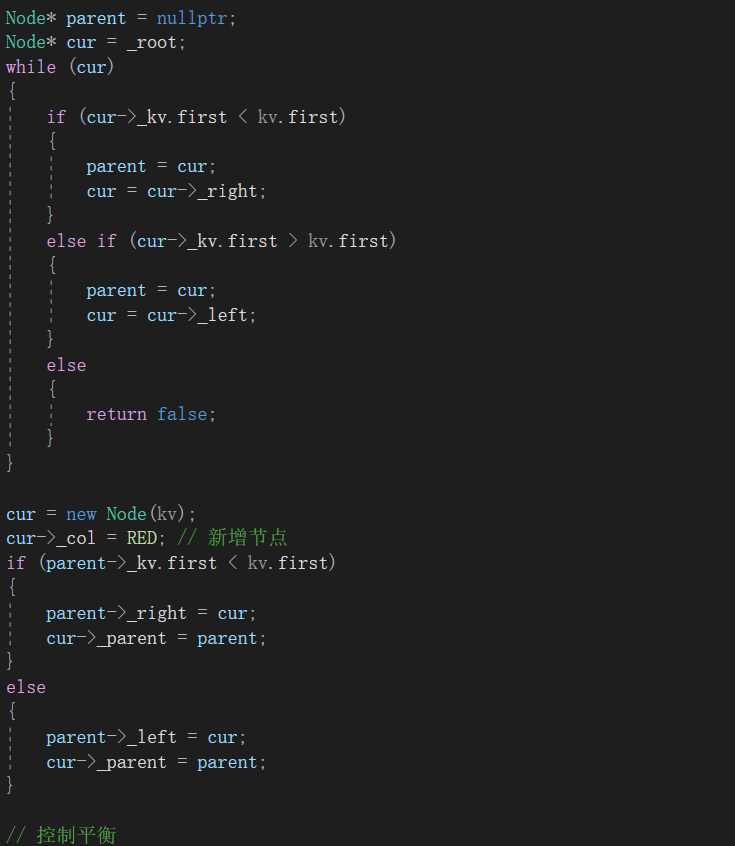
不必担心parent的空指针解引用问题,由于不是空树,所以parent一定不会为nullptr。
2,3插入节点后,控制平衡
理论基础:
理论:(我们先约定:cur为当前节点,p为父节点,g为祖父节点,u为叔叔节点)
情况一: cur为红,p为红,g为黑,u存在且为红
如下图:
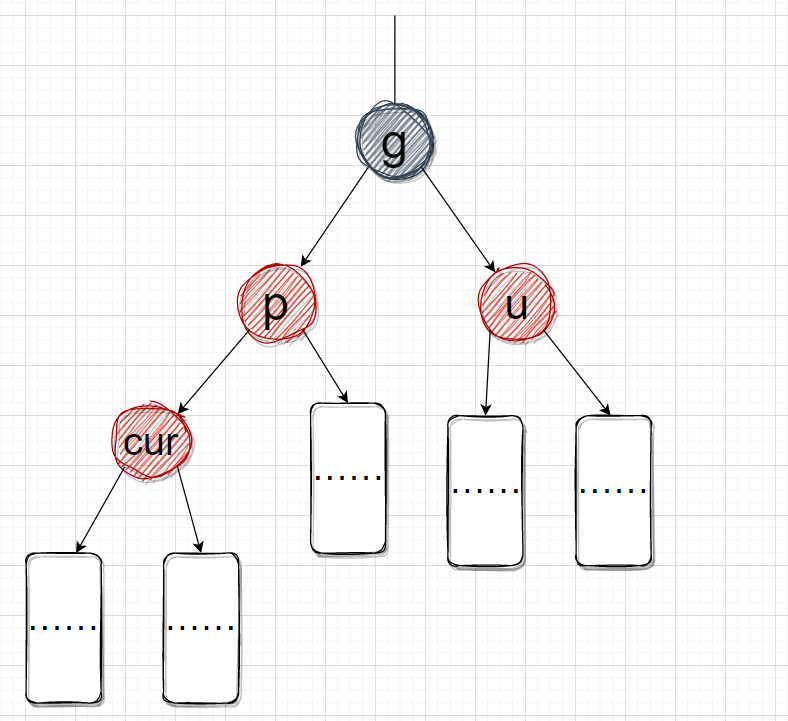
此图是个抽象图,代表着多种情况,带省略号的长方形表示一个未知的树。
解决方法:
将p,u改为黑,g改为红,然后把g当成cur,继续向上调整
如果g是根节点,调整完成后,需要将g改为黑色(其实只要在调整操作的最后将_root的颜色置为黑色就行,不必在每种情况下特殊处理)
如果g是子树,g一定有双亲,且g的双亲如果是红色,需要继续向上调整。
——————————————————————————————————————
情况二: cur为红,p为红,g为黑,u不存在/u存在且为黑,且为单旋情况
如下图:
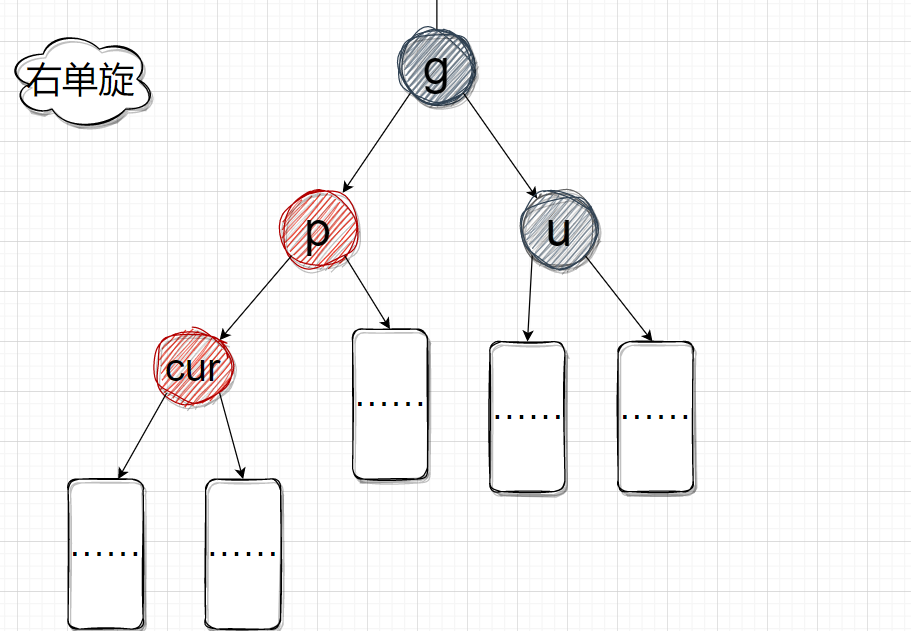
如下图:

解决方法:
p为g的左孩子,cur为p的左孩子,则进行右单旋转;相反,
p为g的右孩子,cur为p的右孩子,则进行左单旋转
p、g变色--p变黑,g变红
旋转函数:
1,左单旋
解释:
要实现一个操作,往往有多种方法,函数的设计也有多种。
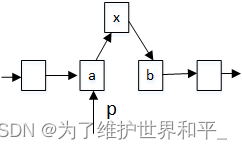
本人选择将旋转函数参数统一设置为要处理的两个节点中处于上方的节点。
如图:
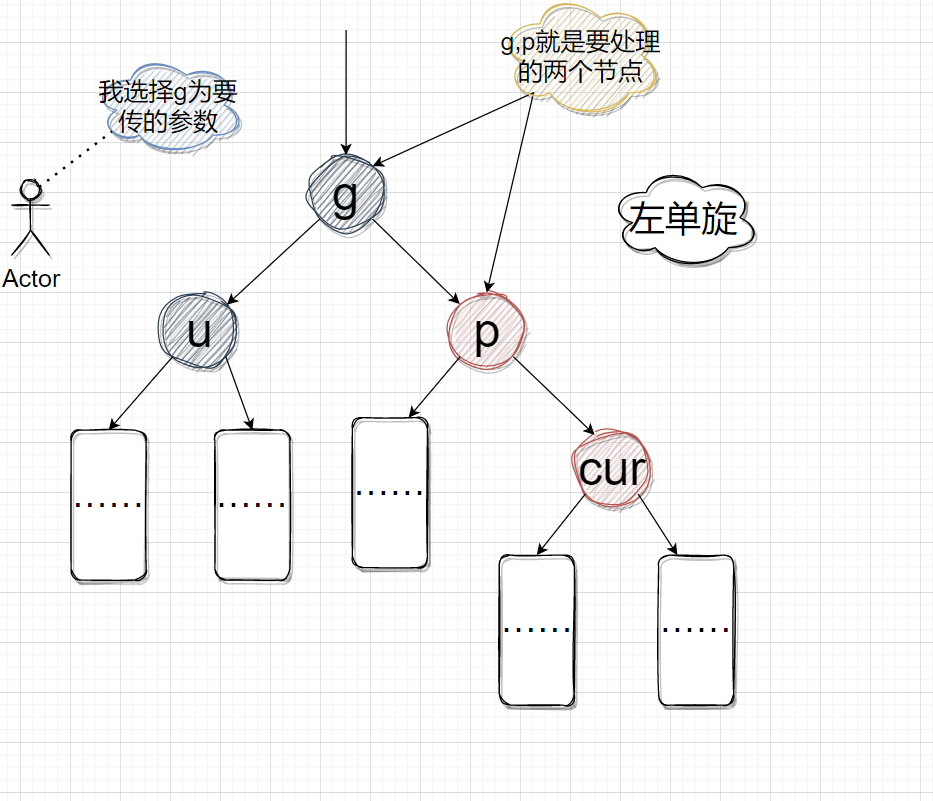
于是,写出代码实现如下:
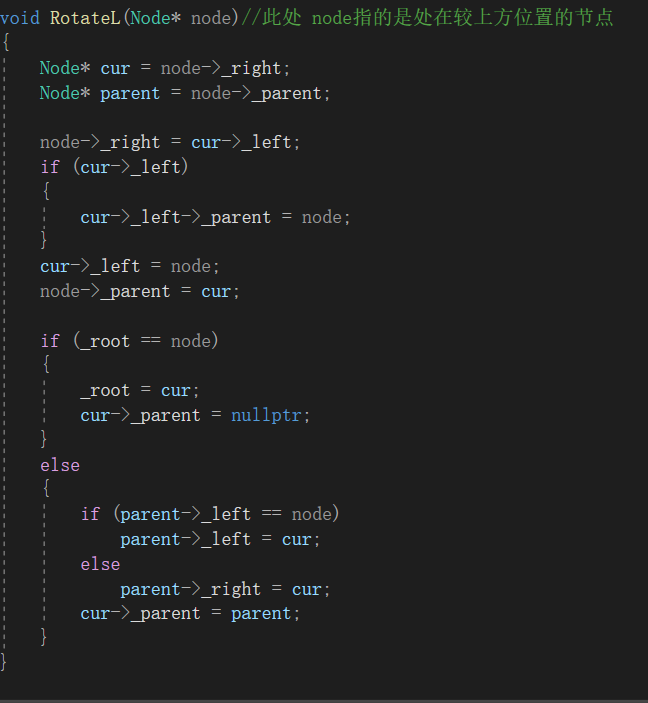
cur是node的右子节点,parent是node的父节点。
要特别注意,此时使用的是三叉链结构,在链接节点的同时,一定不要忘记对_parent进行处理
在对_parent进行处理时,当然也要注意_parenrt是否存在,所以我们还要判断node是否为根节点,再进行相关操作。
2,右单旋
分析同上,不在赘述。
如下图:

代码实现:

————————————————————————————————————————
在插播了左单旋和右单旋的实现后,继续回来讨论第三种情况
情况三:cur为红,p为红,g为黑,u不存在/u存在且为黑,且需要双旋
有了以上基础,此处直接上图。


解决方法:
p为g的左孩子,cur为p的右孩子,则针对p做左单旋转,再对g做右单旋转;相反,
p为g的右孩子,cur为p的左孩子,则针对p做右单旋转,再对g做左单旋转。
将cur置为黑色,g置为红色
代码实现:
复用左单旋和右单旋即可。

代码实现:
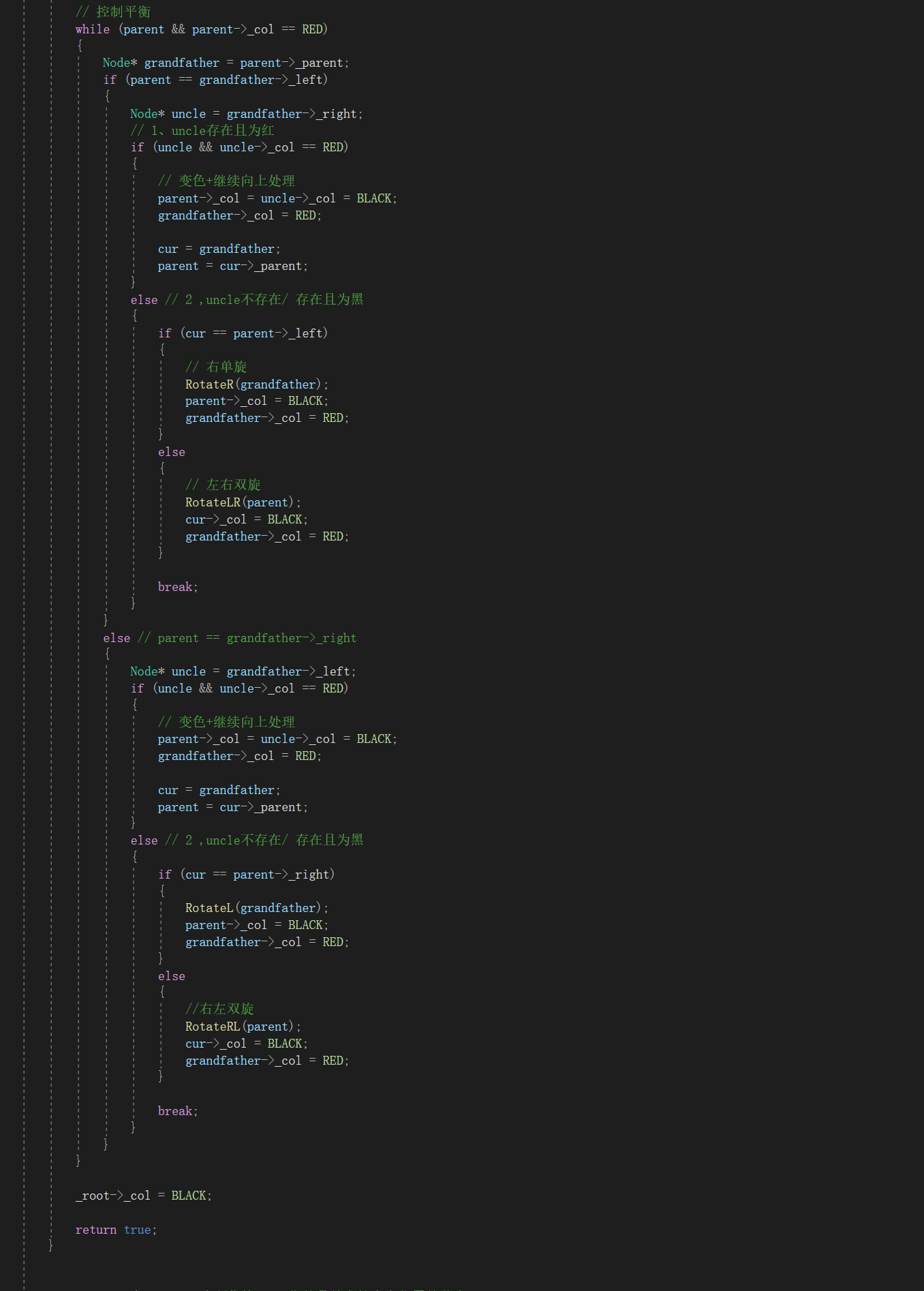
解释:
整个循环结束的条件是parent不存在或者parent为黑色
并且不必担心祖父是否存在,因为如果parent && parent->_col == RED的话,
祖父节点一定存在,并且为黑色,因为parent为红色节点,不可能是根节点。
如果是第一种情况的话,是需要迭代调整的:要将g的位置变为cur,继续向上检查。
而第二三种情况则不需要,因为旋转了之后,没有对上层产生影响,所以可以在调整之后直接跳出
循环结束后,将_root置为黑色,保证结构即可。