剑指 Offer 47. 礼物的最大价值

难度：$middle$

---

题目描述

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:

输入: 
[[1,3,1],[1,5,1],[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

提示：

• $0<grid.length<=200$
• $0<grid[0].length<=200$

---

算法

(动态规划)

从棋盘的左上角开始拿格子里的礼物，并每次 向右 或者 向下 移动一格、直到到达棋盘的右下角。

根据题目说明，易得某单元格只可能从上边单元格或左边单元格到达。

设 f(i,j) 为从棋盘左上角走至单元格 (i,j) 的礼物最大累计价值，易得到以下递推关系：f(i,j) 等于 f(i,j−1) 和 f(i−1,j) 中的较大值加上当前单元格礼物价值 grid(i,j) 。

• f(i,j)=max[f(i,j−1),f(i−1,j)]+grid(i,j)

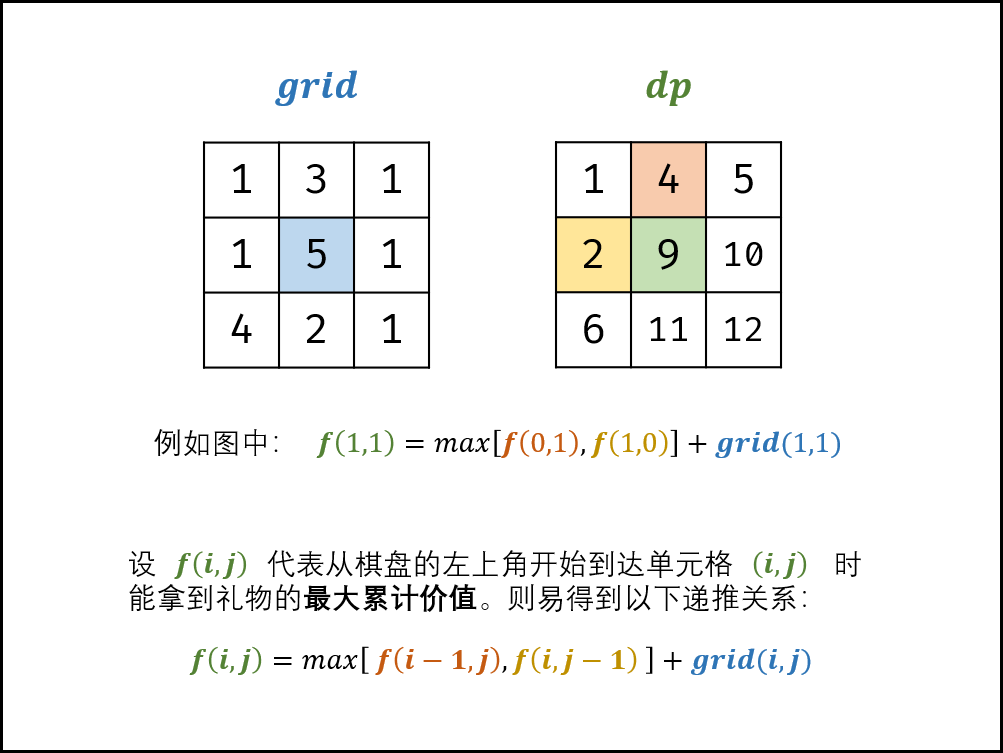
• 状态定义： 设动态规划矩阵 dp(i,j) 代表从棋盘的左上角开始，到达单元格 (i,j) 时能拿到礼物的最大累计价值。
• 转移方程：
  • 当 i=0 且 j=0 时，为起始元素；
  • 当 i=0 且 j≠0 时，为矩阵第一行元素，只可从左边到达；
  • 当 i≠0 且 j=0 时，为矩阵第一列元素，只可从上边到达；
  • 当 i≠0 且 j≠0 时，可从左边或上边到达；

初始状态： dp[0][0]=grid[0][0] ，即到达单元格 (0,0) 时能拿到礼物的最大累计价值为 grid[0][0] ；
返回值： dp[m−1][n−1] ，m , n 分别为矩阵的行高和列宽，即返回 dp 矩阵右下角元素。

复杂度分析

• 时间复杂度：$O(n)$，其中 $n$ 是链表的长度。需要遍历链表一次

• 空间复杂度 : $O(1)$

C++ 代码

多开辟一维的空间，可以避免判断一些边界情况，f[1][1] = grid[0][0]

class Solution {
public:int maxValue(vector<vector<int>>& grid) {int n = grid.size(), m = grid[0].size();vector<vector<int>> f(n + 1, vector<int>(m + 1));for (int i = 1; i <= n; i ++) {for (int j = 1; j <= m; j ++) {f[i][j] = max(f[i - 1][j], f[i][j - 1]) + grid[i - 1][j - 1];}}return f[n][m];}
};

---