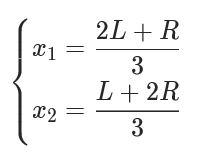1512、给你一个整数数组 nums 。

如果一组数字 (i,j) 满足 nums[i] == nums[j] 且 i < j ，就可以认为这是一组 好数对 。

返回好数对的数目。

示例 1：

输入：nums = [1,2,3,1,1,3]
输出：4
解释：有 4 组好数对，分别是 (0,3), (0,4), (3,4), (2,5) ，下标从 0 开始

 map映射每个key对应的个数，用n(n-1)/2得出每个key可能的排列数。

class Solution {
public:int numIdenticalPairs(vector<int>& nums) {map<int, int> mp;for(int i= 0; i < nums.size(); i++)mp[nums[i]]++;int ans = 0;for(auto it = mp.begin(); it != mp.end(); it++)ans += (it->second * (it->second - 1) / 2);return ans;}
};

 结果：

执行用时：4 ms, 在所有 C++ 提交中击败了53.10% 的用户

内存消耗：7.7 MB, 在所有 C++ 提交中击败了100.00% 的用户

 

修改：减少一次循环。遇到一个数key，与在其之前的每一个数mp[key]均构成组合，ans += mp[key]++；

class Solution {
public:int numIdenticalPairs(vector<int>& nums) {map<int, int> mp;int ans = 0;for(int i= 0; i < nums.size(); i++)ans += mp[nums[i]]++;return ans;}
};

结果：

执行用时：0 ms, 在所有 C++ 提交中击败了100.00% 的用户

内存消耗：7.6 MB, 在所有 C++ 提交中击败了100.00% 的用户

 

1513、给你一个二进制字符串 s（仅由 '0' 和 '1' 组成的字符串）。

返回所有字符都为 1 的子字符串的数目。

由于答案可能很大，请你将它对 10^9 + 7 取模后返回。

示例 1：

输入：s = "0110111"
输出：9
解释：共有 9 个子字符串仅由 '1' 组成
"1" -> 5 次
"11" -> 3 次
"111" -> 1 次

 遍历找仅含1的子序，其长度为n，则组合数为n(n+1)/2。注意mod，直接将数据类型设成long long比较稳妥，不然会报错。

class Solution {
public:int MOD = 1e9 + 7;int numSub(string s) {long long cnt = 0, ans = 0;for(int i = 0; i < s.size(); i++) {if(s[i] == '0' && cnt > 0){ans += ((cnt + 1) * cnt / 2) % MOD;cnt = 0;}if(s[i] == '1') cnt++;}ans += ((cnt + 1) * cnt / 2) % MOD;return ans;}
};

结果：

执行用时：36 ms, 在所有 C++ 提交中击败了76.23% 的用户

内存消耗：8.8 MB, 在所有 C++ 提交中击败了100.00% 的用户

 

1514、给你一个由 n 个节点（下标从 0 开始）组成的无向加权图，该图由一个描述边的列表组成，其中 edges[i] = [a, b] 表示连接节点 a 和 b 的一条无向边，且该边遍历成功的概率为 succProb[i] 。

指定两个节点分别作为起点 start 和终点 end ，请你找出从起点到终点成功概率最大的路径，并返回其成功概率。

如果不存在从 start 到 end 的路径，请 返回 0 。只要答案与标准答案的误差不超过 1e-5 ，就会被视作正确答案。

示例1：

输入：n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
输出：0.25000
解释：从起点到终点有两条路径，其中一条的成功概率为 0.2 ，而另一条为 0.5 * 0.5 = 0.25

 使用dfs，对每一个边进行遍历，直至遇到end，取当前的权值积res与历史权重积ans最值，ans=max(ans,res)。但是会超时，

9 / 16 个通过测试用例。

struct E{int v;double c;
};class Solution {
public:vector<vector<E>> e;vector<bool> mark;double ans;void dfs(int x, int end, double res){if(x == end) {ans = max(ans, res);return;}for(int i = 0; i < e[x].size(); i++){int next = e[x][i].v;double cost = e[x][i].c;if(!mark[next]){mark[next] = true;dfs(next, end, res * cost);mark[next] = false;}}}double maxProbability(int n, vector<vector<int>>& edges, vector<double>& w, int start, int end) {//邻接链表存图e.resize(n);mark.resize(n, false);E tmp;for(int i = 0; i < edges.size(); i++){tmp.c = w[i];tmp.v = edges[i][0];e[edges[i][1]].push_back(tmp);tmp.v = edges[i][1];e[edges[i][0]].push_back(tmp);}mark[start] = true;ans = 0.0;dfs(start, end, 1.0);return ans;}
};

修改：我自己想出来的~用BFS，从cur点，每找一个相邻点next，判断此时到next的概率是否为最大，res[next]存到next的概率，初始化为0，当res[next] < res[cur] * cost，证明此时到next的最大概率更新了，需要重新入队列，更新与next相连的点的概率！！

struct E{int v;double c;
};class Solution {
public:vector<vector<E>> e;double maxProbability(int n, vector<vector<int>>& edges, vector<double>& w, int start, int end) {//邻接链表存图e.resize(n);E tmp;for(int i = 0; i < edges.size(); i++){tmp.c = w[i];tmp.v = edges[i][0];e[edges[i][1]].push_back(tmp);tmp.v = edges[i][1];e[edges[i][0]].push_back(tmp);}// BFSvector<double> res(n, 0.0); // 到i点的最大概率值queue<int> q;q.push(start);res[start] = 1.0;while(!q.empty()){int cur = q.front();q.pop();for(int i = 0; i < e[cur].size(); i++){int next = e[cur][i].v;double cost = e[cur][i].c;if(res[next] < res[cur] * cost){res[next] = res[cur] * cost;q.push(next);} }}return res[end];}
};

结果：

执行用时：408 ms, 在所有 C++ 提交中击败了88.24% 的用户

内存消耗：65.9 MB, 在所有 C++ 提交中击败了100.00% 的用户

 

三分查找

1515、一家快递公司希望在新城市建立新的服务中心。公司统计了该城市所有客户在二维地图上的坐标，并希望能够以此为依据为新的服务中心选址：使服务中心 到所有客户的欧几里得距离的总和最小 。

给你一个数组 positions ，其中 positions[i] = [xi, yi] 表示第 i 个客户在二维地图上的位置，返回到所有客户的 欧几里得距离的最小总和 。

换句话说，请你为服务中心选址，该位置的坐标 [xcentre, ycentre] 需要使下面的公式取到最小值：

与真实值误差在 10^-5 之内的答案将被视作正确答案。

示例 1：

输入：positions = [[0,1],[1,0],[1,2],[2,1]]
输出：4.00000
解释：如图所示，你可以选 [xcentre, ycentre] = [1, 1] 作为新中心的位置，这样一来到每个客户的距离就都是 1，所有距离之和为 4 ，这也是可以找到的最小值。

三分查找：一个 R上的凸函数 y=f(x)，定义域为 [L,R]，用三分查找的方式将不可能包含最小值点的范围排除：

（1）取两个点 x1,x2，满足 L<x1<x2<R，记 y1=f(x1)，y2=f(x2)；

（2）如果 y1>y2​，那么最小值点一定不在 [L,x1] 内；如果 y1<y2，那么最小值点一定不在 [x2,R]内。

 

题目中的函数 f(xc,yc)是二元函数，我们可以使用「三分查找」套「三分查找」的方法。外层的三分查找用来确定 xc的范围，每次三分查找时，取定义域 [xL,xR]中的两个三等分点 x1,x2​，并分别固定 xc的值为 x1和 x2，对 yc​ 进行三分查找。

取 x1,x2​ 为 [L,R] 的三等分点，即：

每次就可以排除三分之一的定义域。当定义域的宽度 R−L 收敛至给定的阈值 ϵ时，就可以结束三分查找。此时 L 和 R 足够接近，可以将 [L,R]内的所有值都视作极值点。

 // 此处不加&，会超时
  for(auto &p:pos)

const double EPS = 5e-6;    // 误差阈值,视left和left + EPS有相同的性质
const double INF = 1e9;class Solution {
public:double dist(double x, double y, vector<vector<int>>& pos){double ans = 0;// 此处不加&，会超时for(auto &p:pos)   // 对vector使用迭代器遍历，注意&p,有一个引用号&ans += sqrt((x - p[0]) * (x - p[0]) + (y - p[1]) * (y - p[1]));return ans;}// 确定x值，对y方向三分查找最值double caly(double x, vector<vector<int>>& pos){double ans = INF;int l = pos[0][1], r = pos[0][1];// 此处不加&，会超时for(auto &p:pos) l = min(l, p[1]), r = max(r, p[1]);double left = l - EPS, right = r + EPS;while(left + EPS < right){double y1 = left + (right - left) / 3.0;double y2 = right - (right - left) / 3.0;double ans1 = dist(x, y1, pos);double ans2 = dist(x, y2, pos);ans = min(ans, min(ans1, ans2));if(ans1 > ans2) left = y1;else right = y2;}return ans;}double getMinDistSum(vector<vector<int>>& pos) {double ans = INF;int l = pos[0][0], r = pos[0][0];// 找x取值范围[left, right]  // 此处不加&，会超时for(auto &p:pos) l = min(l, p[0]), r = max(r, p[0]); // min(double, int)没有这样的函数，只能比较int--> min(int,int)double left = l - EPS, right = r + EPS;while(left + EPS < right){double x1 = left + (right - left) / 3.0;double x2 = right - (right - left) / 3.0;double y1min = caly(x1, pos);double y2min = caly(x2, pos);ans = min(ans, min(y1min, y2min));if(y1min < y2min) right = x2;else left = x1;}return ans;}
};

结果：

执行用时：268 ms, 在所有 C++ 提交中击败了41.47% 的用户

内存消耗：8 MB, 在所有 C++ 提交中击败了100.00%