一.前缀和

1.前缀和介绍

2.编程中的前缀和

二.一维数组的动态和

1.题目描述

2.问题分析

3.代码实现

三.除自身以外数组的乘积

1.题目描述

2.问题分析

3.代码实现

四.和为 K 的子数组

1.题目描述

2.问题分析

3.代码实现

五.形成两个异或相等数组的三元组数目

1.题目描述

2.问题分析

3.代码实现

一.前缀和

1.前缀和介绍

前缀和,顾名思义,就是前n项相加之和,和我们高中时候学习的数列中的 $S_{n}$ 一个含义

例如一个等差数组 $a_{n}$ =n,那他的前n项和 $S_{n}$ = $\frac{n*(n+1)}{2}$

也可知道 $S_{n}$ - $S_{n-1}$ = $a_{n}$

2.编程中的前缀和

对于一个数组nums,也可以很容易求出它的前缀和数组

    public int[] prefix(int[] nums) {int[] prefix = new int[nums.length];prefix[0] = nums[0];for (int i = 1; i < nums.length; ++i) {prefix[i] = prefix[i - 1] + nums[i];}return prefix;}

prefix数组的含义是: prefix[i]的值为nums数组从0到i的元素之和

其实我们这里的前缀和并不仅仅局限于前几项的和,之后我们还会涉及到乘法前缀和(后缀和),异或前缀和等等......并且还会存在后缀和的情况

二.一维数组的动态和

1.题目描述

给你一个数组 nums 。数组「动态和」的计算公式为：runningSum[i] = sum(nums[0]…nums[i]) 。

请返回 nums 的动态和。

力扣:力扣

2.问题分析

这道题就是一道典型的前缀和题目,没什么特别之处,数组的动态和计算公式就是前缀和的含义,可以直接写出代码求解

3.代码实现

    public int[] runningSum(int[] nums) {int[] prefix = new int[nums.length];prefix[0] = nums[0];for (int i = 1; i < nums.length; ++i) {prefix[i] = prefix[i - 1] + nums[i];}return prefix;}

三.除自身以外数组的乘积

1.题目描述

给你一个整数数组 nums，返回 数组 answer ，其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。

题目数据保证数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。

请不要使用除法，且在 O(n) 时间复杂度内完成此题。

力扣:力扣

2.问题分析

这个问题说的很明白,不能用除法来进行,我们的第一想法是使用乘法前缀和来进行计算,但是考虑到不能使用除法和数组中可能存在0,所以这样是不能够满足题意和解答问题的.

因此我们不妨再来设置一个数组,这个数组用来存储乘法后缀和,我们计算res[i]的时候就可以它的前缀和乘以它的后缀和,这样它的结果就可以求出来了

设置前缀和数组left[i]含义为:从nums数组的第0到第i-1项的叠乘所获得的结果

设置后缀和数组right[i]含义为:从nums数组的第i+1到最后一项项的叠乘所获得的结果

最后结果数组res[i]=left[i]*right[i]

3.代码实现

    public int[] productExceptSelf(int[] nums) {int[] left = new int[nums.length];//left[i]:从0-i-1项相乘int[] right = new int[nums.length];//right[i]:从i+1到最后一项相乘left[0] = 1;right[nums.length - 1] = 1;for (int i = 1; i < nums.length; ++i) {left[i] = left[i - 1] * nums[i - 1];}for (int j = nums.length - 2; j >= 0; --j) {right[j] = right[j + 1] * nums[j + 1];}int[] res = new int[nums.length];for (int i = 0; i < nums.length; ++i) {res[i] = left[i] * right[i];}return res;}

四.和为 K 的子数组

1.题目描述

给你一个整数数组 nums 和一个整数 k ，请你统计并返回 该数组中和为 k 的连续子数组的个数 。

力扣:力扣

2.问题分析

这一题我们不妨先暴力思考一下,暴力就是把它的所有子数组的和全部求出来,然后和k进行判断,最后统计出等于k的子数组的数量,至少也进行两层for循环,代码如下:

    public int subarraySum(int[] nums, int k) {int count = 0;for (int end = 0; end < nums.length; ++end) {int sum = 0;for (int start = end; start >= 0; --start) {sum += nums[start];if (sum == k) {count++;}}}return count;  }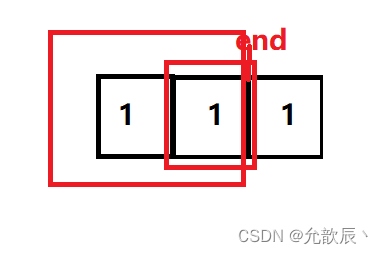

相当于外层循环确定end,内层循环确定开始的位置start的位置

其实我们可以用一个哈希表进行优化,因为它的前缀和每次都是叠加的,其实只要统计它的每个前缀和的次数,然后prefix-k就是它从0到start的前缀和,此时start+1到end的位置就是和为k的子数组,同时map哈希表刚开始的时候还要添加key=0,value=1的键值对,因为当prefix刚好为k的时候,prefix-k=0,表示从0到end的子数组符合条件

3.代码实现

    public int subarraySum(int[] nums, int k) {HashMap<Integer, Integer> map = new HashMap<>();map.put(0, 1);//此时是从0到i的前缀和int prefix = 0, count = 0;for (int end = 0; end  < nums.length; ++end ) {prefix += nums[end];if (map.containsKey(prefix - k)) {count += map.get(prefix - k);}map.put(prefix, map.getOrDefault(prefix, 0) + 1);}return count;        }

五.形成两个异或相等数组的三元组数目

1.题目描述

给你一个整数数组 arr 。

现需要从数组中取三个下标 i、j 和 k ，其中 (0 <= i < j <= k < arr.length) 。

a 和 b 定义如下：

a = arr[i] ^ arr[i + 1] ^ ... ^ arr[j - 1]
b = arr[j] ^ arr[j + 1] ^ ... ^ arr[k]
注意：^ 表示 按位异或 操作。

请返回能够令 a == b 成立的三元组 (i, j , k) 的数目。

力扣:力扣

2.问题分析

首先我们想的就是需要暴力遍历i,j和k这三个值,这一题是异或前缀和,首先我们把它的异或前缀和数组求解出来,然后用异或前缀和来表达a和b,

前缀和数组prefixArr[i]的含义:nums从0到i-1的异或前缀

a=prefixArr[j]^prefixArr[i]

b=prefixArr[k+1]^prefixArr[j]

a==b 即 prefixArr[k+1]==prefixArr[i]

知道这个之后,我们就可以使用暴力的方法求解出满足条件的三元组的数量了

3.代码实现

    public int countTriplets(int[] arr) {int[] prefixArr = new int[arr.length + 1];for (int i = 1; i <= arr.length; ++i) {prefixArr[i] = prefixArr[i - 1] ^ arr[i - 1];}System.out.println(Arrays.toString(prefixArr));int count = 0;for (int i = 0; i < arr.length - 2; ++i) {for (int j = i + 1; j < arr.length - 1; ++j) {for (int k = j + 1; k < arr.length; ++k) {if (prefixArr[k + 1] == prefixArr[i])count++;}}}return count;}