题目链接

http://oj.daimayuan.top/problem/436

题面

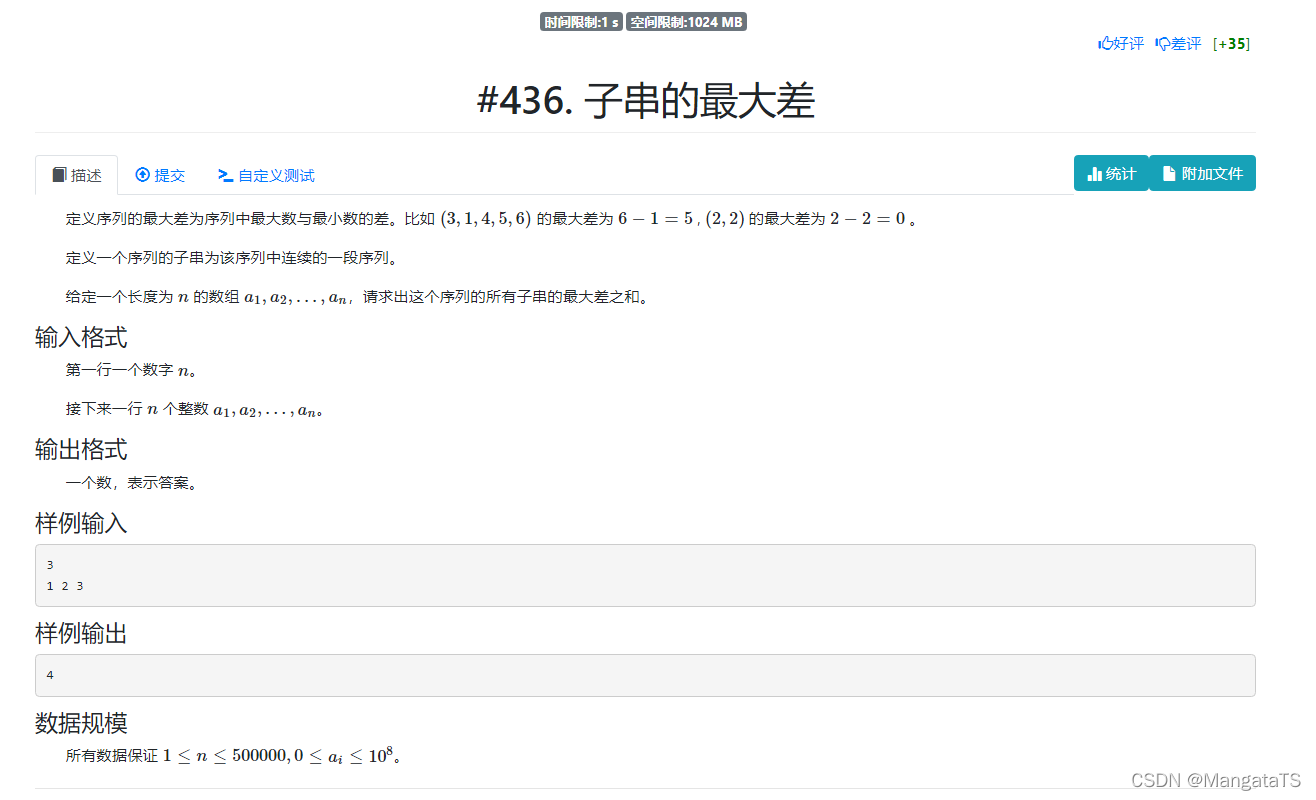
思路

我们考虑每一个点作为一个区间最小值和区间最大值的次数，那么我们可以从两边延申，对于区间最小值而言找到左边第一个大于自身的数，对于右边也找到大于第一个大于自身的数，那么这两个区间长度的积就是我们区间以当前为最小值的次数，很显然这个值可以通过单调栈维护，那么我们分别从左往右和从右往左用两个单调栈维护，注意只有一个地方取=即可，同理可以将每个点作为区间最大值的次数统计起来，统计完信息后我们从左往右将每个点的权值计算在ans里即可，即：
$ans+=a[i]\ast (lmax[i]\ast rmax[i]-lmin[i]\ast rmin[i])$

代码

#include<bits/stdc++.h>
using namespace std;
//----------------自定义部分----------------
#define ll long long
#define mod 1000000007
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3fint dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};ll ksm(ll a,ll b) {ll ans = 1;for(;b;b>>=1LL) {if(b & 1) ans = ans * a % mod;a = a * a % mod;}return ans;
}ll lowbit(ll x){return -x & x;}const int N = 2e6+10;
//----------------自定义部分----------------
ll t,n,m,q,a[N],b[N],lmin[N],rmin[N],lmax[N],rmax[N];
void slove(){cin>>n;for(int i = 1;i <= n; ++i) cin>>a[i],b[i] = a[i];reverse(b+1,b+n+1);stack<int> S;//找每个数作为min被调用多少次//左半边for(int i = 1;i <= n; ++i) {while(S.size() && a[S.top()] >= a[i]) S.pop();if(S.size()) lmin[i] = i - S.top();else lmin[i] = i;S.push(i);}//右半边while(S.size()) S.pop();for(int i = n;i >= 1; --i) {while(S.size() && a[S.top()] > a[i]) S.pop();if(S.size()) rmin[i] = S.top() - i;else rmin[i] = n - i + 1;S.push(i);}//找每个数作为max被调用多少次while(S.size()) S.pop();for(int i = 1;i <= n; ++i) {while(S.size() && a[S.top()] <= a[i]) S.pop();if(S.size()) lmax[i] = i - S.top();else lmax[i] = i;S.push(i);}while(S.size()) S.pop();for(int i = n;i >= 1; --i) {while(S.size() && a[S.top()] < a[i]) S.pop();if(S.size()) rmax[i] = S.top() - i;else rmax[i] = n - i + 1;S.push(i);}ll ans = 0LL;for(int i = 1;i <= n; ++i)ans += a[i] * (lmax[i] * rmax[i] - lmin[i] * rmin[i]);cout<<ans<<endl;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);t = 1;while(t--){slove();}return 0;
}