在雷达系统中,目标检测是一项非常重要的任务。检测本身非常简单,它将信号与阈值进行比较,超过阈值的信号则认为是目标信号,所以目标检测的真正工作是寻找适当的阈值。由于目标误检的严重后果,因此雷达系统希望有一个检测阈值,该阈值不仅能最大限度地提高检出概率,而且能将误报概率保持在预设水平以下。
有大量的文献对使用多个接收信号样本检测高斯白噪声中的信号的情况进行了分析,并获得了一些众所周知的结果,然而,所有这些经典结果都基于理论概率,并且仅限于具有已知方差与期望的高斯白噪声。在实际应用中,噪声通常是有色的,其功率是未知的🌒。
本文介绍了雷达编程中常会遇到的目标检测技术---CFAR(Constant False-Alarm Rate),还是笔者的老习惯,先来过一下文中涉及的一些公式以及解释📌。
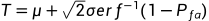 ,这个公式我们后边称为公式一,它计算具有已知方差与期望的高斯白噪声符合虚警概率为
,这个公式我们后边称为公式一,它计算具有已知方差与期望的高斯白噪声符合虚警概率为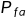 的阈值T。
的阈值T。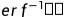 是
是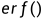 的反函数,erf可在matlab中直接使用,定义是
的反函数,erf可在matlab中直接使用,定义是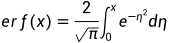 ,
,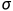 是噪声的标准差,
是噪声的标准差,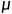 是数学期望,而
是数学期望,而 为阈值。
为阈值。
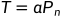 ,这个公式我们称之为公式二,它反映了阈值与根据给定的检测窗口(CUT)估计出来的噪声功率
,这个公式我们称之为公式二,它反映了阈值与根据给定的检测窗口(CUT)估计出来的噪声功率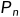 以及虚警概率之间的关系。
以及虚警概率之间的关系。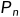 常为检测窗口的均值,表示为
常为检测窗口的均值,表示为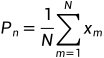 。假设传入检测系统的脉冲为单个脉冲(不涉及脉冲积分),则
。假设传入检测系统的脉冲为单个脉冲(不涉及脉冲积分),则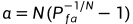 ,其中
,其中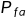 为虚警概率,N为估计检测窗口的大小。
为虚警概率,N为估计检测窗口的大小。
恒定阈值即指提前对传入检测系统的噪声参数进行估计,并根据一定的虚警概率计算出一个恒定的阈值,在目标检测时大于预设的阈值即判断为有目标。然而,当雷达接收机输出到检测系统的噪声发生变化时(比如功率的变化),检测系统无法做出适当的调整,将会导致实际的虚警率发生了变化。
在雷达信号检测中,当外界噪声强度变化时,雷达能自动调整其目标检测阈值,使雷达的虚警概率保持不变,具有这种特性的检测手段称为恒虚警率检测。
基础理论知识
检测的作用就是在含有噪声的情况下确定目标的存在和不存在。在我们不知道目标是否存在的情况下,目标检测的工作就变成了针对两种可能假设的概率,来对当前的信号做出判决。
一种叫原假设,也叫零假设,用H0表示,我们针对雷达系统理解为噪声,另外一种叫备择假设,用H1表示,理解为目标。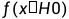 表示当功率x为噪声的功率,
表示当功率x为噪声的功率,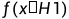 表示当输入信号功率x为信号的概率。Critial value为决策边界(判断阈值),大于边界(阈值)的我们认为是目标,而小于阈值的我们认为是噪声。因为我们的原假设是噪声,所以对应的接受区域在下图左侧,拒绝区域在下图右侧。对应的假拒绝概率(虚警概率)与假接收概率(漏检概率)如下图所示。
表示当输入信号功率x为信号的概率。Critial value为决策边界(判断阈值),大于边界(阈值)的我们认为是目标,而小于阈值的我们认为是噪声。因为我们的原假设是噪声,所以对应的接受区域在下图左侧,拒绝区域在下图右侧。对应的假拒绝概率(虚警概率)与假接收概率(漏检概率)如下图所示。
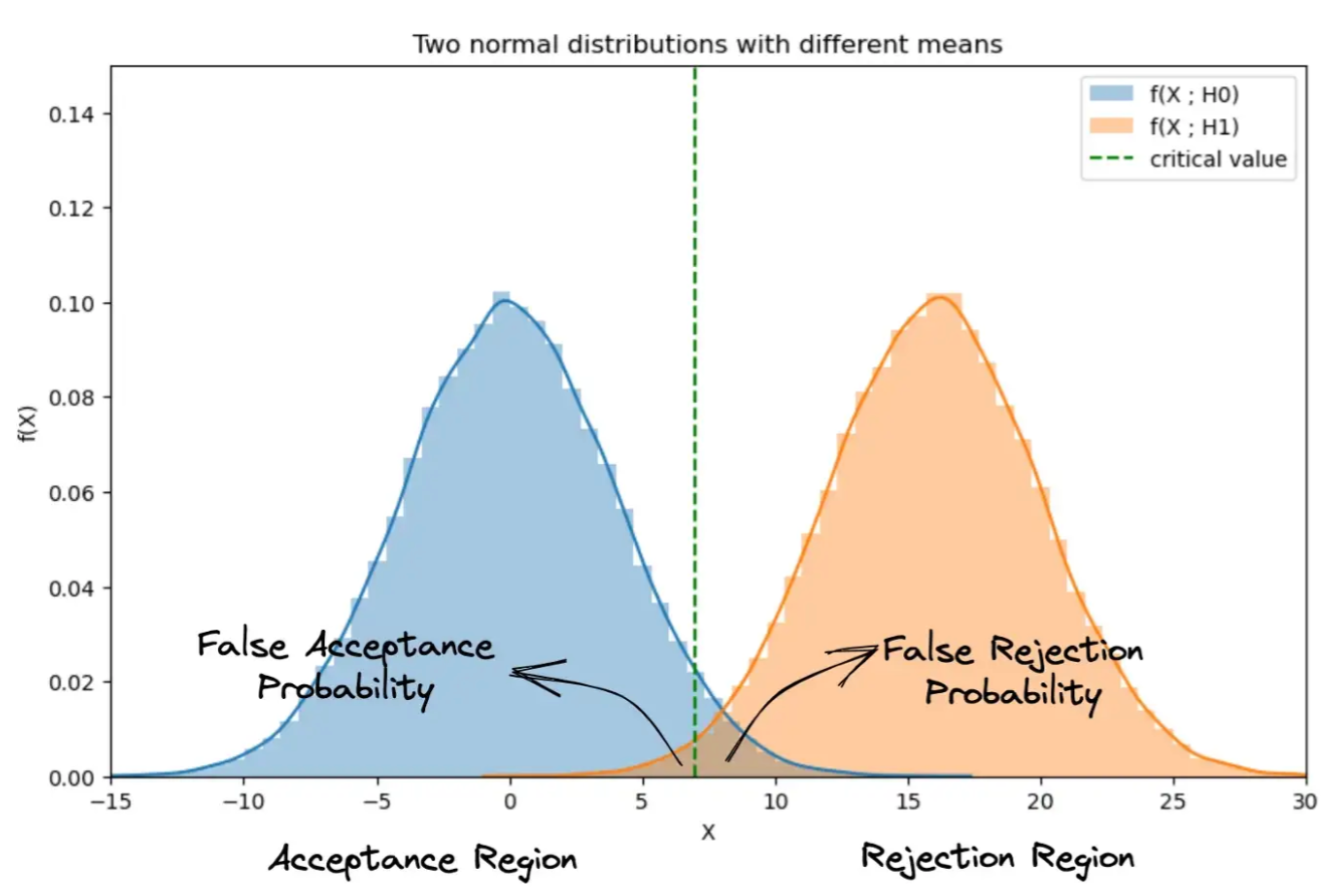
从雷达接收机输入到检测系统的信号是目标信号+噪声,如下图中的实线,我们可以计算噪声回波信号的统计特性,将噪声的概率密度函数也画出,如下图的虚线,然后根据确定的虚警概率,我们就可以知道检测阈值的大小,这也是恒定阈值法的基本思路。
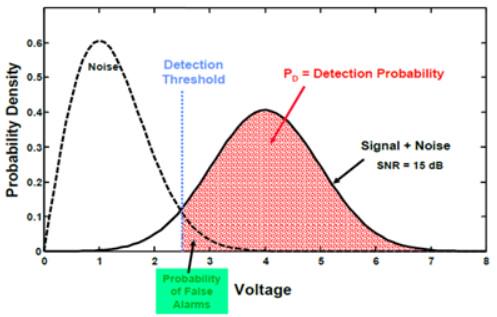
我们假设噪声是高斯白噪声,功率表现符合高斯分布。通过计算噪声的统计特性之后,就可以通过公式一计算出相关的阈值。这个是恒定阈值的目标检测。而我们的噪声一般是有色的(不是纯的随机数,有一定相关性),功率的期望也是未知的。为了解决这个问题,我们先复习一下高斯分布与标准差之间的关系。
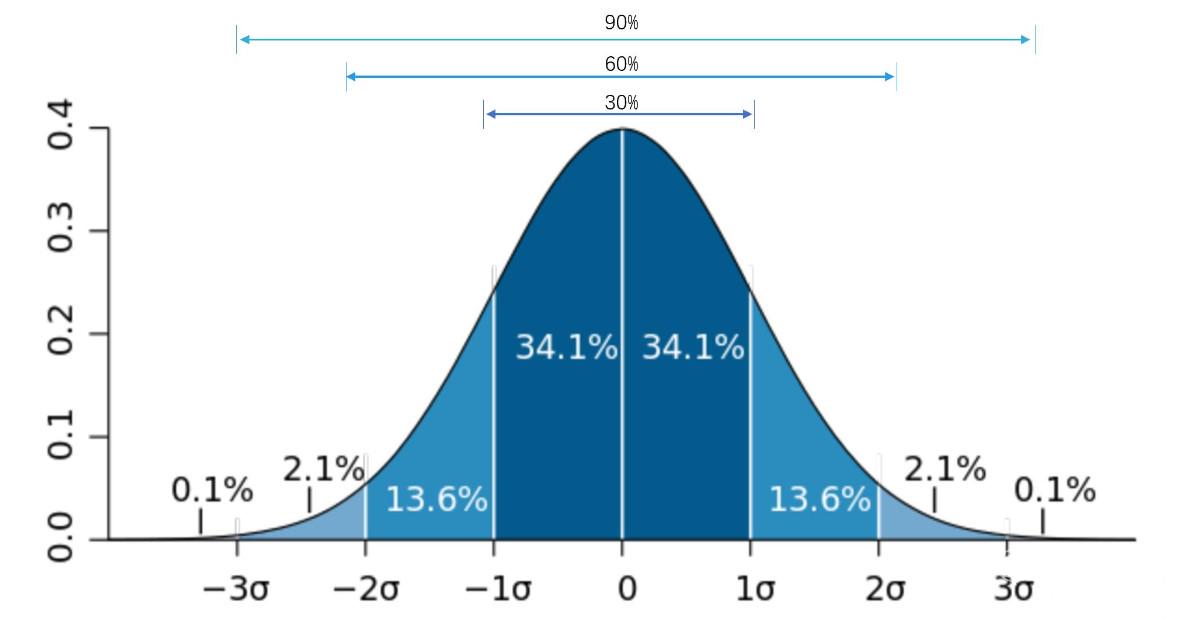
我们可以将这种有色,功率未知的噪声信号理解成很多个符合正态分布,但是具有不同统计特性的噪声拼接而成。我们根据上图可以看出,符合高斯分布的噪声概率分布与噪声的统计特性诸如标准差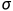 和数学期望
和数学期望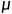 都有关系,也就是说,我们可以根据噪声的统计特性来表示一个符合确定虚警率的阈值,
都有关系,也就是说,我们可以根据噪声的统计特性来表示一个符合确定虚警率的阈值,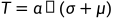 ,这就是我们公式公式2的由来,我们通过把噪声切割成具有一定尺寸的窗口来获得当前检测单元的阈值,即每一个检测单元都对应一个根据周围单元估算出的噪声统计特性再乘以一个由虚警概率确定的
,这就是我们公式公式2的由来,我们通过把噪声切割成具有一定尺寸的窗口来获得当前检测单元的阈值,即每一个检测单元都对应一个根据周围单元估算出的噪声统计特性再乘以一个由虚警概率确定的 算出的判决阈值。所以对于CFAR,我们的阈值不是个定值,而是如下图一个蓝色曲线。
算出的判决阈值。所以对于CFAR,我们的阈值不是个定值,而是如下图一个蓝色曲线。
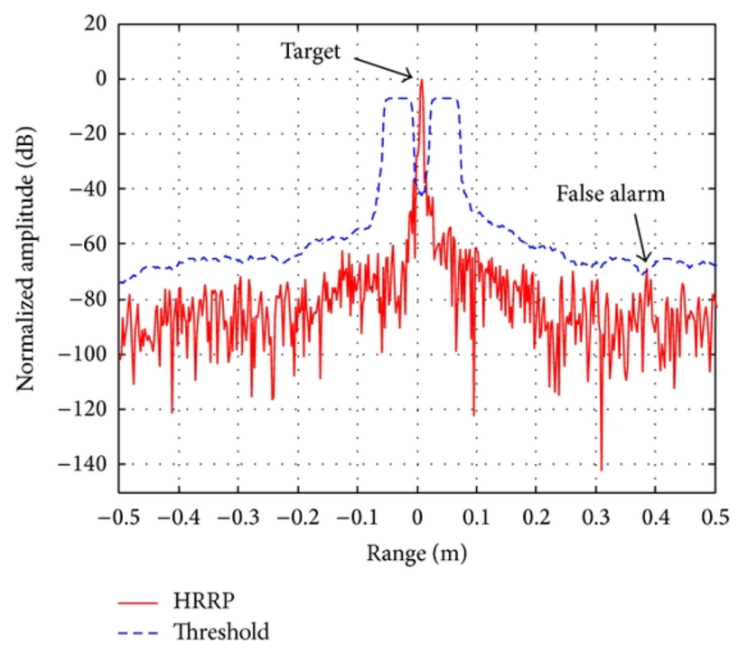
雷达一维恒虚警多算法Matlab实现
背景噪声生成函数
下面这个function主要实现了根据输入的统计特性输出符合高斯分布的均匀背景噪声矩阵,输入的参数包括标准差,噪声点数,平均dB,以及是否将噪声画出来的开关量。输出噪声一维矩阵。
在这里先说明一个dB的概念,dB表示的是系统的输出功率相对输入功率的增益。这里dB的引入是为了把乘除关系变换为加减,便于工程中的运算。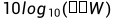 ,后边的Matlab程序传递的参数,都将功率值转换为了dB.
,后边的Matlab程序传递的参数,都将功率值转换为了dB.
%均匀背景噪声
function [ xc ] = env_uniform(variance, shape, power_db, show_out)c=10^(power_db/10); % power_db这里是幅度对应功率tes=random('Normal',0,variance,1,shape);xc=c + tes; if show_out==1plot(10.*log10(abs(xc)));end
end下面这个function也是输出噪声矩阵,只不过输出的噪声类型是杂波边缘背景噪声,即由多个不同均值的的噪声拼接而成,因此输入的平均dB也是一个具有多个元素的一维向量。
%杂波边缘背景噪声
function [ xc ] = env_edge(variance, shape, power_db, show_out)c=10.^(power_db./10); % 这里是幅度——功率xc=random('Normal',0,variance,1,shape(1,end)); xc(1,1:end)=xc(1,1:end)+c(1,1);index=1;for i=1:length(power_db)xc(1,index:shape(1,i))=xc(1,index:shape(1,i)).*c(1,i)./c(1,1);index=shape(1,i)+1;endif show_out==1plot(20.*log10(abs(xc)));end
end恒虚警率算法
到了最重要的CFAR算法实现了,本篇文章讨论最常见的均值类算法,核心思想是通过对参考窗内采样数据取平均来估计背景噪声功率。被检测单元由保护单元与训练单元所包围,保护单元不参与计算噪声平均功率。算法利用保护单元计算平均功率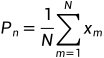 ,然后再乘以用虚警概率确定的系数
,然后再乘以用虚警概率确定的系数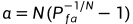 ,最终得出针对当前检测单元的判决阈值。
,最终得出针对当前检测单元的判决阈值。
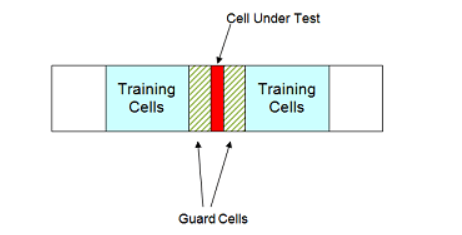
CA-CFAR、GO-CFAR、SO-CFAR算法这三个是最经典的均值类CFAR算法,后续有其变形log-CFAR算法但是原理是相同的👀。
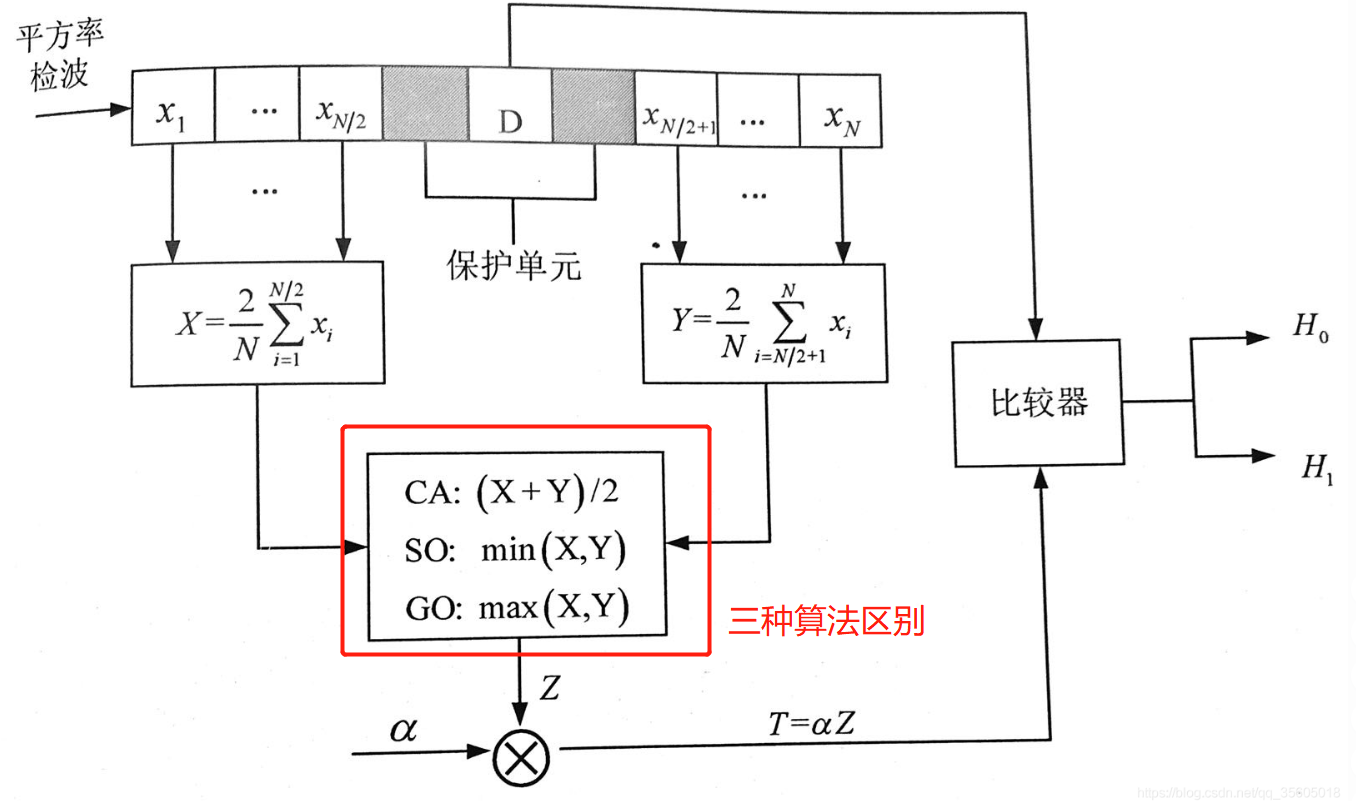
下面是这三种算法的Matlab实现,输入信号,训练单元数,保护单元数,以及恒定的虚警概率,输出与信号尺寸一样的阈值曲线。
function [ index, XT ] = cfar_ac( xc, N, pro_N, PAF)alpha=N.*(PAF.^(-1./N)-1);index=1+N/2+pro_N/2:length(xc)-N/2-pro_N/2;XT=zeros(1,length(index));for i=indexcell_left=xc(1,i-N/2-pro_N/2:i-pro_N/2-1);cell_right=xc(1,i+pro_N/2+1:i+N/2+pro_N/2);Z=(sum(cell_left)+sum(cell_right))./N;XT(1,i-N/2-pro_N/2)=Z.*alpha;end
endfunction [ index, XT ] = cfar_go( xc, N, pro_N, PAF)alpha=N.*(PAF.^(-1./N)-1);index=1+N/2+pro_N/2:length(xc)-N/2-pro_N/2;XT=zeros(1,length(index));for i=indexcell_left=xc(1,i-N/2-pro_N/2:i-pro_N/2-1);cell_right=xc(1,i+pro_N/2+1:i+N/2+pro_N/2);Z=max([mean(cell_left),mean(cell_right)]);XT(1,i-N/2-pro_N/2)=Z.*alpha;end
endfunction [ index, XT ] = cfar_so( xc, N, pro_N, PAF)alpha=N.*(PAF.^(-1./N)-1);index=1+N/2+pro_N/2:length(xc)-N/2-pro_N/2;XT=zeros(1,length(index));for i=indexcell_left=xc(1,i-N/2-pro_N/2:i-pro_N/2-1);cell_right=xc(1,i+pro_N/2+1:i+N/2+pro_N/2);Z=min([mean(cell_left),mean(cell_right)]);XT(1,i-N/2-pro_N/2)=Z.*alpha;end
end三种算法在目标检测方面各有优缺点,总结如下表🔢:
算法名称 | 优点 | 缺点 |
CA-CFAR(单元平均恒虚警) | 损失率最少的一种算法 | 多目标遮掩,杂波边缘性能也欠佳 |
GO-CFAR(最大选择恒虚警) | 杂波边缘区域虚警概率降低 | 多目标遮掩 |
SO-CFAR(最小选择恒虚警) | 多目标效果有改进; | 杂波边缘区域虚警概率提升 |
算法测试程序
最后要讲述的Matlab程序,是一段针对这三个算法其中一个算法的测试程序。程序模拟单目标,使用均匀噪声背景,噪声20dB,目标的信噪比是15dB。程序使用之前介绍的Function,最终画出信号曲线与阈值曲线。
clc
clear all
close allshape=[200];
variance=200;
noise_db=20;
noise_p=10.^(noise_db./10);
show_out=0;
[ xc ] = env_uniform(variance, shape, noise_db,show_out);SNR1=15; signal1_p=10.^(SNR1./10).*noise_p;
xc(1,90)=signal1_p;
N=36;
pro_N=2;
PAF=10^(-4);
[ index, XT ] = cfar_so( abs(xc), N, pro_N, PAF);
%[ index, XT ] = cfar_go( abs(xc), N, pro_N, PAF);
%[ index, XT ] = cfar_ac( abs(xc), N, pro_N, PAF);figure(3);
plot(10.*log10(abs(xc))),hold on;
plot(index,10.*log10(abs(XT))),hold on;
legend('噪声pdf','信号pdf')Matlab程序执行结果如下:
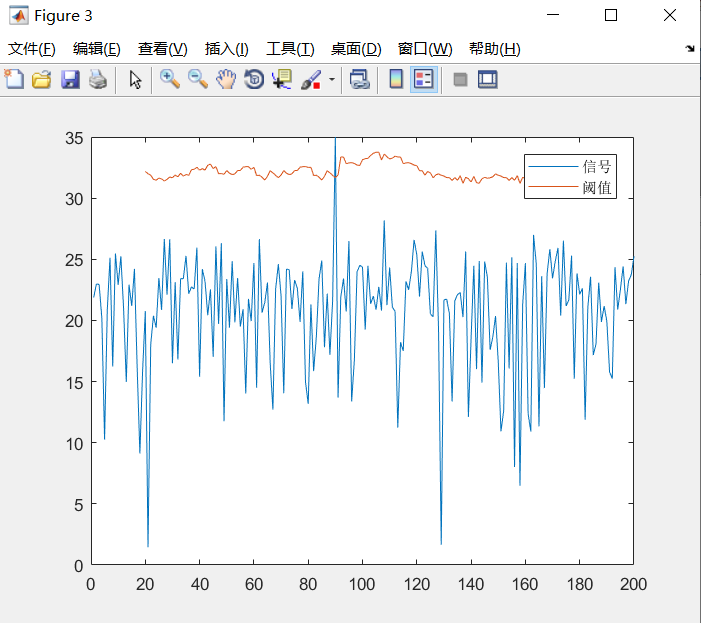
我们还可以针对杂波边缘背景噪声来试验不同算法在杂波的边缘的性能,我们也可以往噪声中多叠加一些不同信噪比的目标来观察不同算法在多目标情况下的效果。点击这里跳转到一个github上一个利用MATLAB GUI设计平台,设计多算法雷达一维恒虚警检测CFAR可视化界面的项目代码。
加速核嵌入式软件配置
下面的某平台针对Cfar加速核的配置代码段:
void BB_CFAR_Init(void){cfarCfg0_st.wrapDirA = CFAR_CFG0_WRAPDIR_INC;cfarCfg0_st.wrapDirB = CFAR_CFG0_WRAPDIR_INC;cfarCfg0_st.sumMode = CFAR_CFG0_SUMMODE_ABS;cfarCfg0_st.interCnt = USE_RANGE;cfarCfg0_st.intraCnt = NUM_VEL;cfarCfg0_st.thresDiv = CFAR_CFG0_THRESDIV4; // = searchSize numcfarCfg0_st.divFac = CFAR_CFG0_DIVFAC1;cfarCfg0_st.mulFac = r2_str.cfarThV;cfarCfg0_st.searchSize = r2_str.cfarThVS;cfarCfg0_st.guardSize = r2_str.cfarThVG;cfarCfg0_st.totalSize = cfarCfg0_st.searchSize+cfarCfg0_st.guardSize;cfarCfg0_st.pdEn = CFAR_CFG0_PEAKDET_DIS; cfarCfg0_st.cfarMode = CFAR_CFG0_CFARMODE_GO;BB_CFAR_CFG0(&cfarCfg0_st); //STRUCT_CFAR_CFG0BB_CFAR_CFG1(CFAR_MAX_NUM,NUM_BYTE32); //interIncBB_CFAR_CFG2(bb_prep.cfg2.jumpInc,FFT2D_CACHE_ADDR+USE_RANGE*CFAR_ANT*NUM_BYTE32);//intraInc,intraAddrBB_CFAR_CFG3((FFT2D_CACHE_ADDR+USE_RANGE*CFAR_ANT*NUM_BYTE32+(NUM_VEL-cfarCfg0_st.totalSize)*bb_prep.cfg2.jumpInc),FFT2D_CACHE_ADDR+USE_RANGE*CFAR_ANT*NUM_BYTE32);//wrapAddrA,wrapAddrBBB_CFAR_CFG4(CFAR_CACHE_ADDR);//dstBaseAddr
}其中searchSize 对应的是训练单元的大小,guardSize是保护单元,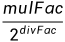 等于上面Matlab程序中的alpha,即阈值系数。
等于上面Matlab程序中的alpha,即阈值系数。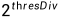 需要与searchSize保持一致。加速核支持不同算法的选择,这里cfarMode选择的是GO-CFAR。
需要与searchSize保持一致。加速核支持不同算法的选择,这里cfarMode选择的是GO-CFAR。
此平台默认的将采样的窗口滑动的模式配置称为环状,即第一个检测点的左窗由信号末尾部分充当,最后一个检测点的右窗由信号的起始部分充当。
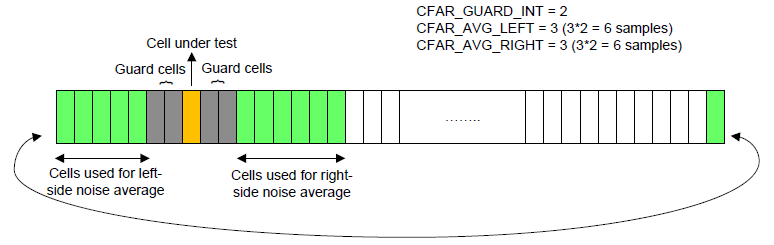
最后,我们可能会针对项目的技术需求调整CFAR的参数,这就需要我们知道这些参数和一些概念相互如何影响,下面简单的总结一些参数调整的影响。
检测单元数N:在相同信噪比下,检测单元数越多的CFAR对应的检测概率越高,但同时计算量加大。
保护单元数:保护单元过大或过小都会使检测概率降低,应不同实验选取适中的保护单元数。
虚警概率
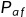 :在相同检测单元数目下,虚警概率的越高CFAR对应的检测概率越高,但虚警数也增多。
:在相同检测单元数目下,虚警概率的越高CFAR对应的检测概率越高,但虚警数也增多。
信噪比SNR:当信噪比不断增加,检测概率也不断增加。