算法修炼之筑基篇——筑基一层初期（解决01背包问题）

✨博主：命运之光

✨专栏：算法修炼之练气篇

✨博主的其他文章：点击进入博主的主页

前言：学习了算法修炼之练气篇想必各位蒟蒻们的基础已经非常的扎实了，下来我们进阶到算法修炼之筑基篇的学习。筑基期和练气期难度可谓是天差地别，懂得都懂，题目难度相比起练气期的题目难度提升很多，所以要是各位蒟蒻小伙伴们看不懂筑基期的题目可以在练气期多积累积累，练气期的题目也会不断更新，大家一定要把基础打牢固了再来看筑基期的题目哈，这样子也可以提高大家的学习效率，一举两得，加油(●'◡'●)🎉🎉

✨经典的01背包问题

🍓小明的背包1

🍓解题代码

🍓dp数组打表如下：

编辑 ✨经典01背包问题的解题思路

✨01背包的递推公式（重要需要记忆）

✨01背包的递推公式优化为一维数组（重要需要记忆）

✨经典的01背包问题

让我们先看一道经典的01背包问题

🍓小明的背包1

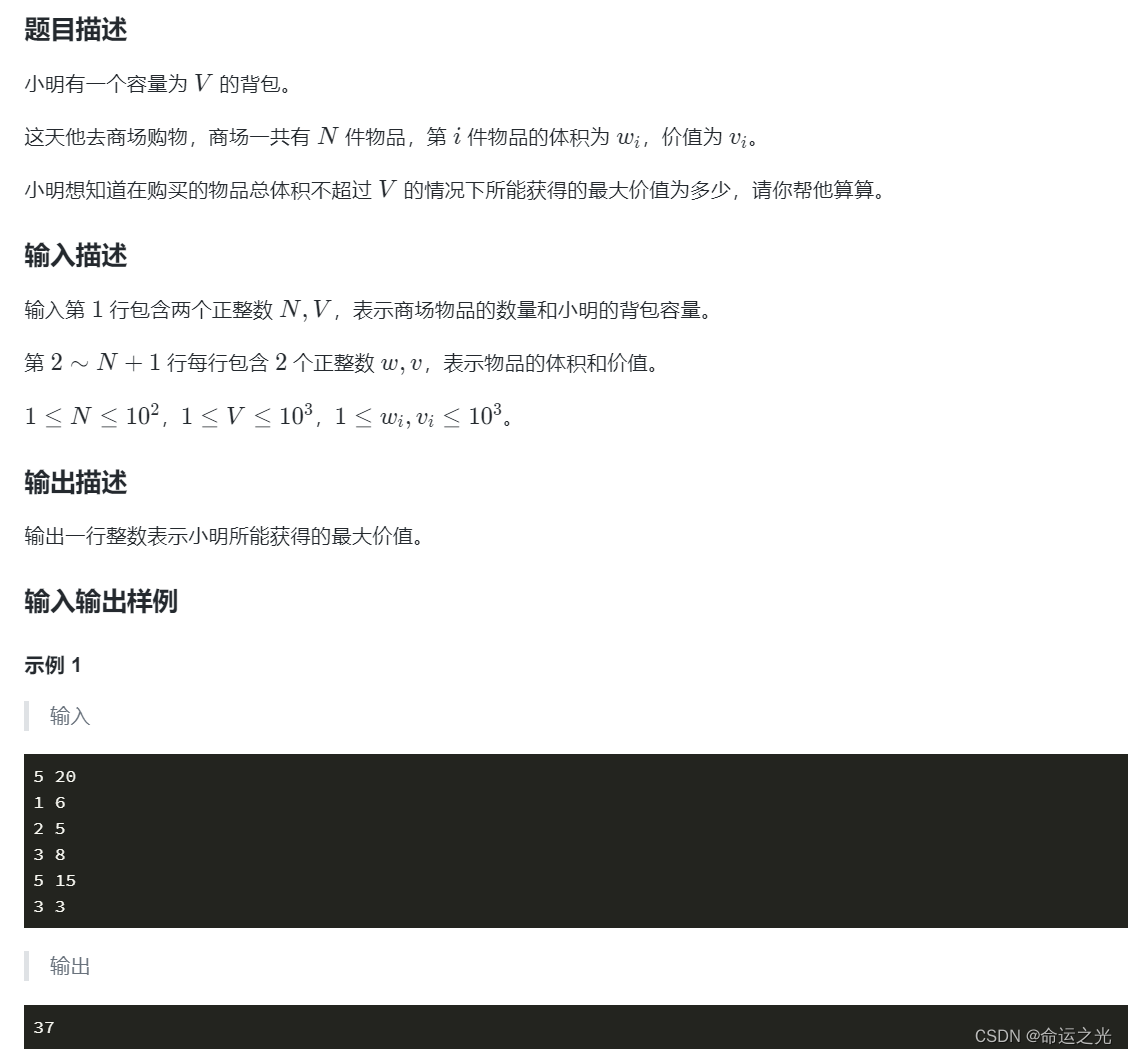
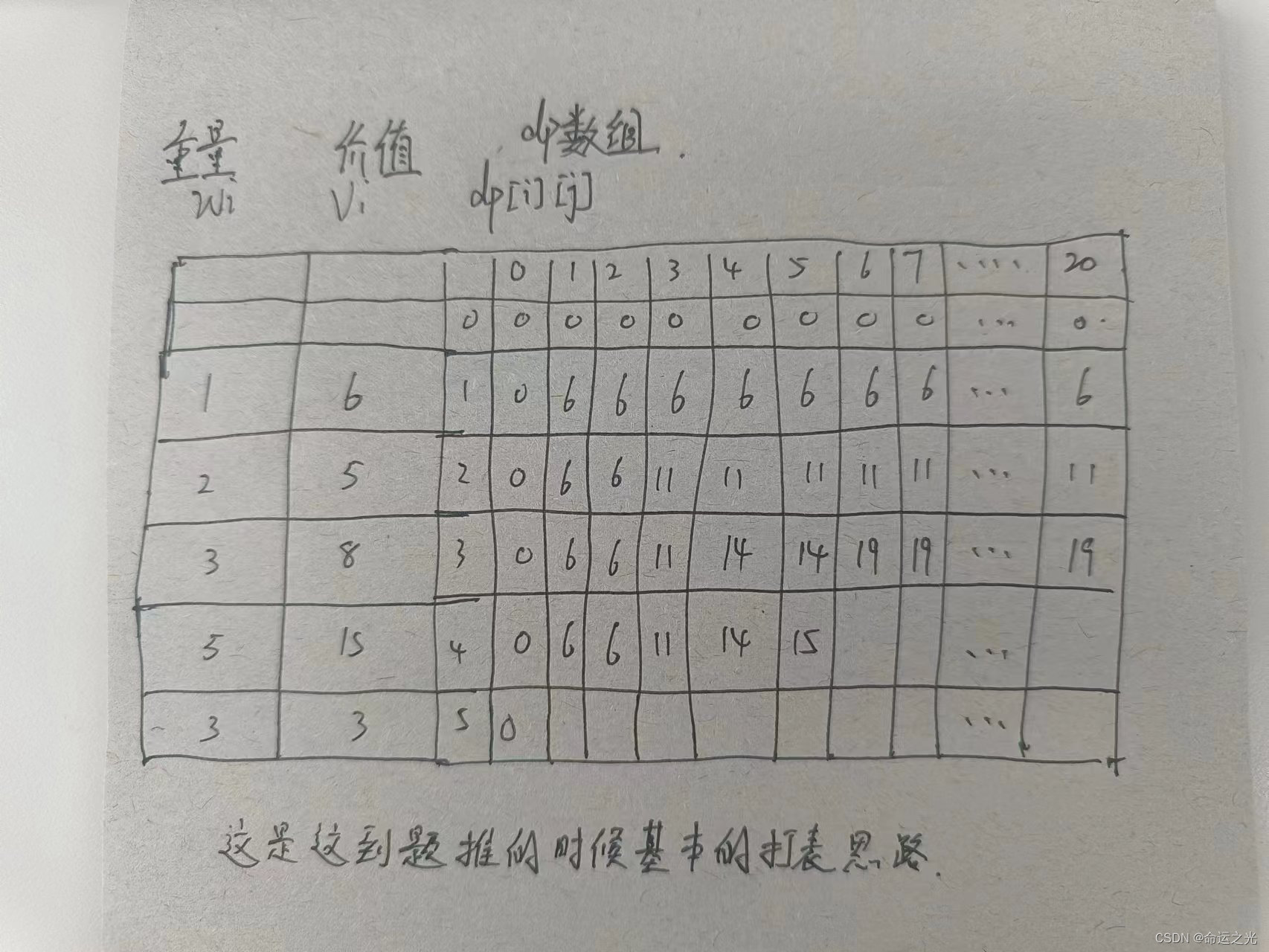
🍓解题代码

#include<bits/stdc++.h>
using namespace std;
int wi[105],vi[105],dp[1005][1005];
int main()
{int n,v;//n为行数，v为背包的大小cin>>n>>v;//传入n，v的值for(int i=1;i<=n;i++){cin>>wi[i]>>vi[i];//传入重量和价值 }//写dp数组int i,j;for(i=1;i<=n;i++){for(j=1;j<=v;j++){if(j<wi[i]){dp[i][j]=dp[i-1][j];//如果重量没j大的话，就直接继承dp数组上一列的最优解，直接dp[i-1][j]即可 }else{//若是比j大则进行比较，这道题标准的01背包问题，直接套用01背包推出的公式即可 dp[i][j]=max(dp[i-1][j],dp[i-1][j-wi[i]]+vi[i]);	} }} cout<<dp[n][v];return 0;
}

🍓dp数组打表如下：

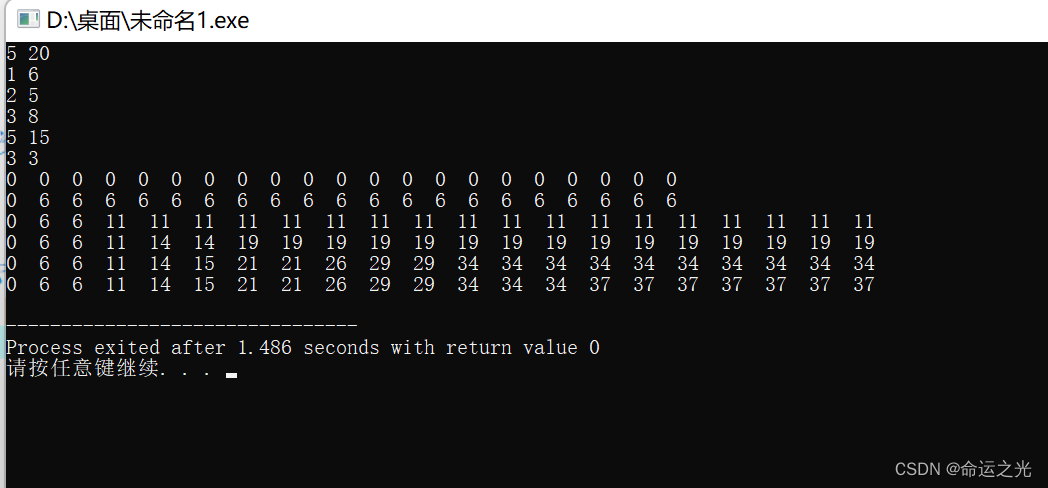✨经典01背包问题的解题思路

在C/C++中，可以使用动态规划来解决01背包问题。动态规划是一种常用的解决优化问题的算法思想，它通过将问题分解为子问题，并利用子问题的解来构建更大规模的问题的解。

以下是使用动态规划解决01背包问题的基本步骤：

定义问题：我们需要确定背包的容量和物品的重量和价值。假设背包的容量为C，有n个物品，每个物品的重量为w[i]，价值为v[i]。
创建一个二维数组dp[n+1][C+1]，其中dp[i][j]表示在前i个物品中，背包容量为j时的最大价值。
初始化边界条件：当物品数量为0或背包容量为0时，最大价值都为0，即dp[i][0] = dp[0][j] = 0。
递推关系：对于每个物品i，我们有两种选择：放入背包或不放入背包。如果选择放入背包，那么当前的最大价值为dp[i][j] = dp[i-1][j-w[i]] + v[i]；如果选择不放入背包，那么当前的最大价值为dp[i][j] = dp[i-1][j]。我们选择两者中的较大值作为dp[i][j]的值。
递推计算：使用循环遍历物品和背包容量，根据递推关系计算dp[i][j]的值。
返回结果：dp[n][C]即为问题的解，表示在前n个物品中，背包容量为C时的最大价值。

🍓下面是一个示例代码，演示了如何使用动态规划解决01背包问题：

#include <iostream>
using namespace std;int knapsack(int C, int weights[], int values[], int n) {int dp[n + 1][C + 1];// 初始化边界条件for (int i = 0; i <= n; i++)dp[i][0] = 0;for (int j = 0; j <= C; j++)dp[0][j] = 0;// 计算最大价值for (int i = 1; i <= n; i++) {for (int j = 1; j <= C; j++) {if (weights[i - 1] <= j) {dp[i][j] = max(values[i - 1] + dp[i - 1][j - weights[i - 1]], dp[i - 1][j]);} else {dp[i][j] = dp[i - 1][j];}}}return dp[n][C];
}int main() {int C = 10;  // 背包容量int weights[] = {2, 3, 4, 5};  // 物品重量int values[] = {3, 4, 5, 6};   // 物品价值int n = sizeof(weights) / sizeof(weights[0]);  // 物品数量int max_value = knapsack(C, weights, values, n);cout << "最大价值：" << max_value << endl;return 0;
}

在这个示例中，背包的容量C为10，有4个物品，重量分别为2、3、4和5，价值分别为3、4、5和6。运行程序将输出最大价值为10，即当背包容量为10时，从这些物品中选择可以得到的最大价值。你可以根据实际情况修改输入的背包容量、物品重量和价值，来解决不同的01背包问题。

✨01背包的递推公式（重要需要记忆）

dp[i][j] = max(dp[i-1][j], dp[i-1][j-w[i]] + v[i])

其中，dp[i][j]表示在前i个物品中，背包容量为j时的最大价值，w[i]表示第i个物品的重量，v[i]表示第i个物品的价值。

递推公式的含义是，在考虑第i个物品时，我们有两种选择：

不选择第i个物品，即仅考虑前i-1个物品，此时的最大价值为dp[i-1][j]。
选择第i个物品，那么背包的容量就会减少，变为j-w[i]，此时的最大价值为dp[i-1][j-w[i]] + v[i]，即在考虑前i-1个物品、背包容量为j-w[i]时的最大价值，再加上第i个物品的价值v[i]。

我们选择上述两种选择中的较大值作为dp[i][j]的值，即表示在考虑前i个物品、背包容量为j时的最大价值。

需要注意的是，上述递推公式中的dp数组是一个二维数组，大小为(n+1) x (C+1)，其中n表示物品的数量，C表示背包的容量。初始化时，需要设置边界条件，即dp[0][j] = dp[i][0] = 0，表示当物品数量为0或背包容量为0时的最大价值为0。