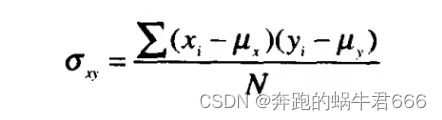一.表格法和图形法
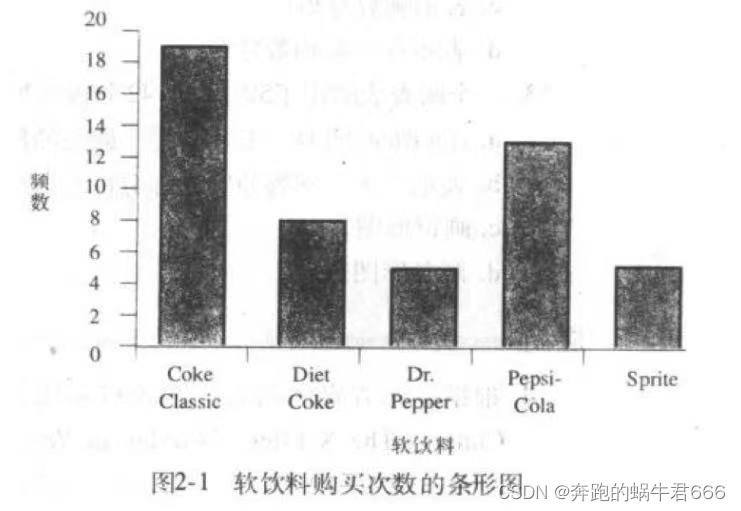
条形图
是一种描述已在一个频数,相对频数或百分数频数分布中汇总的品质数据的图形方法
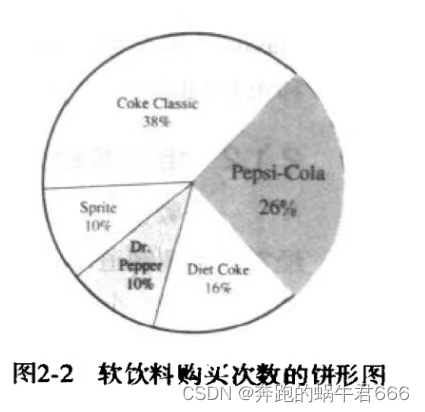
饼形图
是一种常用的描绘品质数据的相对频数分布的图形方法
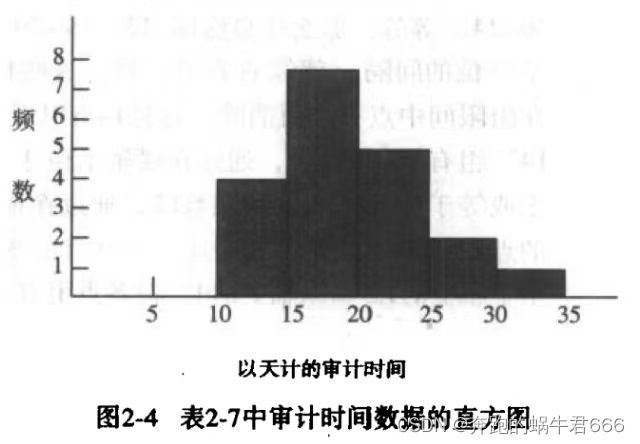
直方图
横轴上表示所关心的变量,纵轴上表示频数,相对频数或百分数频数
探索性数据分析:茎叶显示

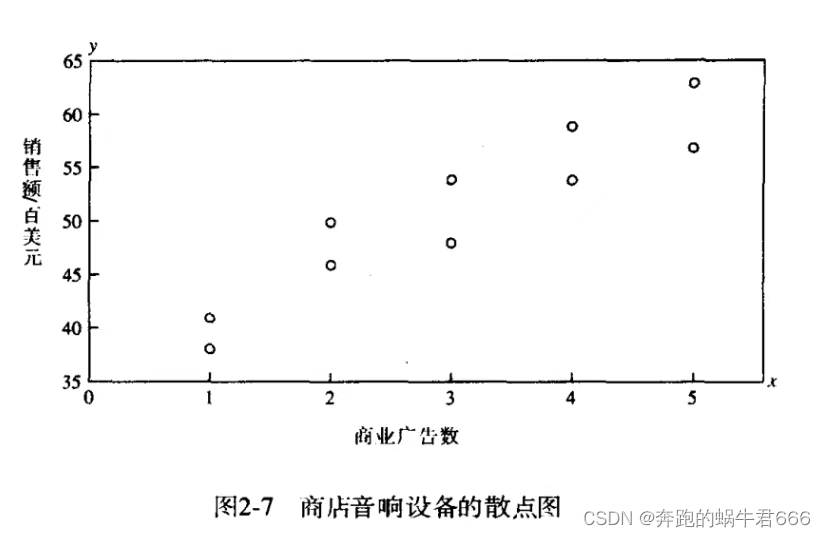
散点图
两个数量变量间的关系的图形表示
二.数值方法
1.位置的度量
平均数
用以衡量某个数据集的中心位置
将所有数据的值加总,再除以数据的项数,就得到了平均数
中位数
是另一个反映数据的中心位置的量度
将所有数据项以递增顺序排列,位于中央的数据的值就是中位数。如果项数为奇数,则中位数就是位于中央的那一项数值;如果项数为偶数,中央两项数值的平均值就是中位数
众数
指在数据中发生频数最高的数据值
百分位数
是用于衡量数据的位置的量度,但它所衡量的,不一定是中心位置
百分位数提供了有关数据项如何在最小值和最大值之间分布的信息
四分位数
将数据划分为4个部分,这种划分的临界点就是四分位数
第1四分位数:第25百分位数
第2四分位数:第50百分位数
第3四分位数:第75百分位数
2.变异程度的度量
全距
= 最大值 - 最小值
四分位数间距
= 第1四分位数 - 第3四分位数
方差
利用所有数据的值计算而来的衡量变异程度的量度
①总体方差:数据集是整体,离差的平方的平均值
②样本方差:样本关于平均数的离差的平方除以(n-1),而不是n,得到的样本方差是对于总体方差的无偏估计
标准差
方差的正的平方根
标准差和原来的数据有着相同的单位衡量,鉴于这个原因,标准差更容易与平均数以及其他与原始数据单位相同的统计量进行比较
3.相对位置的度量和异常值检测
Z分数
利用平均数和标准差,我们可以知道任何数据值的相对位置

切比雪夫定理
使我们能够估计与平均数的距离在特定数目个标准差范围之内的项占总项数的百分比
内容:在任意一个数据集中,至少有(1-a/z^2)的数据项与平均数的距离在z个标准差之内,其中z是任意大于1的值
对于钟型分布的数据:约68%的数据项与平均数的距离在1个标准差之内
约95%的数据项与平均数的距离在2个标准差之内
几乎所有的数据项与平均数的距离在3个标准差之内
4.探索性数据分析
五数概括法
即用五个数来概括数据
①最小值
②第1四分位数(Q1)
③中位数(Q2)
④第3四分位数(Q3)
⑤最大值
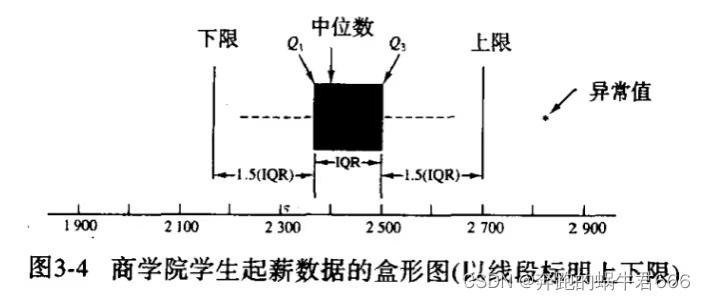
盒型图
画法步骤
①画一个方盒,其边界恰好是第1和第3四分位数
②在方盒上中位数的位置画一条垂线,因此中位数将数据分为相等的两个部分
③利用四分位数间距IQR = Q3 - Q1来设定界限
④须线从方盒的边线出发,直至上下限之内的最大值和最小值
⑤任一异常值的位置以符号“ * ”标出
 5.两变量间关系的度量
5.两变量间关系的度量
协方差
①样本协方差
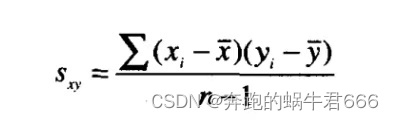
②总体协方差