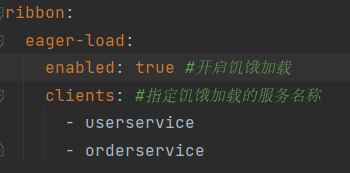
一.联合查询
面试问题:
聚合查询与联合查询的区别
聚合查询是行与行之间的数据加工
聚合函数 :count,sum,avg...
group by 进行分组,指定列的值,相同的记录合并到同一个组,每个组又可以分别进行聚合查询
分组还可以指定条件筛选,如果分组之前指定条件 用where,如果对分组之后指定条件,用having

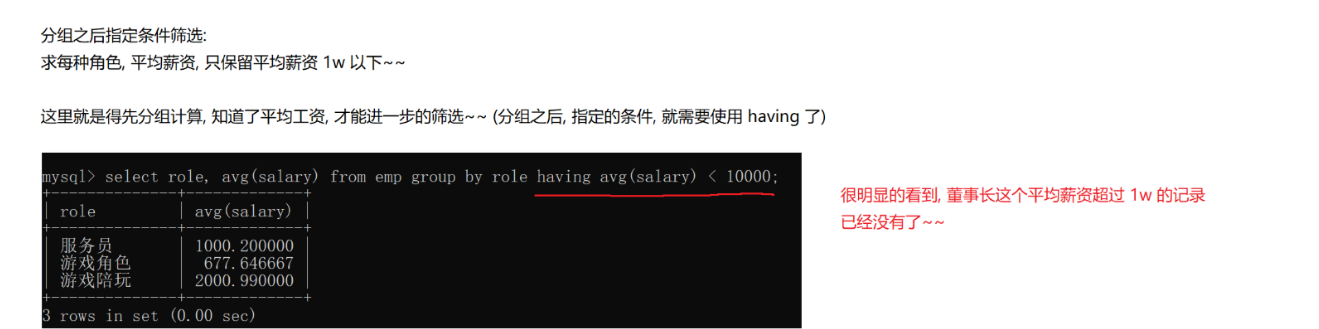
联合查询(多表查询) 关键操作就是笛卡尔积
1.自连接
自己和自己进行笛卡尔积,自连接的本质其实是把行与行之间的比较条件转换成列和列


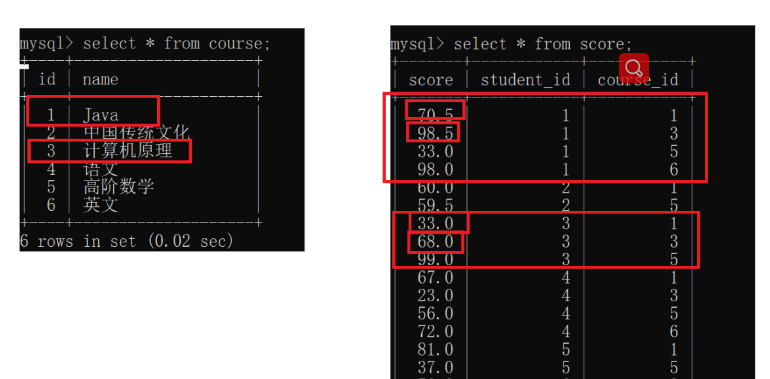


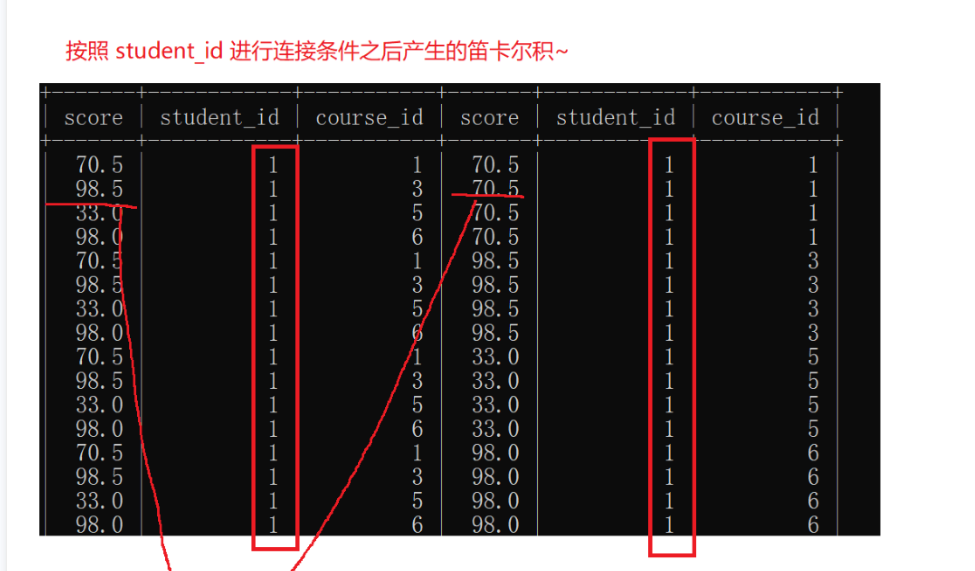



自连接的关键就是可以把行转换成列
2.子查询
本质就是套娃,子查询就是把拆分好的代码合并再一起
子查询是指嵌入在其他sql语句中的select语句,也叫嵌套查询
单行子查询:返回一行记录的子查询
查询与“不想毕业” 同学的同班同学:

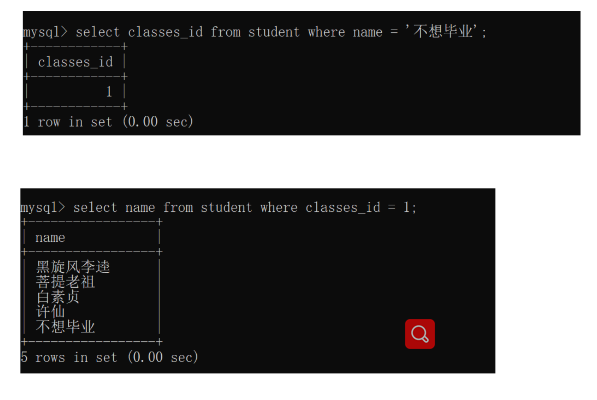
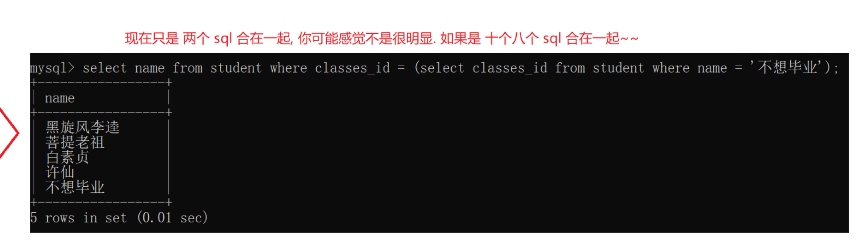
有时候子查询可能会查询出多条记录,就不能用= 就要用in这样的操作
多行子查询
返回多行记录的子查询
案例:查询“语文”或“英文”课程的成绩信息

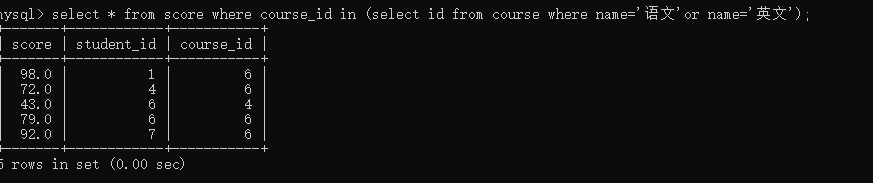
3.合并查询
多个查询结果合并到一起,为了合并多个select的执行结果,可以使用集合操作符 union,union all。使用UNION
和UNION ALL时,前后查询的结果集中,字段需要一致。


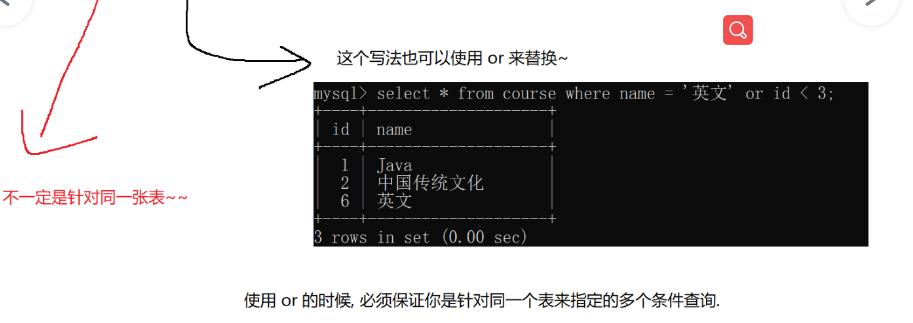
union操作会自动的进行去重,union是不会去重的,
二.MySQL的索引事务(面试)
1.索引
1.1概念
索引是一种特殊的文件,包含对数据表里所有记录的引用指针.可以对表中的一列或者多列创建索引,并指定索引的类型,各类索引有各自的数据结构实现,


1.2作用
索引的主要意义就是查找,提高查找的效率, 但是付出了代价, 书的目录是废纸,数据库的索引需要消耗一定的额外的存储空间,
数据量越大,索引消耗的额外空间就越多,书的目录如果确定了,后续对书的内容调整,都可能会影响到目录的准确性,就需要调整目录 ,数据库的额索引也是一样,当进行增删查改的时候,往往需要同步调整索引的结构,
优点:提高查找速度,缺点:占用了更多空间,并拖慢了增删改的速度

1.3 使用场景
要考虑对数据库表的某列或某几列创建索引,需要考虑以下几点:
数据量较大,且经常对这些列进行条件查询。
该数据库表的插入操作,及对这些列的修改操作频率较低。
索引会占用额外的磁盘空间。
满足以上条件时,考虑对表中的这些字段创建索引,以提高查询效率。
反之,如果非条件查询列,或经常做插入、修改操作,或磁盘空间不足时,不考虑创建索引。
1.4使用
查看索引



创建索引


删除索引

1.5索引背后的数据结构(面试)
面试中考察重点是索引背后的数据结构
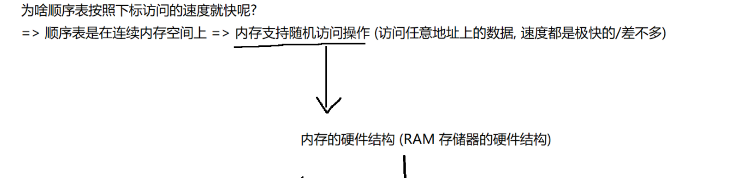
1.如果是顺序表和链表,想要查找,就需要遍历
这里的查找是按照"数值查找"
并不是按照"下标查找",按照下标来访问元素,不叫查找

2.二叉搜索树
查找的时间复杂度是o(N)
最坏的情况下,是单分支的树,就是链表
AVL:要求任意节点左右子树高度差不超过1
红黑树 :要求更宽松的平衡二叉树
二树的最大的问题:当元素多了时候,高度就高了(高度对应着比较次数),对于数据库来说,每次比较都代表磁盘io
3.哈希表
虽然哈希表查找速度很快(o(1))
但是哈希表只能针对"相等"进行判定,不能对"大于小于:",以及范围查找
4.堆
只能找最大最小
最适合做索引还是树形结构,只不过不再是二叉树
使用"多叉搜索树",高度自然就下降
5.B+树
数据库索引中最常见的数据结构:B+树

如果想要了解B+树,要先了解它的前身,B树 有些资料也叫B-树

原理:B树的每个节点上,都会存储N个key值
N个key值都划分除了N+1个区间,每个区间都对应一个子树
数据:10,12,15,16,17,20,21,22,25,30,33,35,37,40,41,48,50,55,60,70,90
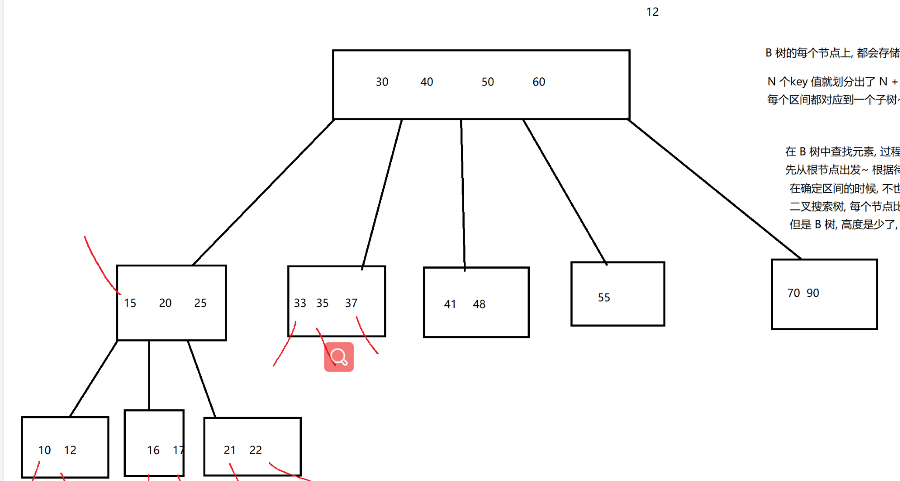
在B树中查找元素,过程就和二叉搜索树相似
先从根节点出发,根据待比较的元素,确定一个区间.
在确定区间的时候进行多次比较
这里和二叉搜索树的区别在哪里
二叉树 每个节点比一次,比较的次数与高度有关
但是B树 高度少了,但是每个节点比较多次

数据 1,2,3,5,6,8,9,11,13,15
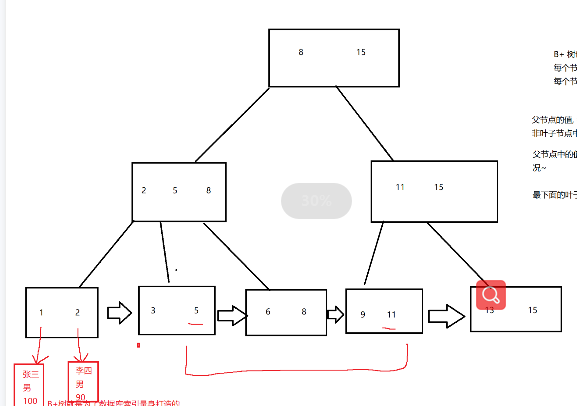
B+树也是一个N叉搜索树
每个节点都包含多个key值
每个节点如果有N个key,就分成了N个区间
父节点的值都会在子节点中体现
非叶子节点的每个值,都会在叶子节点体现出来
父节点的值,都会作为子节点的最大值(最小值),这个图画的是最大值的情况
最下面的叶子节点,就使用链表进行顺序连接
B+树的优点
为数据库索引量身打造
1.使用B+树进行查找,整体的IO次数会降低
2.所有的查询最终会落到叶子节点上,每次查询的IO次数都是差不多,查询速度是稳定的
3.叶子结点用链表连接后,非常适合范围查找
4.所有的数据存储(载荷)都是放在叶子结点上,非叶子节点存储的是key值,因此非叶子结点整体占用空间小,甚至可以缓存到内存中,一旦全放在努力存,那么磁盘IO都没了


2.事务
将若干个独立的操作打包成一个整体


2.1原子性
要么全都执行完,要么一个都不执行,任务不可再被细分
举例



事务的原子性,能避免出现这种中间状态


这种还原性工作叫回滚(rollback)

数据库是如何直到还原成哪个值呢


2.2.事务四个特性(面试)
1.原子性
2.一致性
在事务执行之前,和执行之后,数据库中的数据都得是合理合法的,
例如:转账以后不能出现账户为负数的额情况
3.持久性
事务一旦移交,数据就持久化存储起来----写入到硬盘中
4.隔离性(重点)
描述的是,事务并发执行的时候,产生的情况

举例:


最后我把代码改了
1.脏读问题:


解决方法:给写操作加锁


2.不可重复读问题





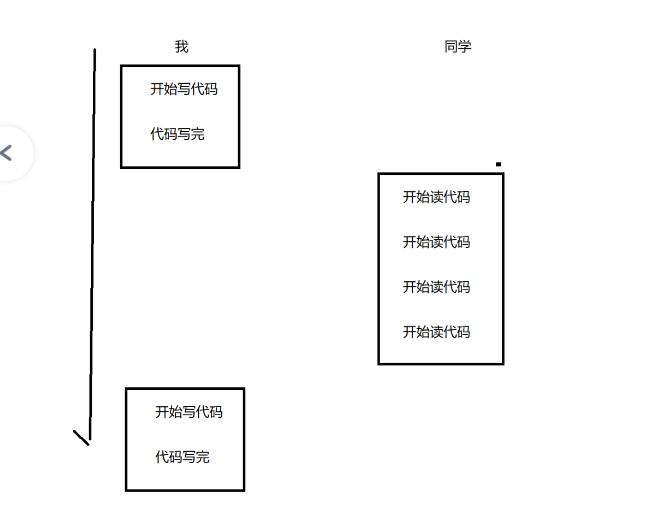
3.幻读问题
一个事务执行过程中进行多次查询,多次查询的结果不一样(多了一条或者少了一条) 这种也算是一种特殊的不可重复读

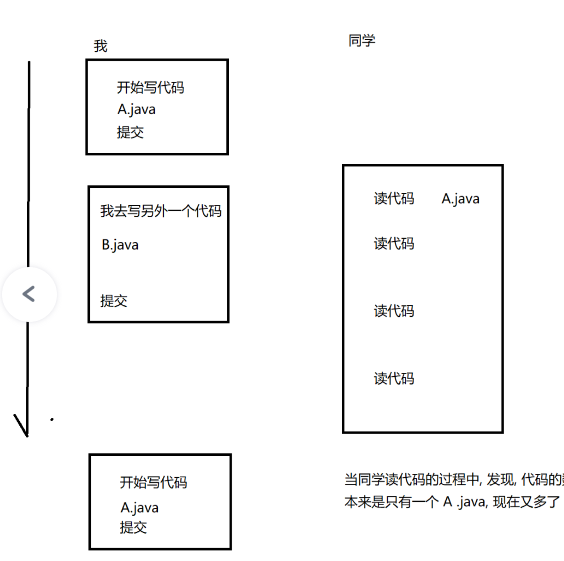

解决方法:彻底串行化执行