在学习这些内容之前,需要学习python数据分析相关内容:
numpy:科学计算库,处理多维数组,进行数据分析
pandas:基于numpy的一种工具,该工具是为了解决数据分析任务而创建的
matplotlib:python的2D绘图库
matplotlib.plot:提供一个类似matlab的绘图框架
见上一篇:python数据分析学习笔记之matplotlib、numpy、pandas,鄙人较菜,望多多指教,共同进步
以下代码有的加注释,主要是学习过程中为了查看数据,需要的可以去掉注释,怎样都行,自己DIY
1.单变量线性回归
案例:假设你是一家餐厅的CEO,正在考虑开一家分店,根据该城市的人口数据预测其利润。拥有不同城市对应的人口数据以及利润:exercise1.py和ex1data1.txt
梯度下降实现线性回归,以最小化成本函数。
创建一个以参数θ为特征函数的代价函数
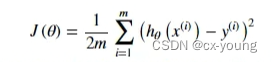
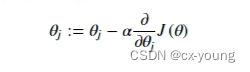
以下代码为了清晰,分步骤展示的,对应名称exercise1.py为完整顺序代码,数据为ex1data1.txt
导入所需库
# 导入需要使用的包
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
代价函数(损失函数) 误差
# 代价函数(损失函数) 误差
def computerCost(X, y, theta):# inner 每个元素都作了平方的列矩阵inner = np.power(((X * theta.T) - y), 2)return np.sum(inner) / (2 * len(X))
批量梯度下降函数
'''
X:输入
y:输出
alpha:学习率
iters:迭代次数
'''
def gradientDescent(X, y, theta, alpha, iters):# 构建等值矩阵 大小和theta一样(1,2) 存放参数theta[0],theta[1]temp = np.matrix(np.zeros(theta.shape))# 参数的个数 此处为2# ravel()计算需要求解的参数个数,功能将多维数组降至一维parameters = int(theta.ravel().shape[1])# 矩阵 保存每一次迭代后的costcost = np.zeros(iters)for i in range(iters): # 迭代次数error = (X * theta.T) - yfor j in range(parameters):# multiply 逐点相乘 每个元素对应乘起来term = np.multiply(error, X[:, j])temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))theta = temp # 更新的参数放到thetacost[i] = computerCost(X, y, theta)return theta, cost
读取数据并展示
# data.txt与本文件放在同一个文件夹下
data = pd.read_csv("ex1data1.txt", header=None, names=['Population', 'Profit'])
# 数据可视化,绘制散点图kind,取值为line或scatter figsize设置大小
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12, 8))
# plt.show()#展示时去掉注释
原始数据所展示的散点图
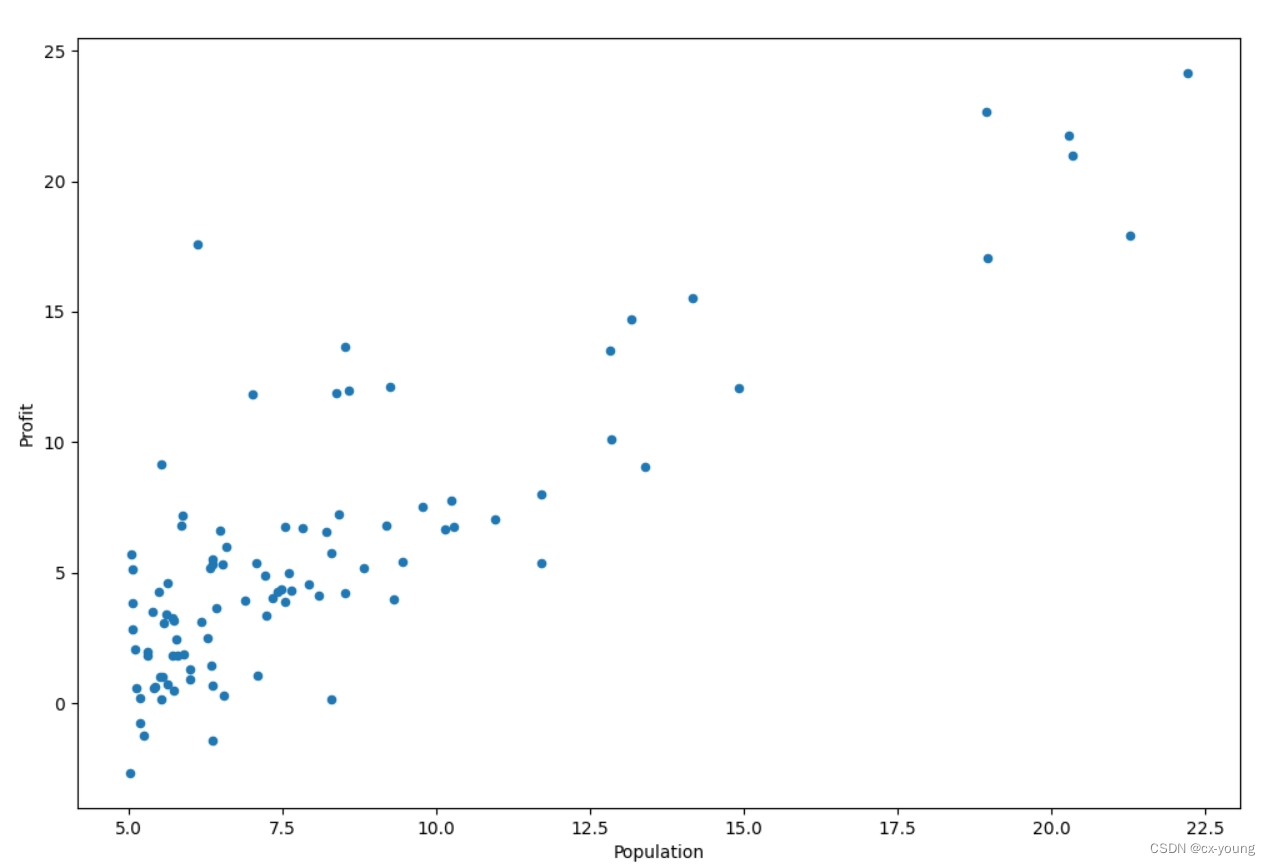
在训练集中添加一列
# 在训练集中添加一列,以便可以使用向量化的解决方案计算代价和梯度
# 在训练集的左侧插入一列全为1的列
# 以便计算即x0=1 loc为0,name为ones,value为1
data.insert(0, 'ones', 1)
print(data)#查看数据
输出结果:
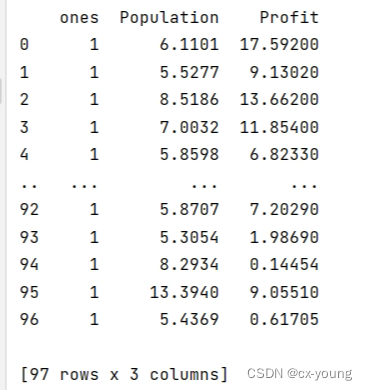
分割行与列,得到需要的矩阵
# shape[1]代表列
cols = data.shape[1]
# print(cols)#3
# iloc是左闭右开
X = data.iloc[:, 0:cols - 1] # X是所有行,去掉最后一列
y = data.iloc[:, cols - 1:cols] # y是所有行,只要最后一列
# print(X) #查看X
# print(y)#查看y
# plt.show()
# 代价函数是numpy矩阵,需要转换X和y为矩阵,然后才能使用它们。
# 还需要初始化theta,即把theta的所有元素都设置为0
X = np.matrix(X.values)
y = np.matrix(y.values)
# theta是一个(1,2)矩阵 theta初始值为0
theta = np.matrix(np.array([0, 0]))
# 分别查看X、y,theta的维度
# print(X.shape,y.shape,theta.shape)#(97, 2) (97, 1) (1, 2)
# 计算代价函数 theta初始值为0
costs = computerCost(X, y, theta)
print('计算代价函数 theta初始值为0:', costs)
计算代价函数 theta初始值为0: 32.072733877455676
初始化一些变量
# 初始化一些附加变量,学习率和要执行的迭代次数
alpha = 0.01#学习率
iters = 1000#迭代次数
运用梯度下降函数将参数theta应用于训练集
g, cost = gradientDescent(X, y, theta, alpha, iters)
print(g)
使用拟合的参数计算训练模型的代价函数(误差)
costs = computerCost(X, y, g)
print('使用拟合的参数计算训练模型的代价函数(误差):', costs)
绘图之拟合函数
# 绘制线性模型以及数据,直观看出它的拟合,fig代表整个图像,ax代表实例
x = np.linspace(data.Population.min(), data.Population.max(), 100) # 抽100个样本
f = g[0, 0] + (g[0, 1] * x) # g[0,0]代表theta0,g[0,1]代表theta1fig, ax = plt.subplots(figsize=(12, 8))
# 绘制折线图
ax.plot(x, f, 'r', label="Prediction")
# 绘制散点图
ax.scatter(data.Population, data.Profit, label='Training data')
ax.legend(loc=4)#显示标签位置
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
结果展示:
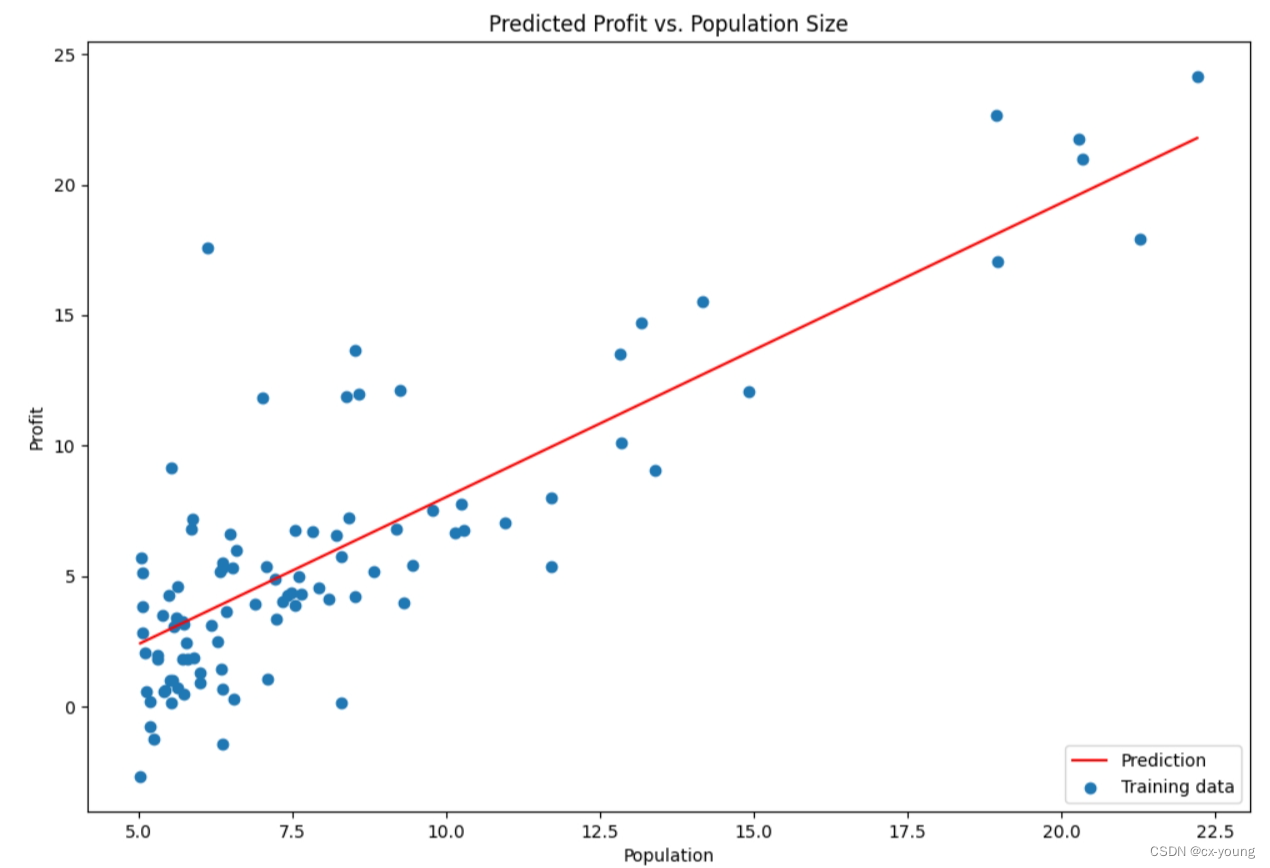
绘图之梯度下降图展示
#由于梯度方程式函数在每个训练迭代中输出一个代价的向量,也可以绘制
fig, ax1 = plt.subplots(figsize=(12, 8))
ax1.plot(np.arange(iters),cost,'r')
ax1.set_xlabel('Iterations')
ax1.set_ylabel('Cost')
ax1.set_title('Error vs. Training Epoch')
plt.show()
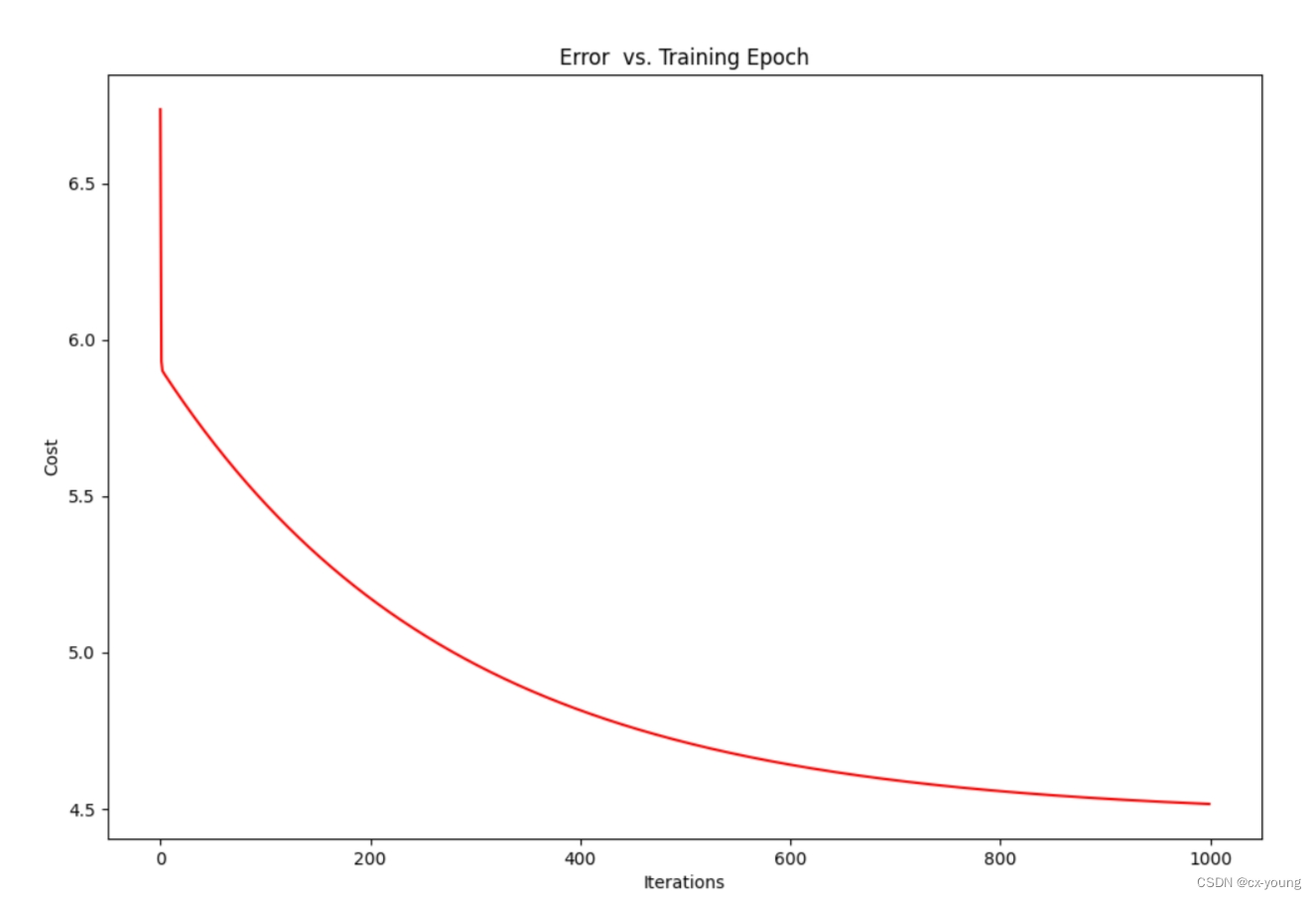
多变量线性回归
案例:假设你现在打算卖房子,想知道房子多少钱
我们拥有房子面积和卧室数量以及房子价格之间的对应数据:exercise1_plus.py和ex1data2.txt
导入所需库
# 导入需要使用的包
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
代价函数(损失函数) 误差
# 代价函数(损失函数) 误差
def computerCost(X, y, theta):# inner 每个元素都作了平方的列矩阵inner = np.power(((X * theta.T) - y), 2)return np.sum(inner) / (2 * len(X))
批量梯度下降函数
'''
X:输入
y:输出
alpha:学习率
iters:迭代次数
'''
def gradientDescent(X, y, theta, alpha, iters):# 构建等值矩阵 大小和theta一样(1,2) 存放参数theta[0],theta[1]temp = np.matrix(np.zeros(theta.shape))# 参数的个数 此处为2# ravel()计算需要求解的参数个数,功能将多维数组降至一维parameters = int(theta.ravel().shape[1])# 矩阵 保存每一次迭代后的costcost = np.zeros(iters)for i in range(iters): # 迭代次数error = (X * theta.T) - yfor j in range(parameters):# multiply 逐点相乘 每个元素对应乘起来term = np.multiply(error, X[:, j])temp[0, j] = theta[0, j] - ((alpha / len(X)) * np.sum(term))theta = temp # 更新的参数放到thetacost[i] = computerCost(X, y, theta)return theta, cost
读取数据并展示
#读取数据
data2 = pd.read_csv('ex1data2.txt', header=None, names=['Size', 'Bedrooms', 'Price'])
# print(data2)#查看数据
数据预处理:特征归一化
消除特征值之间的量纲影响,个特征值处于同一数量级
提升模型的收敛速度与精度
'''
预处理步骤:特征归一化
对于此任务,添加一个预处理步骤,特征归一化
若房子价格不归一化,它的数量级和输入值归一化数量级差别太大
几十万的数量级和个位小数做回归
就不能保证收敛了预测的y和实际y几十万差的太多了
'''
# 每个数据 = (每个数据 - 均值)➗方差
data2 = (data2 - data2.mean()) / data2.std()
在训练集中添加一列
# 添加全为1的一列
data2.insert(0, 'ones', 1)
分割行与列,得到需要的矩阵
# shape[1]代表列
cols = data2.shape[1]
X2 = data2.iloc[:, 0:cols - 1] # X2是所有行,去掉最后一列,即保留前三列
y2 = data2.iloc[:, cols - 1:cols] # y2是所有行,只要最后一列 列矩阵
# 代价函数是numpy矩阵,需要转换X2和y2为矩阵,然后才能使用它们。
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
# 还需要初始化theta,即把theta的所有元素都设置为0
theta2 = np.matrix(np.array([0, 0, 0]))
初始化一些变量
#不同alpha(学习率)下的效果
alphas = [0.0003,0.003,0.03,0.0001,0.001,0.01]
# 要执行的迭代次数
iters = 2000
绘图
# 开始绘图
fig, ax = plt.subplots()
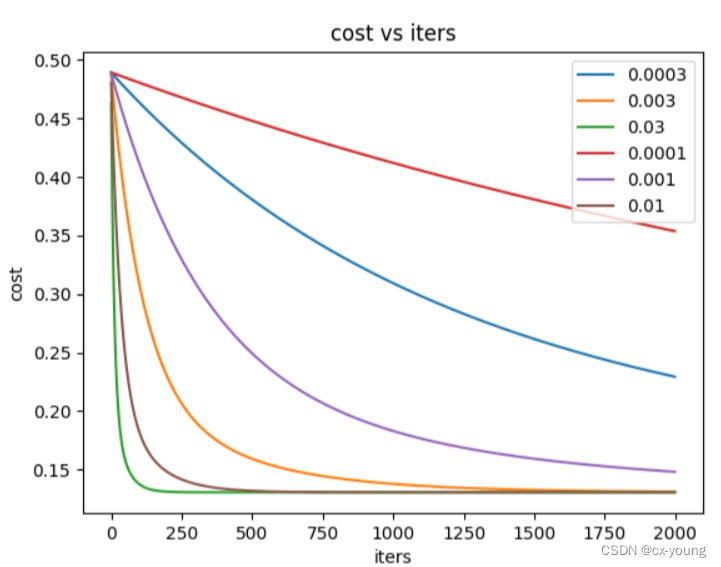
for alpha in alphas:_, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)ax.plot(np.arange(iters), cost2, label=alpha)ax.legend()ax.set(xlabel='iters', ylabel='cost', title='cost vs iters')
# 由于梯度方程式函数在每个训练迭代中输出一个代价的向量,也可以绘制
fig, ax1 = plt.subplots(figsize=(12, 8))
ax1.plot(np.arange(iters), cost2, 'r')
ax1.set_xlabel('Iterations')
ax1.set_ylabel('Cost')
ax1.set_title('Error vs. Training Epoch')
plt.show()
迭代过程中代价的变化
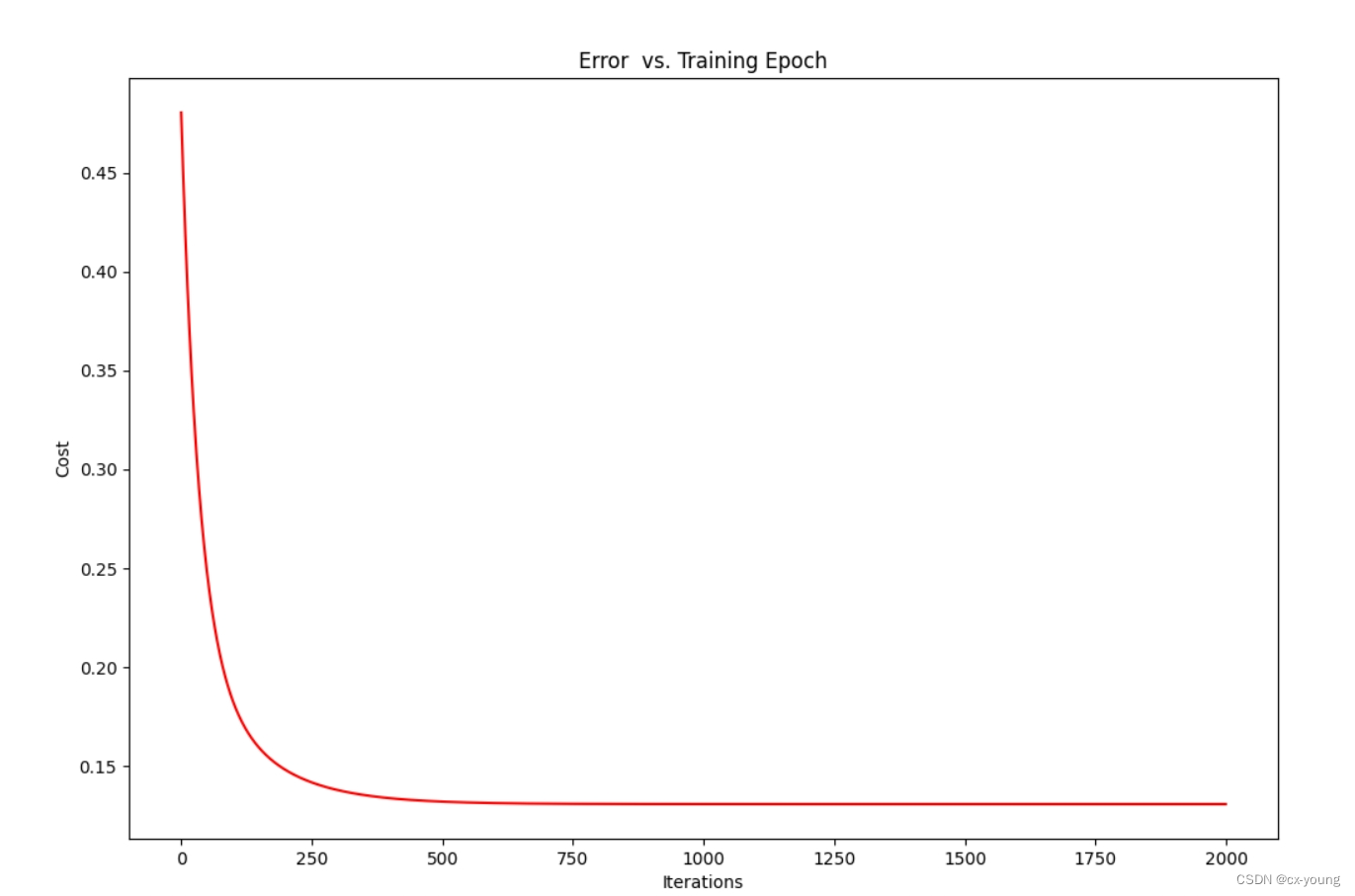
不同alpha(学习率)下的效果
正规方程
对应于Zhenggui.py
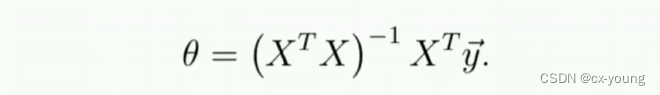
若不可逆了,一般要考虑以下两者情况
- 移除冗余特征。一些特征存在线性依赖
- 特征太多,要删除一些特征。比如(m<n),对于小样本数据使用正则化
numpy.linalg模块包含线性代数的函数。使用这个模块,可以计算逆矩阵、求特征值、解方程组及求解行列式等
inv函数计算逆矩阵
# 导入需要使用的包
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd# data.txt与本文件放在同一个文件夹下
data = pd.read_csv("ex1data1.txt", header=None, names=['Population', 'Profit'])
# 数据可视化,绘制散点图kind,取值为line或scatter figsize设置大小
data.plot(kind='scatter', x='Population', y='Profit', figsize=(12, 8))
# plt.show()# 在训练集中添加一列,以便可以使用向量化的解决方案计算代价和梯度
# 在训练集的左侧插入一列全为1的列
# 以便计算即x0=1 loc为0,name为ones,value为1
data.insert(0, 'ones', 1)
# print(data)#查看数据
# shape[1]代表列
cols = data.shape[1]
# print(cols)#3
# iloc是左闭右开
X = data.iloc[:, 0:cols - 1] # X是所有行,去掉最后一列
y = data.iloc[:, cols - 1:cols] # y是所有行,只要最后一列
# print(X) #查看X
# print(y)#查看y
# plt.show()
# 代价函数是numpy矩阵,需要转换X和y为矩阵,然后才能使用它们。
# 还需要初始化theta,即把theta的所有元素都设置为0
X = np.matrix(X.values)
y = np.matrix(y.values)# 正规方程
def normalEquation(X, y):theta = np.linalg.inv(X.T @ X) @ X.T @ yreturn thetatheta = normalEquation(X, y)
print(theta)
绘图
# 绘制线性模型以及数据,直观看出它的拟合,fig代表整个图像,ax代表实例
x = np.linspace(data.Population.min(), data.Population.max(), 100) # 抽100个样本
f = theta[0, 0] + (theta[1, 0] * x) # theta[0,0]代表theta0,theta[0,1]代表theta1
# print(x)
# print(theta[0, 0])
# print(f)
# print(x.shape)
# print(f.shape)fig, ax = plt.subplots(figsize=(12, 8))
# 绘制折线图
ax.plot(x, f, 'r', label="Prediction")
# 绘制散点图
ax.scatter(data.Population, data.Profit, label='Training data')
ax.legend(loc=4)#显示标签位置
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
感谢B站上的up主
https://www.bilibili.com/video/BV1Xt411s7KY?p=1&vd_source=b3d1b016bccb61f5e11858b0407cc54e
https://www.bilibili.com/video/BV124411A75S/?spm_id_from=333.1007.top_right_bar_window_history.content.click&vd_source=b3d1b016bccb61f5e11858b0407cc54e