离散数学复习纲要

• 图

1. 欧拉图：无向图的话，需要是连通图，所有结点需要是偶度数。
2. 哈密顿通路：经过图中各个顶点一次且仅一次的通路，任意两顶点度数之和大于等于n-1
3. 哈密顿回路：经过图中各个顶点一次且仅一次的回路，任意两顶点度数之和大于等于n，第一个顶点和最后一个顶点要相同
4. 树的边数 = 顶点数 – 1（生成树）
5. 平凡树：只有一个顶点没有树叶
6. 非平凡树：至少有两片树叶
7. 树：无回路 / 连通 且 m = n – 1
8. 任何无向图中，度数和 = 边数 * 2
9. 只有偶数个奇度数的顶点集合才能构成图
10. 无向图有生成树：连通图
11. 权值：不包括叶子节点
12. 最佳前缀码：最优二叉树生成的前缀码（左0右1）
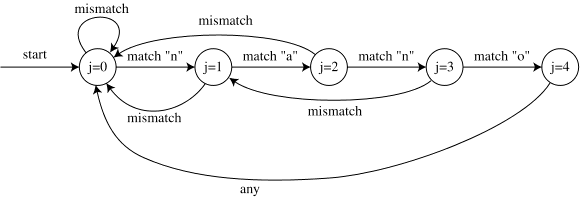
13. 判断能否构成前缀码：从两位（n）的看起，如果前n-1位在之前出现过，那构不成前缀码
14. 无向图：每一条边都无向边、且无自回路的图
15. 简单无向图中至少有两个顶点次数相同

• 偏序

1. 上界、下界是在全局范围内找到≥（≤）的元素

1. 上下界的元素可以是自己集合内的点的情况只能是这个点处于整个集合的最底（顶）端，其余的情况只能是高（低）于，不能等于的外界点
2. 等于的情况（且只能是）：自己内部可比较的最大（小）点

1. 最大元最小元是在整个集合中找，极大极小也是

• 集合

1. 环和：a 环和 b = (a - b) ∪ (b - a)
2. 不是带了大括号就是集合，如果集合中有子集合，那么这个子集合也可以是元素
3. N个元素的集合有2^(n^2)个二元关系（每个元素可以选择出现和不出现两种情况），有2^n个一元关系
4. 两个集合做笛卡尔积，元素个数为两个集合元素个数之积
5. 等价是蕴含式相析取
6. 划分诱导的等价关系是各个元素的笛卡尔积

• 二元关系

1. 等价关系：自反、传递、对称
   1. 可以描述两个元素是否等价
2. 等价类：等价元素形成的集合（对于某一类来说，可以从任意的等价元素选取一个当代表元）
3. 商集：A/R，也就是等价类的集合
4. 划分：不包含空集 + 子集并起来是整个集合 + 子集无交集
5. 偏序关系：自反、传递、反对称
6. 域：值域和定义域的并集
7. 求复合时，如果没有能够连接的，直接舍去
8. 求传递闭包：
   1. 从1次方开始加，加到重复为止
   2. 1次方就是自己

需要注意的是：生成元的求取是从0次方开始，这个的0次方是幺元，1次方是自己

• 群

1. 群：封闭 + 结合 + 幺元 + 逆元
2. 独异点：封闭 + 结合 + 幺元
3. 半群：封闭 + 结合
4. Abel群：封闭 + 结合 + 交换 + 幺元 + 逆元
5. 子群：封闭 + 逆元
6. 同构：保持运算 + 双射 + （保持常元）
   1. 双射：单射（单调） + 满射（一个y一个x）
7. 同态：提供的信息就是保持运算
   1. 保持运算：
      1. 一个元：运算符号可以放到外面
      2. 两个元：括号内的运算 = 两个括号的运算
8. 同余：关系等价 + 交换
   1. 交换：两个关系进行运算，得到的新关系仍要符合这个关系
9. 零元和任意元素运算结果是零元
10. 求幺元时，让其中一个元素等于右值即可

• 握手定理：

图的度数是边数的2倍（一个边提供2度）

• 在图中，度数为奇数的顶点有偶数个
• 一个图中，最大度 < n（结点个数）
• 无向完全图的边数：n(n-1) / 2
• 平凡图：一阶零图（只有一个顶点）
• 欧拉通路：通过所有边一次
  1. 无向图+连通+无奇度顶点 = 欧拉图
  2. 有向图+强连通+入度=出度 = 欧拉图
• 哈密顿通路：通过顶点一次
  1. 半xxx图：只能通路，不能回路
  2. 两不相邻顶点度数之和≥n，存在回路；≥n-1，存在通路（充分条件）
• 最短路径：迪杰斯特拉算法
• 树（本质是连通无回路无向图）
  1. 无回路 + m=n-1（m是边，n是顶点)
  2. 连通 + m=n-1（与完全图的n(n-1) /  2不同）
  3. 若为非平凡树，则最少2片树叶
  4. 无向图 + 连通 = 具有生成树
  5. 已知每个度的节点数，求某个度数的节点数：
     1. m = n – 1
     2. 度数和 = 2 * m
     3. 可得：度数和 = 2(n-1)
• 最小生成树：（普利姆算法）
  1. 给权排序
  2. 描点，将边数置零
  3. 选边(权最小，且不构成回路)  
  4. 一直重复第三步，直到边数=顶点数-1结束
• 最优二叉树（哈夫曼算法）
  1. 左0右1
  2. 不能构成前缀码：看两位三位的前几位有没有单独出现
  3. 哈夫曼算法
     1. 给权排序
     2. 选出两个权最小的顶点，添加新点，权为两点之和
     3. 重复步骤D2，直到只有一个顶点
     4. 注意：最小权值是将所有分支结点权值相加