CRC 循环冗余检验作为一个重点,也是数据链路层必考的一个考点,所以我把差错检测单独拿出来分析一起看一下。总结不易,一个简单的攒,Thanks♪(・ω・)ノ
目录
一、介绍及工作原理
二、校验计算过程
一、介绍及工作原理
循环冗余校验 CRC 是数据链路层的一种差错控制技术。在数据的传输过程中可能会产生比特错误(1 可能变成 0,0 可能变成 1),为了保证数据传输的可靠性,在计算机网络传输数据时,必须采用相应的差错检测机制。
在数据链路层传送的帧中,广泛使用了 CRC 技术。
在发送端,先把数据划分为组,假定每组 k 个比特;假设待传送的一组数据 M = 101001(现在 k = 6),我们在 M 后面再添加 n 位供差错检验用的冗余码一起发送。
大致计算流程如下:
① 用 2 进制的模 2 运算进行 2 ^ n 乘 M 的运算,这相当于在 M 后面添加了 n 个 0,我们设它为 M2;
② 求冗余码,用得到的 M2 除以事先选定好的长度为(n + 1)位的 P,得出的余数为 R,R 取 n 位;
③ 最后用 R 替换 M2 中最后 n 个 0 的位置,即可得出最终应传送的数据。
二、校验计算过程
已知多项式为 x^6 + x^4 + x^2 + x +1,待传送的数据串为 M = 1101011011。在 M 后面添加供差错检测用的 n 位冗余码一起发送。
第一步,确定除数 P。关于多项式,只要是 CRC 算法就离不开多项式算术,使用多项式算术是为了在二进制计算时无需考虑进位问题,CRC 校验中,多项式可以表示为,ax^5 + bx^4 + cx^3 + dx^2 + ex + 1*x^0,而 CRC 用到的除数 P,正是由多项式的各项系数组成。
展开多项式,5 次方和 3 次方系数都为 0,则 CRC 除数为 1010111。
所以为了得到除数,我们只需要观察简写式列出的项即可,为了避免出错,可以从右往左写,这个看个人习惯。
第二步,得到 M2。我们要在原数据串末端加 0,0 的数量由多项式决定,具体来说,多项式的阶数是多少就加几个 0。
例如多项式 x^6 + x^4 + x^2 + x +1,该多项式的最高次项为 6 次项,所以在已知的原数据串末端加 6 个 0,即被除数 1101011011000000 。
第三步,接下来就可以计算校验和了,模二除法。
① 将数据串的第一个 1 与除数左对齐,按位进行异或操作。

注:此过程中的计算,均不产生进位,采用相同得 0,相异的 1 的规则。
② 将未处理的数据搬下来作为新的数据串,重复操作。
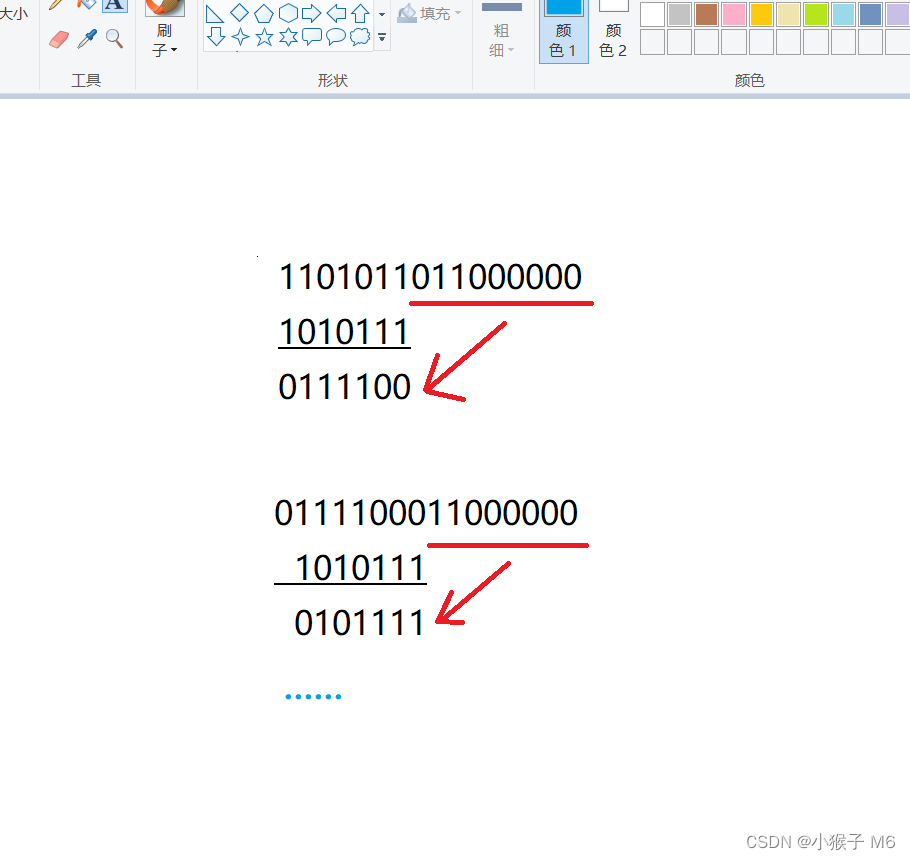
注:切记将数据串的第一个 1 与除数左对齐,头部的 0 直接跳过。
一直重复以上操作,直到所有的数据都处理过为止。所得到的结果即是校验和,也就是冗余码,111011(长度为除数-1)

第四步,将校验和加在数据项之后,便是带有 CRC 校验的数据,即最终的结果,1101011011111011。
有一处需要注意的地方是,当最后结果的有效位数较少时,最后拼接校验和的时候,不要漏掉前面的 0 ,具体来讲,所拼接的校验和的长度应与之前加 0 的个数相等。
以上是第一种考察方式,题目给出待传送的数据以及一个多项式,让你计算冗余码的过程;还有另一种考察方式就是,题目给出你的是接收方接收到的数据以及一个多项式,然后让你判断数据是否产生误码,怎么判断呢?也使用模二除法,被除数为题目已知的接收方数据,除数依然是多项式展开后的系数,异或运算后,余数为 0 没有产生误码,余数不为 0 则产生误码。


