题单介绍：

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。

题单介绍：

题目：31. 下一个排列 - 力扣（Leetcode）

题目的接口：

解题思路：

代码：

过过过过啦！！！！

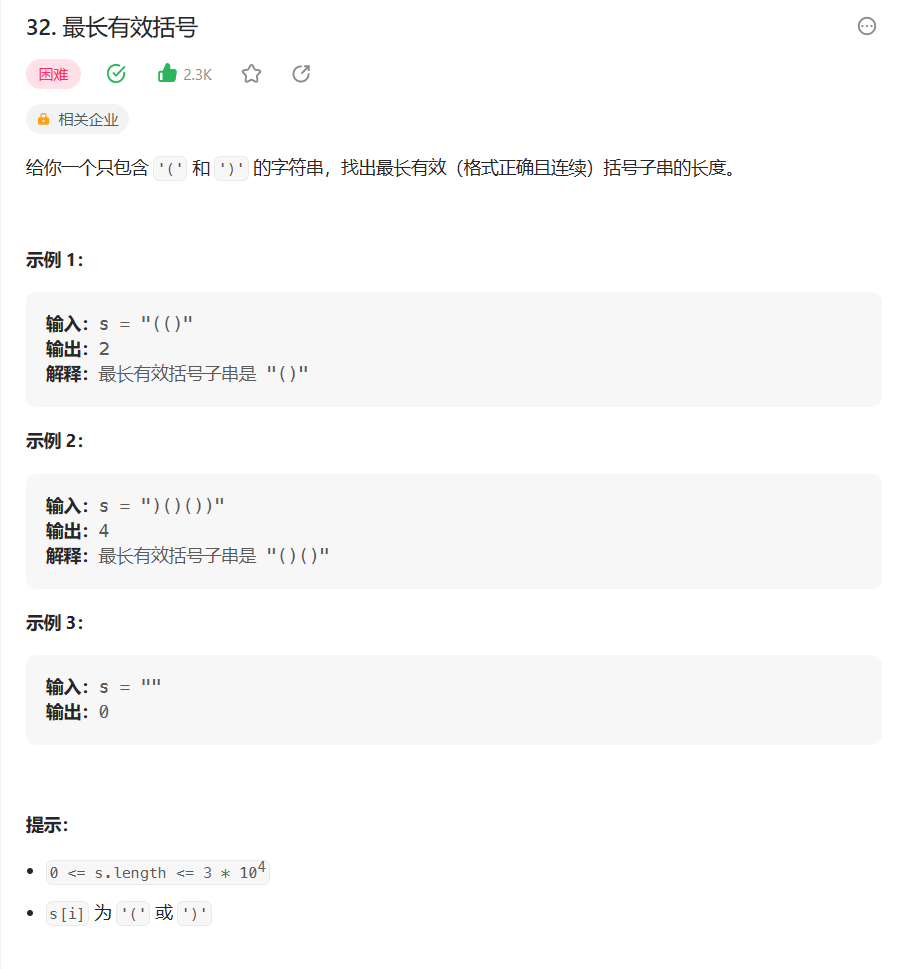
题目：32. 最长有效括号 - 力扣（Leetcode）

题目的接口：

解题思路：

代码：

过过过过啦！！！！

写在最后：

题目：31. 下一个排列 - 力扣（Leetcode）

题目的接口：

class Solution {
public:void nextPermutation(vector<int>& nums) {}
};

解题思路：

这道题的解题思路其实也不复杂，

如果降序数组，就直接排序就行，

如果数组不规律，从后往前找出比后一个数小的数，记录位置，

然后再找遍历数组，在这个位置到数组结尾这个区间找出比标记位大的数，并交换，

然后将这个区间排成升序，这样就是一个字典序最小的组合了。

代码如下：

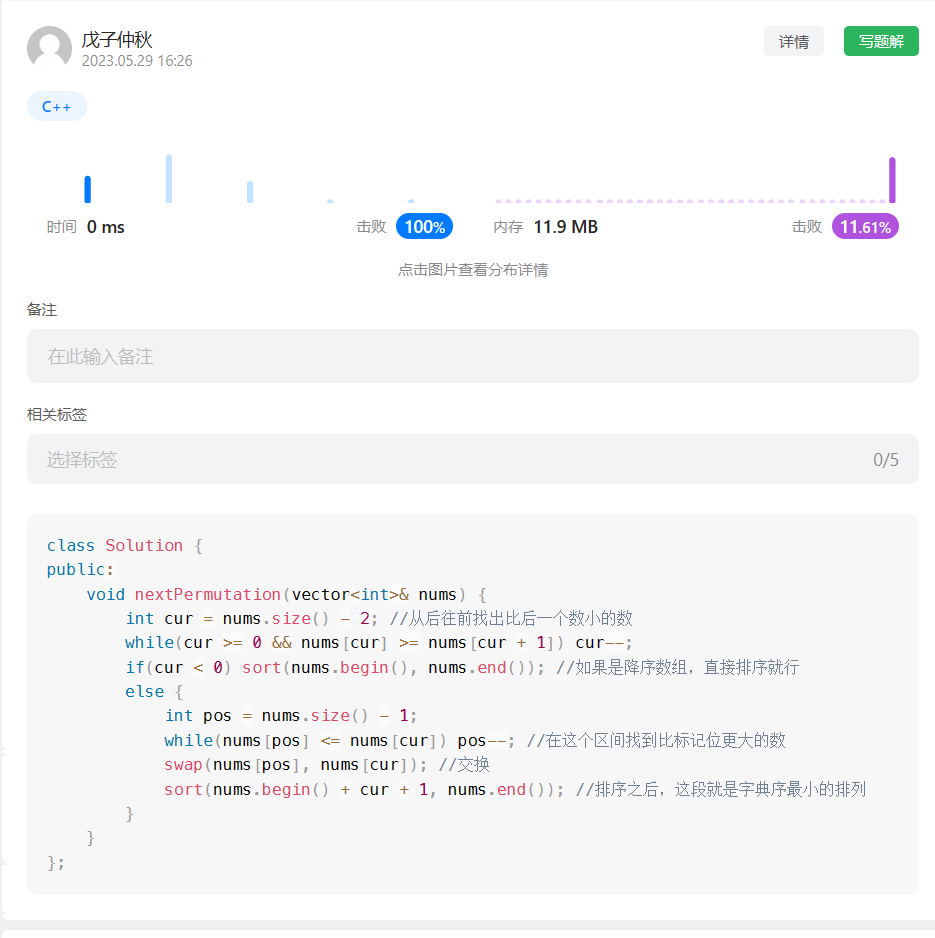
代码：

class Solution {
public:void nextPermutation(vector<int>& nums) {int cur = nums.size() - 2; //从后往前找出比后一个数小的数while(cur >= 0 && nums[cur] >= nums[cur + 1]) cur--;if(cur < 0) sort(nums.begin(), nums.end()); //如果是降序数组，直接排序就行else {int pos = nums.size() - 1;while(nums[pos] <= nums[cur]) pos--; //在这个区间找到比标记位更大的数swap(nums[pos], nums[cur]); //交换sort(nums.begin() + cur + 1, nums.end()); //排序之后，这段就是字典序最小的排列}}
};

过过过过啦！！！！

题目：32. 最长有效括号 - 力扣（Leetcode）

题目的接口：

class Solution {
public:int longestValidParentheses(string s) {}
};

解题思路：

这道题我看完之后，马上想到的思路就是用滑动窗口，

结果题解个个都是动态规划，真让人火大，

等我学会动态规划，定叫他有来无回。

总之我就用滑动窗口来做了，

思路如下：

遍历数组，

如果出现右括号的数量大于左括号，证明这段括号就不合法了，

如果出现右括号的数量等于左括号，就更新最长的序列。

如果左括号的数量一直大于右括号，可能会漏掉一些情况，比如说：

" ( ( ( ) ) " 这段序列应该更新最长序列为4，但是因为出现这种情况，导致遍历完之后更新不了。

解决方案：

我们正向遍历的时候，将所有右括号数量大于左括号的情况都遍历完了，

那么只要我们反向遍历，就能够实现把所有左括号数量大于右括号的情况遍历完，

所以只需要让现有的逻辑再走一遍反向遍历即可，这就是这个思路的核心。

代码如下：

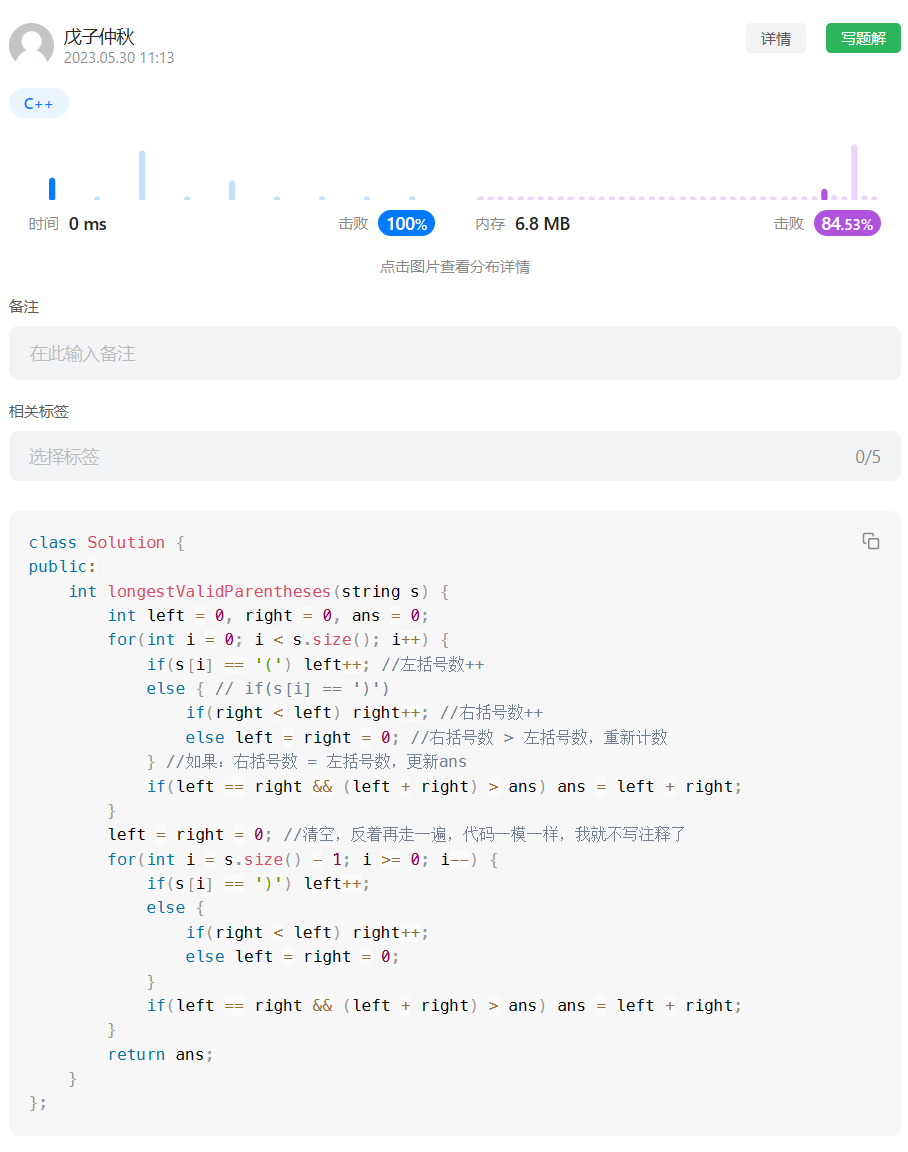
代码：

class Solution {
public:int longestValidParentheses(string s) {int left = 0, right = 0, ans = 0;for(int i = 0; i < s.size(); i++) {if(s[i] == '(') left++; //左括号数++else { // if(s[i] == ')')if(right < left) right++; //右括号数++else left = right = 0; //右括号数 > 左括号数，重新计数} //如果：右括号数 = 左括号数，更新ansif(left == right && (left + right) > ans) ans = left + right;}left = right = 0; //清空，反着再走一遍，代码一模一样，我就不写注释了for(int i = s.size() - 1; i >= 0; i--) {if(s[i] == ')') left++;else {if(right < left) right++;else left = right = 0;}if(left == right && (left + right) > ans) ans = left + right;}return ans;}
};