算法设计与分析期末复习（二）

动态规划

基本思想：把求解的问题分成许多阶段或多个子问题，然后按顺序求解各个子问题。**前一个子问题的解为后一个子问题的求解提供了有用的信息。**在求解任何一子问题时，列出各种可能的局部解，通过决策保留那些有可能达到最优的局部解，丢弃其它局部解，依次解决各子问题，最后一个子问题就是问题的解。

对于一个多阶段过程问题，最优策略是否存在，不仅依赖于该问题是否有最优子结构性质，而能否采取动态规划的方法，还要看该问题的子问题是否具有重叠性质。
最优子结构性质：原问题的最优解包含了其子问题的最优解。
子问题重叠性质：每次产生的子问题并不总是新问题，有些子问题被反复计算多次。

动态规划基本步骤

找出最优解的性质，并刻画其结构特征。
递归地定义最优值。
以自底向上的方式计算出最优值。
根据计算最优值时得到的信息，构造最优解。

矩阵连乘问题

穷举法
动态规划法
将矩阵连乘积Ai Ai+1Aj，简记为A[i:j]，i≤j，考虑计算A[i:j]的最优计算次序。

for(int *p,int n,int **t,int **s){for(int i = 1; i <= n; i++) m[i][i] = 0;for(int r = 2; r<= n; r++){for(int i=1; i <= n-r+1; i++){int j = i+r-1;m[i][j] = m[i][i] + m[i+1][j] + p[i-1]*p[i]*p[j];s[i][j] = i;for(int k=i+1; k < j; k++){int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];if(t <= m[i][j]){m[i][j] = t;s[i][j] = k;}}}}
}

算法的计算时间上界O(n³)，所占用的空间为O(n²)

最长公共子序列

由最长公共子序列问题的最优子结构性质建立子问题最优值的递归关系，用c[i][j]记录最长公共子序列的长度。
当i=0或j=0时，空序列是A和B的最长公共子序列。因此C[i][j]=0。
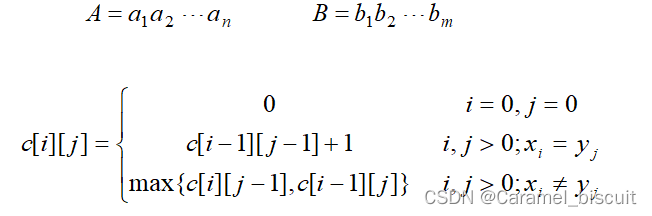
在这里插入图片描述
由于在所考虑的子问题空间中，总有θ(mn)个不同的子问题，因此用动态规划自底向上计算最优值能提高算法的效率。

void LCSLength(int m,int n,char *x,char *y,int **c,int **b){int i,j;for(i=1; i<=m; i++)	c[i][0]=0;for(i=1; i<=n; i++) c[0][i]=0;for(i=1; i<=m; i++){for(j=1; j<=n; j++){if(x[i]==y[j]){c[i][j] = x[i-1][j-1] + 1;b[i][j] = 1;}else if(c[i-1][j] >= c[i][j-1]){c[i][j] = c[i-1][j];b[i][j] = 2;}else{c[i][j] = c[i][j-1];b[i][j] = 3;}}}
}

构造最长公共子序列

void LCS(int i,int j,char *x,int **b){if(i==0 || j==0) return;if(b[i][j] == 1){LCS(i-1,j-1,x,b);printf("%d ",x[i]);}else if(b[i][j] == 2){LCS(i-1,j,x,b);}else{LCS(i,j-1,x,b);}
}

根据序列x,y，建立两个(m+1)x(n+1)的二维表C和二维表B，分别存放搜索过程中得到的子序列的长度和状态。
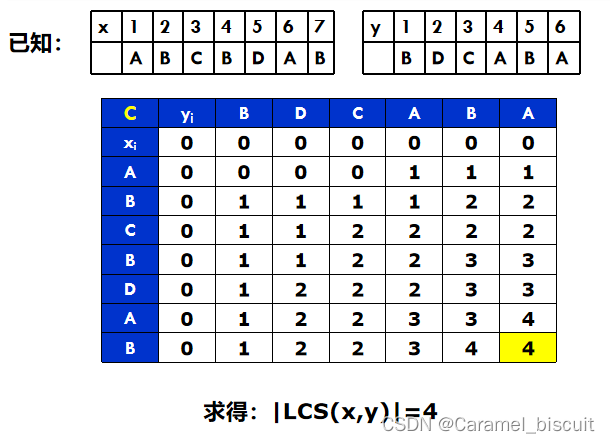
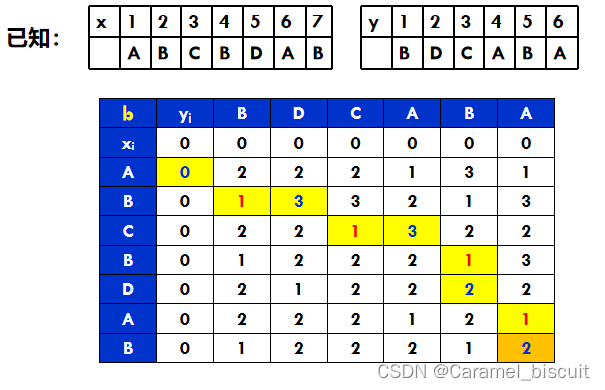
在这里插入图片描述

动态规划求解0-1背包问题

在这里插入图片描述
令V(i,j)表示前i个物品，能够装入容量为j的背包中的物品最大值。
V(i,0) = 0; 背包容量为0
V(0,j) = 0; 没有物品

如果当前物品i重量大于背包容量wi＞j，V(i,j) = V(i-1,j);
如果当前物品重量小于等于背包容量wi≤j，V(i,j) = max{V(i-1,j) , V(i-1,j-wi)+vi};

void KnapSack(int n,int w[],int v[][]){int i,j;for(i=0; i<=n; i++)	v[i][0] = 0;for(j=0; j<=c; j++) v[0][j] = 0;for(i=1; i<=n; i++){for(j=1; j<=c; j++){if(w[i] > j){v[i][j] = v[i-1][j];}else{v[i][j] = max{v[i-1][j] , v[i-1][j-w[i]]+v[i]};}}}// 求装入背包的物品j = c;for(i=n;i>=0;i--){if(v[i][j] > v[i-1][j]){x[i] = 1;j = j - w[i];}else{x[i] = 0;}}return v[n][c];
}

贪心算法

贪心算法总是做出在当前看来最好的选择，即所作的选择是局部最优解。
希望从局部的最优解得到整体最优解。
采用逐步构造最优解的方法。在每个阶段，都作出一个看上去最优的策略（在一定的标准下）。决策一旦做出，就不可以再更改。

贪心算法求解问题的基本要素

最优子结构性质：原问题的最优解包含了子问题的最优解。
贪心选择性质：原问题的最优解可以由一系列局部最优的选择来获得。

贪心算法与动态规划算法之间的差异

相同点：都具有最优子结构性质
区别：动态规划算法每步所做出的选择往往依赖于相关子问题的解，只有解除相关子问题才能做出选择。贪心算法仅在当前状态下做出最好选择，即局部最优选择，但不依赖于子问题的解。
贪心：自顶向下
动态规划：自底向上

活动安排问题

已知n个活动E={1,2,…,n}要求使用同一资源，第k个活动要求的开始时间和结束时间为sk和fk，其中sk<fk，活动k与活动j相容，sk≥fj或sj≥fk
活动安排问题就是在所给的活动集合中选出最大的相容活动子集。

基本思路
在安排时将结束时间早的活动尽量往前安排，好给后面的活动安排留出更多的空间，从而达到安排最多活动的目标。
贪心准则：在未安排的活动中挑选结束时间最早的活动安排

首先将安排的11个活动的开始时间和结束时间按结束时间的非减次序列排序：
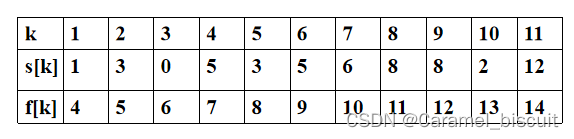
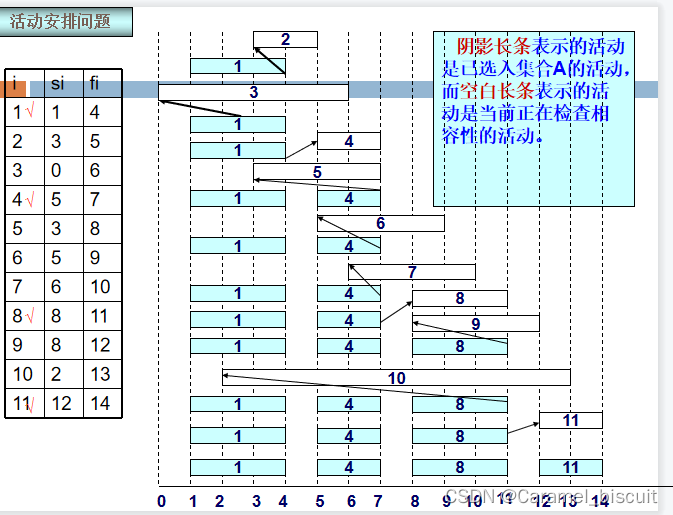
在这里插入图片描述

各活动的开始时间和结束时间已经按结束时间的非减序排列了。
public static void greedySelector(int s[], int f[], bool a[]){int n = s.length - 1;a[0] = true;int j = 0; //已经安排的最后一个活动int count = 1;for(int i=1; i<=n; i++){if(s[i] >= f[j]){a[i] = true;j = i;count++;}else{a[i] = false;}}return count;
}

0-1背包问题不能用贪心算法求解，因为0-1背包问题无法保证最终能将背包装满，部分闲置的背包空间使单位背包空间的价值降低了。

用贪心算法解决背包问题

在选择物品i装入背包时，可以选择物品i的一部分，而不一定要全部装入背包。
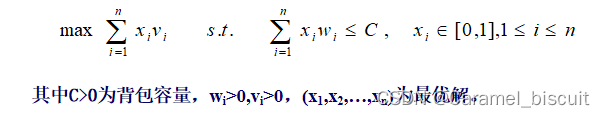
在这里插入图片描述
用贪心算法解决背包问题的基本思想：

计算每种物品单位重量的价值vi/wi，然后依贪心选择策略，尽可能多的将单位重量价值最高的物品装入背包。若这种物品全部装入背包后，背包内的物品总重量未超过C，则选择单位重量价值次高的物品并尽可能多地装入背包。依此策略一直进行下去，直到使背包装满为止，若最后一个物品不能全部装入，仅装其一部分即可。

void Knapsack(int n, float M,float v[], float w[], float x[]){sort(n,v,w);//将物品按单位重量价值排序int i;for(i=1; i<=n; i++) x[i] = 0;float c = M;for(i=1; i<=n; i++){if(w[i] > c){break;}x[i] = 1;c = c-w[i];}if(i<=n){x[i] = c/w[i];}
}