二阶张量在特定方向的投影
法向和切向分量
二阶张量T投影到 n ^ \hat n n^方向的结果是 t ⃗ ( n ^ ) = T ⋅ n ^ \vec t^{(\hat n)}=T \cdot \hat n t(n^)=T⋅n^,其中 t ⃗ ( n ^ ) \vec t^{(\hat n)} t(n^)可以分解成:
t ⃗ ( n ^ ) = T ⃗ N + T ⃗ S \vec t^{(\hat n)}=\vec T_N+\vec T_S t(n^)=TN+TS
其中, T ⃗ N \vec T_N TN是法向量, T ⃗ S \vec T_S TS是切向量
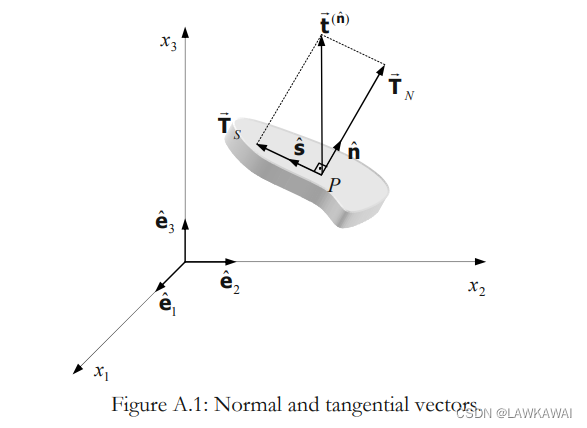
如果记 n ^ \hat n n^和 s ^ \hat s s^是 T ⃗ N \vec T_N TN和 T ⃗ S \vec T_S TS方向的单位向量,那么可以表示成:
t ⃗ ( n ^ ) = T N n ^ + T S s ^ \vec t^{(\hat n)}=T_N\hat n+T_S\hat s t(n^)=TNn^+TSs^
其中, T N T_N TN和 T S T_S TS是 T ⃗ N \vec T_N TN和 T ⃗ S \vec T_S TS的大小
向量 T ⃗ N \vec T_N TN如下所示:
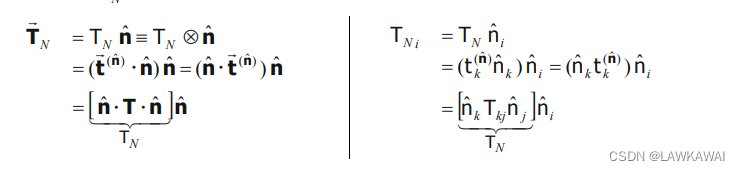
因此:
T N = t ⃗ ( n ^ ) ⋅ n ^ = n ^ ⋅ T ⋅ n ^ = n ^ k T k j n ^ j T_N = \vec t^{(\hat n)}\cdot \hat n=\hat n \cdot T \cdot \hat n=\hat n_kT_{kj}\hat n_j TN=t(n^)⋅n^=n^⋅T⋅n^=n^kTkjn^j
之前有讨论过,若对于所有的 n ^ ≠ 0 \hat n \neq 0 n^=0,有 T N = n ^ ⋅ T ⋅ n ^ > 0 T_N=\hat n \cdot T\cdot \hat n>0 TN=n^⋅T⋅n^>0,则 T T T是正定张量,并且可以表示成: T N = n ^ ⋅ T ⋅ n ^ = n ^ ⋅ T s y m ⋅ n ^ T_N = \hat n \cdot T \cdot \hat n=\hat n \cdot T^{sym} \cdot \hat n TN=n^⋅T⋅n^=n^⋅Tsym⋅n^
所以,如果一个张量的对称部分是正定的,那么这个张量也是正定的
向量 T ⃗ S \vec T_S TS可以表示成:
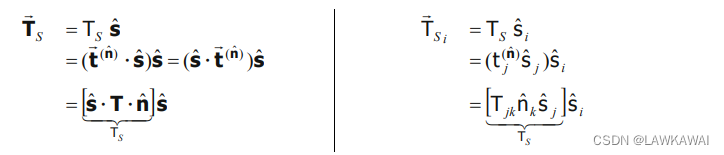
也可以表示成如下所示:
T ⃗ S = t ⃗ ( n ^ ) − T ⃗ N = T ⋅ n ^ − [ T : ( n ^ ⨂ n ^ ) ] n ^ \vec T_S = \vec t^{(\hat n)}-\vec T_N=T\cdot \hat n-[T:(\hat n \bigotimes \hat n)]\hat n TS=t(n^)−TN=T⋅n^−[T:(n^⨂n^)]n^
T ⃗ S \vec T_S TS的大小可以由勾股定理得到:
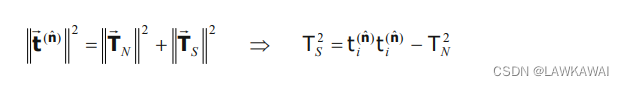
其中: t i ( n ^ ) t i ( n ^ ) = T i j T i k n j n k t_i^{(\hat n)}t_i^{(\hat n)}=T_{ij}T_{ik}n_jn_k ti(n^)ti(n^)=TijTiknjnk
思考:在哪个平面才是最大的法向和切向分量?
问题A.1 证明 T ⃗ S = t ⃗ ( n ^ ) ⋅ ( 1 − n ^ ⨂ n ^ ) \vec T_S = \vec t^{(\hat n)}\cdot (1-\hat n\bigotimes \hat n) TS=t(n^)⋅(1−n^⨂n^),其中 t ⃗ ( n ^ ) \vec t ^{(\hat n)} t(n^)就是二阶张量 T T T投影到方向 n ^ \hat n n^的结果, T ⃗ S \vec T_S TS是切向向量

法向分量的最大和最小值
法向分量为 T N = n ^ ⋅ T ⋅ n ^ T_N = \hat n\cdot T \cdot \hat n TN=n^⋅T⋅n^,满足 n ^ ⋅ n ^ = 1 \hat n \cdot \hat n = 1 n^⋅n^=1约束条件。那么求在这个约束条件下 T N T_N TN的最大最小值可以使用拉格朗日乘子法:
L ( n ^ , μ ) = T N − μ ( n ^ ⋅ n ^ − 1 ) = n ^ ⋅ T ⋅ n ^ − μ ( n ^ ⋅ n ^ − 1 ) \mathcal{L}(\hat n, \mu)=T_N-\mu (\hat n \cdot \hat n-1)=\hat n\cdot T \cdot \hat n-\mu (\hat n \cdot \hat n-1) L(n^,μ)=TN−μ(n^⋅n^−1)=n^⋅T⋅n^−μ(n^⋅n^−1)
其中, μ \mu μ是拉格朗日乘子,那么函数 L \mathcal{L} L关于 μ \mu μ和 n ^ \hat n n^的导数为:
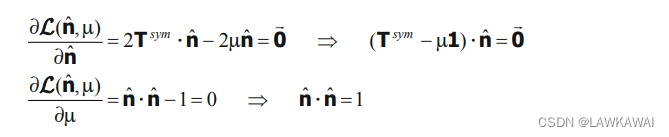
第一行有解当且仅当 det ( T s y m − 1 ) = 0 \det(T^{sym}-1)=0 det(Tsym−1)=0,这是关于张量T的对称部分的特征值问题。
也就是说, T N T_N TN的最大最小值问题跟 T s y m T^{sym} Tsym的特征值相关。
现在,假设有 T 1 s y m , T 2 s y m , T 3 s y m T_1^{sym}, T_2^{sym}, T_3^{sym} T1sym,T2sym,T3sym作为 T s y m T^{sym} Tsym的特征值,那么可以重组这些值为:
T I s y m > T I I s y m > T I I I s y m T_I^{sym}>T_{II}^{sym}>T_{III}^{sym} TIsym>TIIsym>TIIIsym
那么, T N T_N TN的最大值记为 T I s y m T_I^{sym} TIsym, 最小值记为 T I I I s y m T_{III}^{sym} TIIIsym
NOTE: 反对称部分在法向量中不起作用,因为 T N = n ^ ⋅ T ⋅ n ^ = n ^ ⋅ T s y m ⋅ n ^ T_N = \hat n \cdot T \cdot \hat n = \hat n \cdot T^{sym} \cdot \hat n TN=n^⋅T⋅n^=n^⋅Tsym⋅n^
切向分量的最大最小值
为了方便,将在T的主空间讨论,分量表示为法向分量
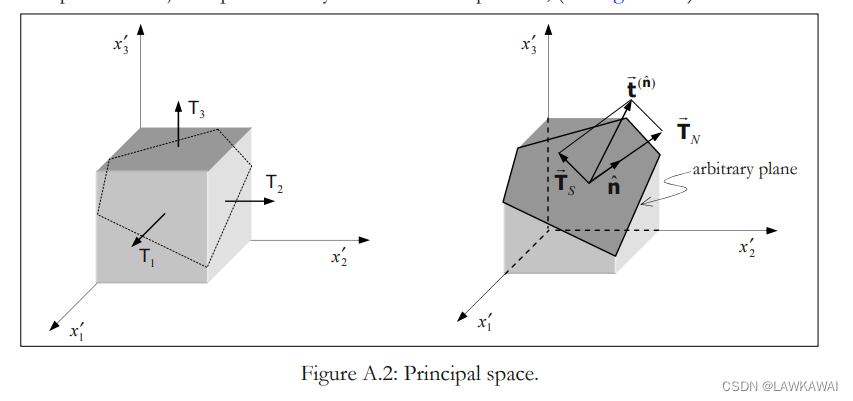
那么,方向 n ^ \hat n n^的法向分量 T N T_N TN,如下所示:
T N = t i ( n ^ ) n ^ i = T i j n ^ i n ^ j = T 1 n ^ 1 2 + T 2 n ^ 2 2 + T 3 n ^ 3 2 T_N=t_i^{(\hat n)}\hat n_i=T_{ij}\hat n_i\hat n_j=T_1\hat n_1^2+T_2\hat n_2^2+T_3\hat n_3^2 TN=ti(n^)n^i=Tijn^in^j=T1n^12+T2n^22+T3n^32
在特定的方向 n ^ i = [ 1 , 0 , 0 ] ⟹ T N = T i \hat n _i= [1, 0, 0] \implies T_N=T_i n^i=[1,0,0]⟹TN=Ti
切向分量如下所示:
T S 2 = ∣ ∣ t ⃗ ( n ^ ) ∣ ∣ 2 − T N 2 = t i ( n ^ ) t i ( n ^ ) − T N 2 = T i j T i k n ^ j n ^ k − T N 2 T_S^2=||\vec t^{(\hat n)}||^2-T_N^2=t_i^{(\hat n)}t_i^{(\hat n)}-T_N^2=T_{ij}T_{ik}\hat n_j\hat n_k-T_N^2 TS2=∣∣t(n^)∣∣2−TN2=ti(n^)ti(n^)−TN2=TijTikn^jn^k−TN2
代入 T N = t i ( n ^ ) n ^ i = T i j n ^ i n ^ j T_N=t_i^{(\hat n)}\hat n_i=T_{ij}\hat n_i\hat n_j TN=ti(n^)n^i=Tijn^in^j,有:
T S 2 = T 1 2 n 1 2 + T 2 2 n 2 2 + T 3 2 n 3 2 − ( T 1 n ^ 1 2 + T 2 n ^ 2 2 + T 3 n ^ 3 2 ) 2 T_S^2=T_1^2n_1^2+T_2^2n_2^2+T_3^2n_3^2-(T_1\hat n_1^2+T_2\hat n_2^2+T_3\hat n_3^2)^2 TS2=T12n12+T22n22+T32n32−(T1n^12+T2n^22+T3n^32)2
现在如果问: n ^ i \hat n_i n^i取什么值才能使得函数 T S 2 T_S^2 TS2等于最大最小值,这个问题等价于:
F ( n ^ ) = T S 2 − μ ( n ^ i n ^ i − 1 ) F(\hat n)=T_S^2-\mu(\hat n_i\hat n_i-1) F(n^)=TS2−μ(n^in^i−1)
其中, μ \mu μ是拉格朗日乘子,约束条件为 n ^ ⋅ n ^ = 1 \hat n \cdot \hat n = 1 n^⋅n^=1,那么:
∂ F ( n ^ ) ∂ n j = 0 j ; ∂ F ( n ^ ) ∂ μ = 0 \frac{\partial F(\hat n)}{\partial n_j}=0_j; \quad \frac{\partial F(\hat n)}{\partial \mu}=0 ∂nj∂F(n^)=0j;∂μ∂F(n^)=0
解以上方程组,得到:
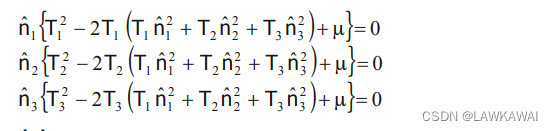
那么,可能的解如下所示:
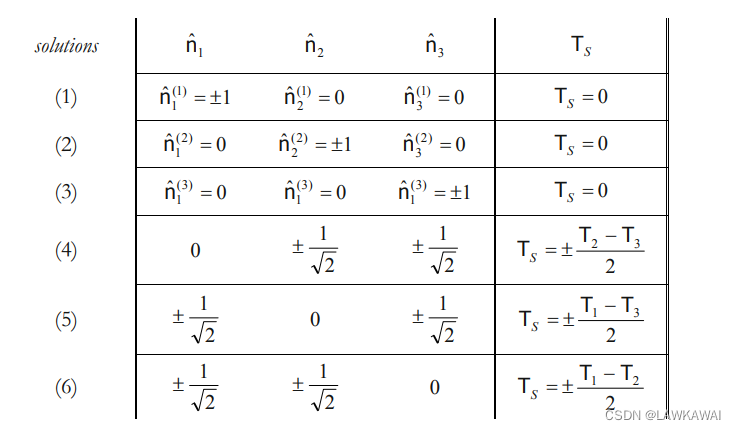
前三组解:提供了 T S T_S TS的最小值,为0,正好对应于主方向
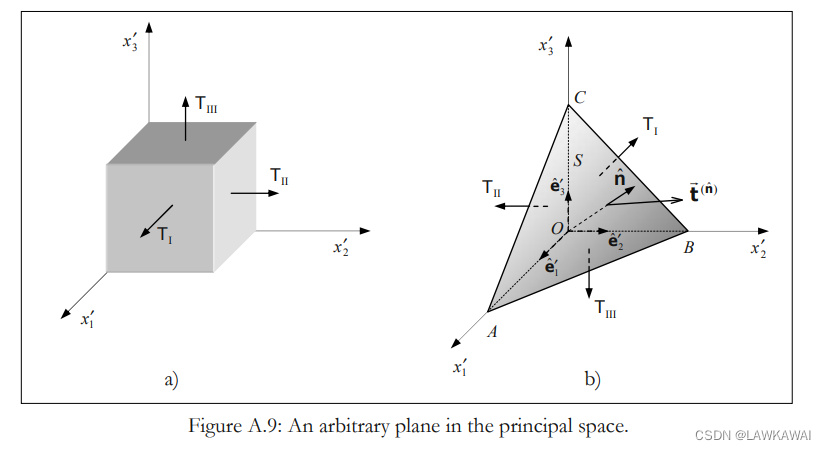
(4), (5), (6)这三组解,所表示的平面如下图所示:
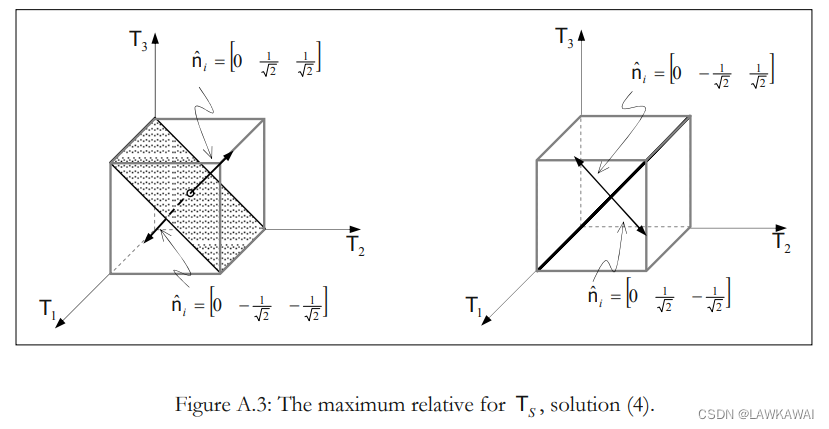
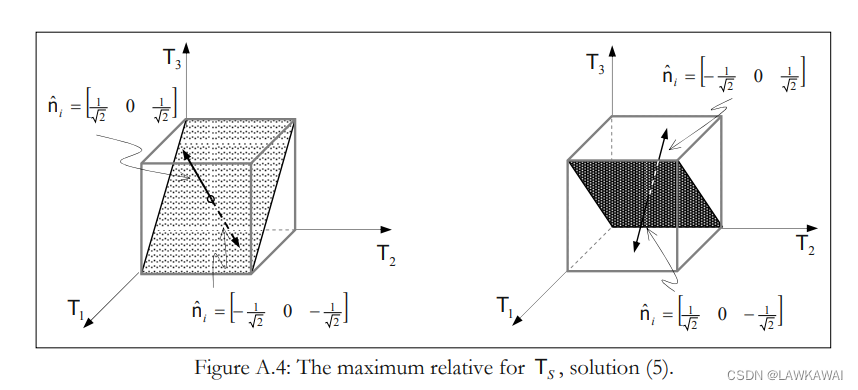
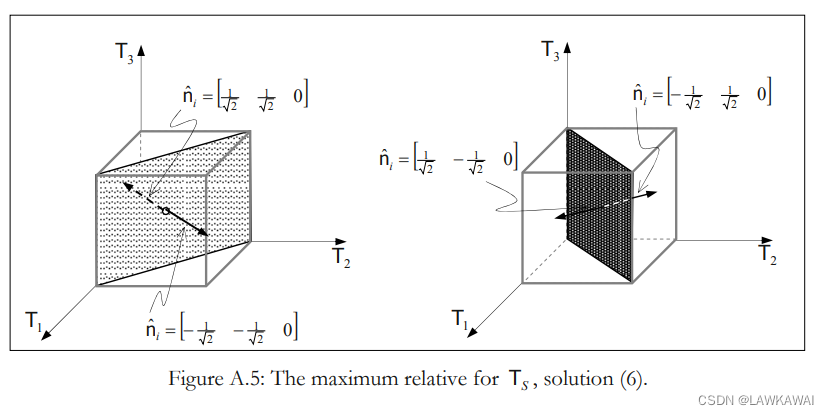
对 T 1 , T 2 , T 3 T_1, T_2, T_3 T1,T2,T3进行排序,那么, T S T_S TS可以表示成 T I , T I I , T I I I T_I, T_{II}, T_{III} TI,TII,TIII的形式:
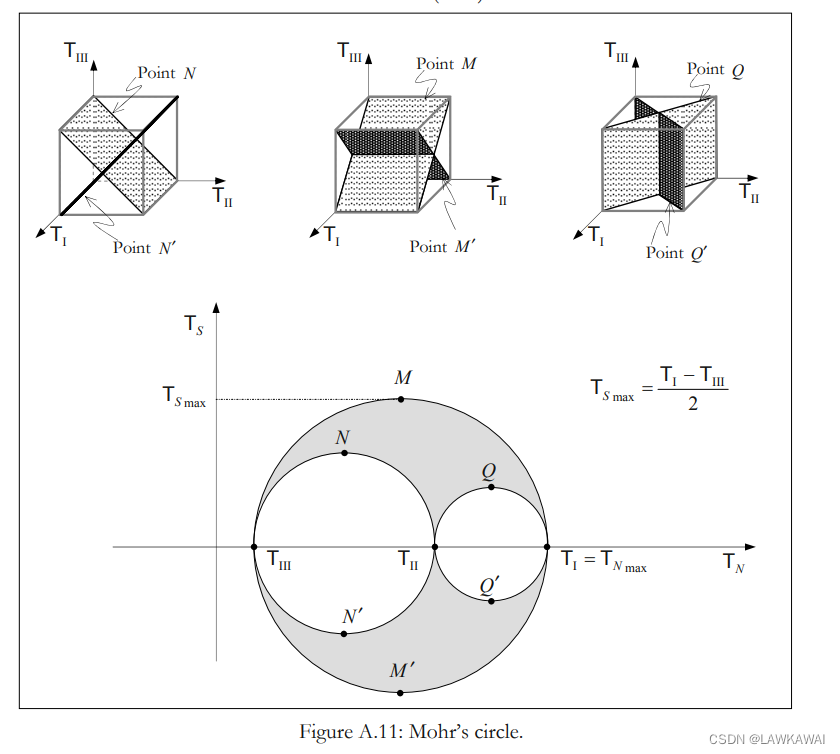
T S m a x = T I − T I I I 2 T_{Smax}=\frac{T_I-T_{III}}{2} TSmax=2TI−TIII
任意二阶张量的图像表示
如果给定一个二阶张量的笛卡尔分量,那么就可以列出在任意由法向量 n ^ \hat n n^ 定义的平面上的法向和切向分量 ( T N , T S ) (T_N, T_S) (TN,TS)
约束条件是: n ^ ⋅ n ^ = n ^ 1 2 + n ^ 2 2 + n ^ 3 2 = 1 \hat n \cdot \hat n = \hat n_1^2+\hat n_2^2+\hat n_3^2=1 n^⋅n^=n^12+n^22+n^32=1
可以画出以 T N T_N TN为横坐标, T S T_S TS为纵坐标的图像
数值过程:
先随机列举几个不同的 n ^ \hat n n^,这样就可以得到不同的 ( T N , T S ) (T_N, T_S) (TN,TS),把点画在 T N × T S T_N \times T_S TN×TS的图像中
同样,可以建立一个由其对称部分构成的图像: T N s y m × T S s y m T_N^{sym} \times T_S^{sym} TNsym×TSsym
第一个例子:对称的正定张量, T N = n ^ ⋅ T ⋅ n ^ > 0 , f o r a l l n ^ ≠ 0 ⃗ T_N = \hat n \cdot T \cdot \hat n>0, \quad for \quad all \quad \hat n \neq \vec 0 TN=n^⋅T⋅n^>0,foralln^=0
可以证明,有三个特征值对应的是 T S = 0 T_S = 0 TS=0
由下图可以看出, T N T_N TN的最大最小值对其对称部分的最大最小值

对于切向向量,可以得到以下分解:
T ⃗ S = [ s ^ ⋅ T ⋅ n ^ ] s ^ = [ s ^ ⋅ T s y m ⋅ n ^ + s ^ ⋅ T s k e w ⋅ n ^ ] s ^ \vec T_S = [\hat s \cdot T \cdot \hat n]\hat s=[\hat s \cdot T^{sym}\cdot \hat n+\hat s \cdot T^{skew}\cdot \hat n]\hat s TS=[s^⋅T⋅n^]s^=[s^⋅Tsym⋅n^+s^⋅Tskew⋅n^]s^
当 n ^ \hat n n^ 是对称部分的其中的一个主方向时,有:

其中 s ^ ⋅ n ^ = 0 \hat s \cdot \hat n = 0 s^⋅n^=0,因为单位向量 s ^ \hat s s^和 n ^ \hat n n^是正交的
所以,切向分量如下所示:
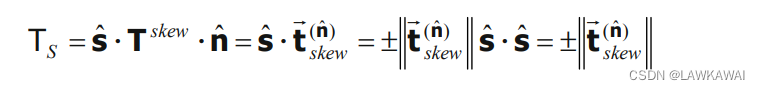
以上公式仅适用于 n ^ \hat n n^是 T s y m T^{sym} Tsym主方向的其中一个
对于特征值 T I s y m = 10.55 T_I^{sym}=10.55 TIsym=10.55,对应的特征向量 n ^ j ( 1 ) = [ − 0.4522937 ; − 0.561517458 ; 0.692913086 ] \hat n_j^{(1)}=[-0.4522937; -0.561517458; 0.692913086] n^j(1)=[−0.4522937;−0.561517458;0.692913086],有:

而对于特征值 T I I s y m = 3.61 T_{II}^{sym}=3.61 TIIsym=3.61, 有:
s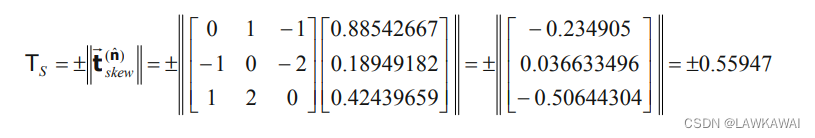
对于特征值 T I I I s y m = 0.84 T_{III}^{sym}=0.84 TIIIsym=0.84, 有:

可以发现,T的最大和最小的法向分量对应的是 T s y m T^{sym} Tsym的特征值,
例如, T N m a x = T I s y m = 10.55 T_{N_{max}}=T_I^{sym}=10.55 TNmax=TIsym=10.55, T N m i n = T I I I s y m = 0.84 T_{N_{min}}=T_{III}^{sym}=0.84 TNmin=TIIIsym=0.84
那么最大的切向分量等于圆的半径,即由 T I s y m = 10.55 T_I^{sym}=10.55 TIsym=10.55 和 T I I I s y m = 0.84 T_{III}^{sym}=0.84 TIIIsym=0.84构成的:
T S m a x s y m = 10.55 − 0.84 2 = 4.86 T_{S_{max}}^{sym}=\frac{10.55-0.84}{2}=4.86 TSmaxsym=210.55−0.84=4.86
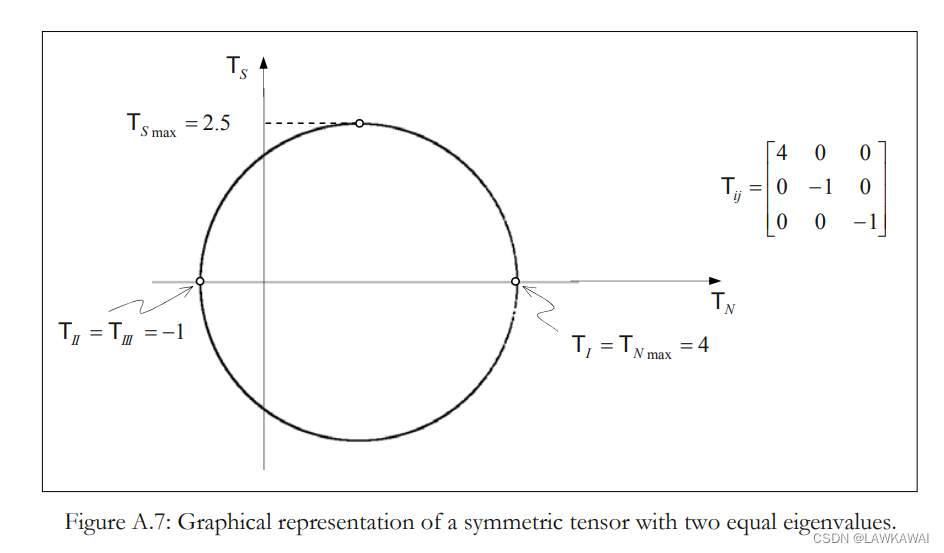
第二个例子:
对称张量有两个相同的特征值,可以验证 ( T N , T S ) (T_N, T_S) (TN,TS)可取的值被限制在以半径 R = T I − T I I I 2 = 2.5 R = \frac{T_I-T_{III}}{2}=2.5 R=2TI−TIII=2.5, 以及圆中心为 ( T N = T I + T I I I 2 = 1.5 , T S = 0 ) (T_N=\frac{T_I+T_{III}}{2}=1.5, T_S=0) (TN=2TI+TIII=1.5,TS=0)上的圆
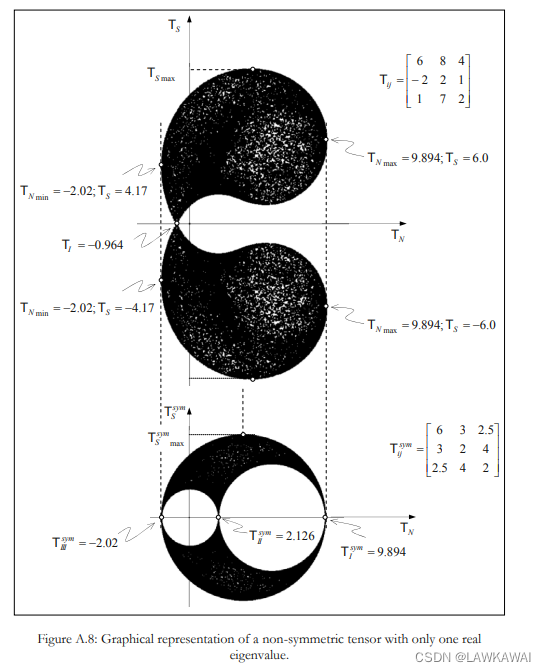
第三个例子:非对称张量
只有一个实数特征值,为 T I = − 0.964 T_I= -0.964 TI=−0.964
在T的对称部分的主方向上,可以列出切向分量的值:
对于特征值 T I s y m = 9.894 T_{I}^{sym}=9.894 TIsym=9.894,有:

对于特征值 T I I I s y m = − 2.02 T_{III}^{sym}=-2.02 TIIIsym=−2.02, 有:

对称二阶张量的图像表示(莫尔圆)
有:
T S 2 + T N 2 = t ⃗ ( n ^ ) ⋅ t ⃗ ( n ^ ) = ∣ ∣ t ⃗ ( n ^ ) ∣ ∣ 2 T_S^2+T_N^2=\vec t^{(\hat n)}\cdot \vec t^{(\hat n)}=||\vec t ^{(\hat n)}||^2 TS2+TN2=t(n^)⋅t(n^)=∣∣t(n^)∣∣2
主空间的 t ⃗ ( n ^ ) = T ⋅ n ^ \vec t^{(\hat n)}=T \cdot \hat n t(n^)=T⋅n^的分量,由下给出:
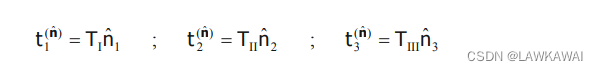
那么点乘 t ⃗ ( n ^ ) ⋅ t ⃗ ( n ^ ) \vec t^{(\hat n)} \cdot \vec t^{(\hat n)} t(n^)⋅t(n^), 如下所示:
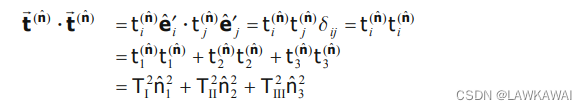
那么:
T S 2 + T N 2 = T I 2 n ^ 1 2 + T I I 2 n ^ 2 2 + T I I I 2 n ^ 3 2 T_S^2+T_N^2 = T_I^2\hat n_1^2+T_{II}^2\hat n_2^2+T_{III}^2\hat n_3^2 TS2+TN2=TI2n^12+TII2n^22+TIII2n^32
那么,在主空间的法向分量 T N T_N TN,可以写成:
T N = t ⃗ ( n ^ ) ⋅ T = T i j n ^ i n ^ j = T I n ^ 1 2 + T I I n ^ 2 2 + T I I I n ^ 1 2 T_N = \vec t ^{(\hat n)} \cdot T=T_{ij}\hat n_i\hat n_j=T_I\hat n_1^2+T_{II}\hat n_2^2+T_{III}\hat n_1^2 TN=t(n^)⋅T=Tijn^in^j=TIn^12+TIIn^22+TIIIn^12
考虑约束条件: n ^ i n ^ i = 1 ⟹ n ^ 1 2 = 1 − n ^ 2 2 − n ^ 3 2 \hat n_i \hat n_i=1 \implies \hat n_1^2 = 1-\hat n_2^2-\hat n_3^2 n^in^i=1⟹n^12=1−n^22−n^32, 代入到上式,求出 n ^ 2 2 \hat n_2^2 n^22:
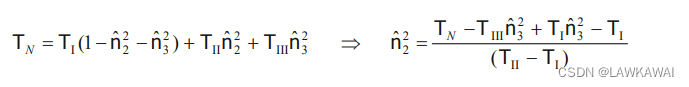
n ^ 1 2 = 1 − n ^ 2 2 − n ^ 3 2 \hat n_1^2 = 1-\hat n_2^2-\hat n_3^2 n^12=1−n^22−n^32代入公式:
T S 2 + T N 2 = T I 2 n ^ 1 2 + T I I 2 n ^ 2 2 + T I I I 2 n ^ 3 2 T_S^2+T_N^2 = T_I^2\hat n_1^2+T_{II}^2\hat n_2^2+T_{III}^2\hat n_3^2 TS2+TN2=TI2n^12+TII2n^22+TIII2n^32
可得:
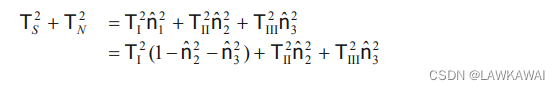
再代入 n ^ 2 2 \hat n_2^2 n^22,得:
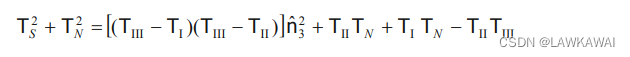
得到 n ^ 3 2 \hat n_3^2 n^32:
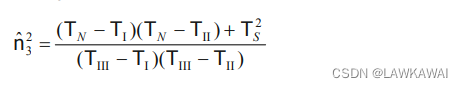
所以,也可以用相似得方式求出 n ^ 1 2 \hat n_1^2 n^12 和 n ^ 2 2 \hat n_2^2 n^22, 如下所示:
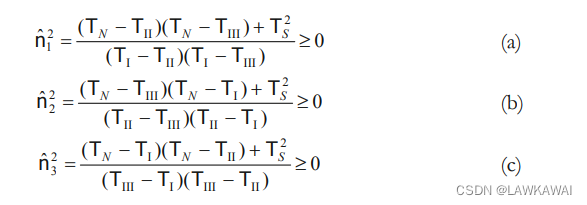
若 T I > T I I > T I I I T_I > T_{II} > T_{III} TI>TII>TIII, (a)和©的分母都为正,那么分子也为正;(b)分母为负,那么分子也必须为负
例如:
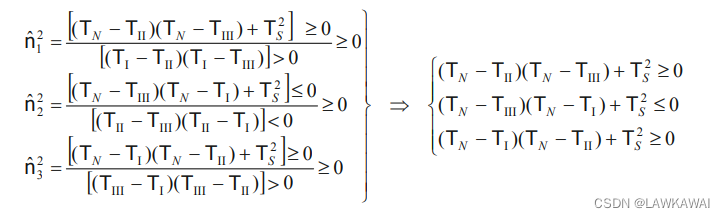
经过代数变换:
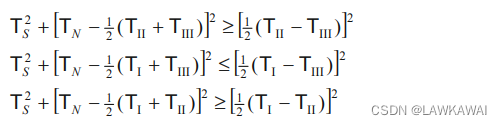
以上的等式表示是圆
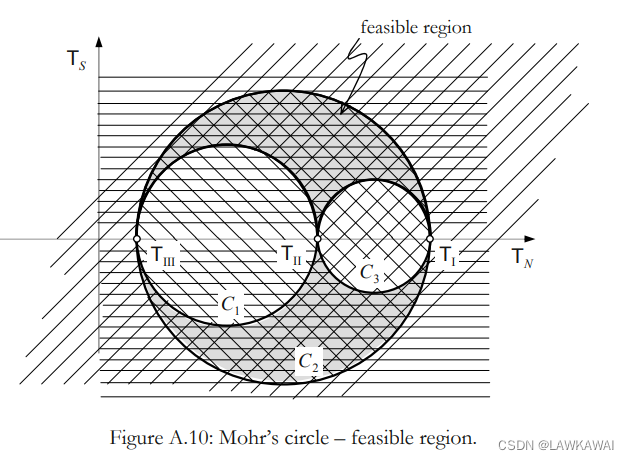
第一个圆
中心: ( 1 2 ( T I I + T I I I ) , 0 ) (\frac{1}{2}(T_{II}+T_{III}), 0) (21(TII+TIII),0)
半径: 1 2 ( T I I − T I I I ) \frac{1}{2}(T_{II}-T_{III}) 21(TII−TIII)
第一个可行域是在圆 C 1 C_1 C1之外:
第二个圆
中心: ( 1 2 ( T I + T I I I ) , 0 ) (\frac{1}{2}(T_{I}+T_{III}), 0) (21(TI+TIII),0)
半径: 1 2 ( T I − T I I I ) \frac{1}{2}(T_{I}-T_{III}) 21(TI−TIII)
第二个可行域是在圆 C 2 C_2 C2之内:
第三个圆
中心: ( 1 2 ( T I + T I I ) , 0 ) (\frac{1}{2}(T_{I}+T_{II}), 0) (21(TI+TII),0)
半径: 1 2 ( T I − T I I ) \frac{1}{2}(T_{I}-T_{II}) 21(TI−TII)
第三个可行域是在圆 C 3 C_3 C3之外:
所以,可行域如下所示:
在莫尔圆中,最大值 T S m a x T_{S_{max}} TSmax的解:
张量椭球
对称二阶张量T在主空间的特征值 ( T 1 , T 2 , T 3 ) (T_1, T_2, T_3) (T1,T2,T3) , 满足以下:
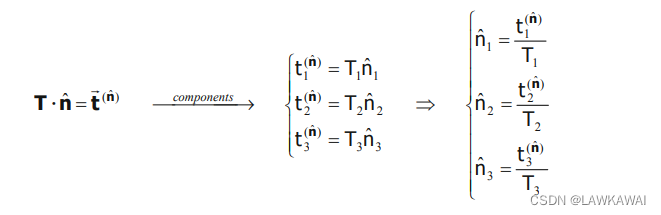
现在,在主空间定义一个曲面,这个曲面可以描述 n ^ \hat n n^ 的所有可能值得向量 t ⃗ ( n ^ ) \vec t ^{(\hat n)} t(n^)
由约束条件: n ^ 1 2 + n ^ 2 2 + n ^ 3 2 = 1 \hat n_1^2+ \hat n_2^2+\hat n_3^2=1 n^12+n^22+n^32=1, 有:
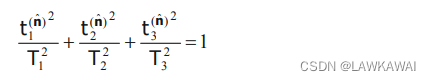
这个表示得是一个在T主空间得椭球。如下所示
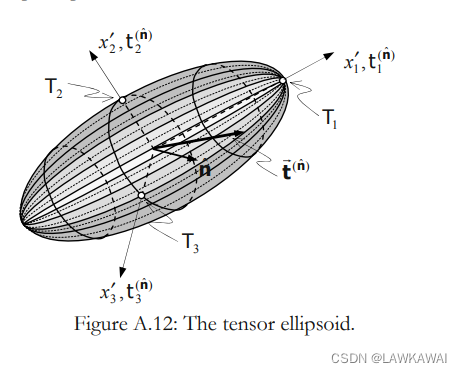
椭球表面表示的是 t 1 , t 2 , t 3 t_1, t_2, t_3 t1,t2,t3的可能取值
当两个特征值相等,那么就会得到一个旋转的椭球
当三个特征值相等,那么得到一个球, 此时表现出这种性质的张量被称为球面张量,任意方向都是主方向
球面张量和偏张量的图像表示
八面体向量
八面体平面,又称作偏平面,在这个平面上的法向与主方向的夹角都相等
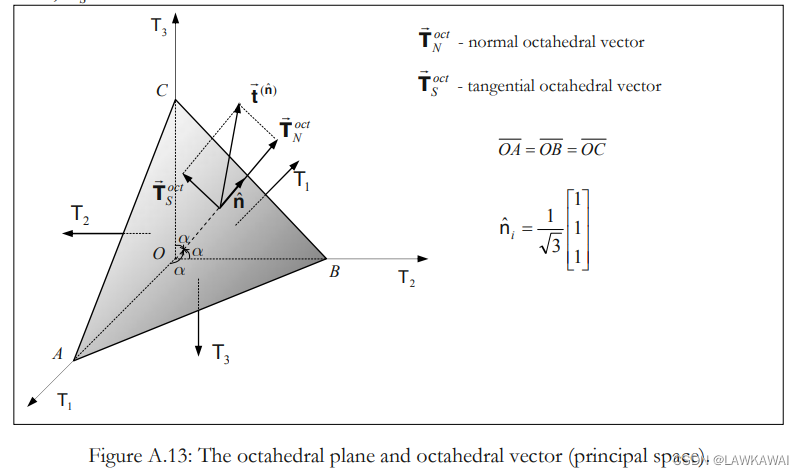
n ^ 1 = n ^ 2 = n ^ 3 \hat n_1=\hat n_2 = \hat n_3 n^1=n^2=n^3, 有: 3 n ^ 1 2 = 1 3\hat n_1^2=1 3n^12=1 , 所以:
n ^ i = [ 1 3 1 3 1 3 ] \hat n_i= [\frac{1}{\sqrt{3}} \quad \frac{1}{\sqrt{3}} \quad \frac{1}{\sqrt{3}}] n^i=[313131]
二阶张量投影到一个八面体平面得到的向量,标记为八面体向量 t ⃗ ( n ^ ) \vec t ^{(\hat n)} t(n^), 可以分解为法向分量和切向分量,
定义法向八面体向量 T ⃗ N o c t \vec T_N^{oct} TNoct, 切向八面体向量 T ⃗ S o c t \vec T_S^{oct} TSoct
八面体向量可以表示成:
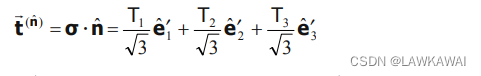
那么, T ⃗ N o c t \vec T_N^{oct} TNoct 的大小可以用 T ⃗ N o c t \vec T_N^{oct} TNoct投影到 n ^ \hat n n^来表示:
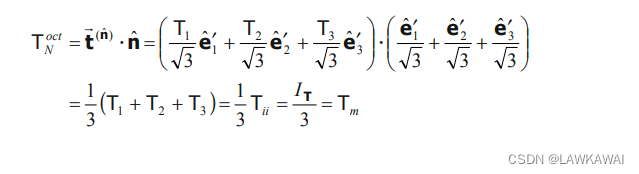
其中 T N o c t T_N^{oct} TNoct称为 八面体法向分量
那么,八面体切向分量 T S o c t T_S^{oct} TSoct,如下所示:
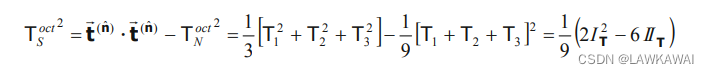
以上式子同样可以表示成:
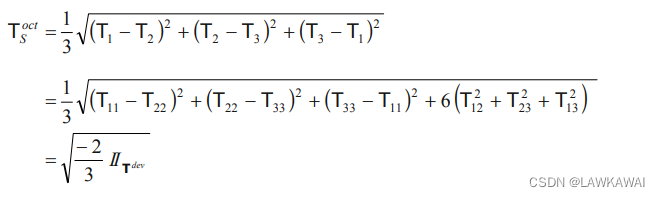
或者表示偏张量:
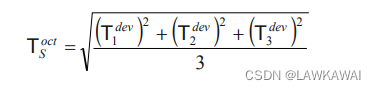
总结:
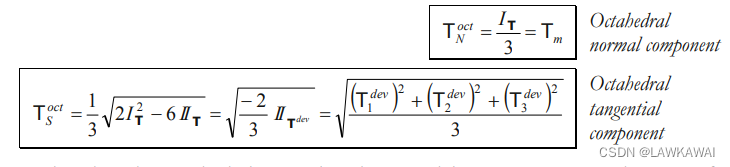
八面体法向和切向分量是8个八面体平面:
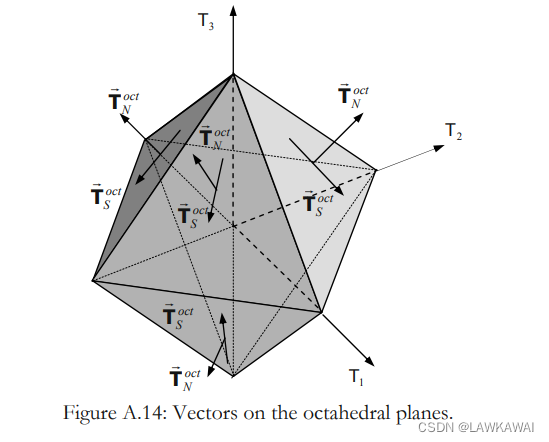
在主空间表示点 P ( T 1 , T 2 , T 3 ) P(T_1, T_2, T_3) P(T1,T2,T3),如下所示:
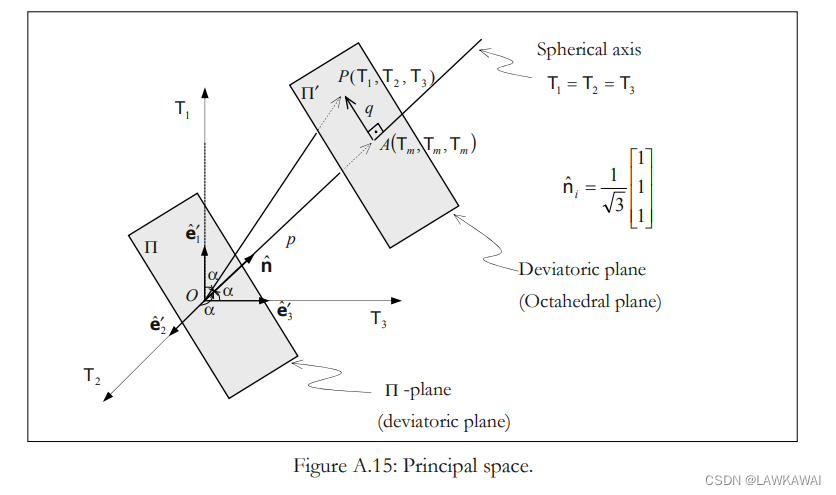
任意与直线 O A ‾ \overline{OA} OA 垂直的平面是八面体的(偏的),并且经过原点的八面体平面为 Π \Pi Π, 最后,直线 O A ‾ \overline{OA} OA 被称为球轴(净水轴)
考虑一个偏平面穿过点P,标记为 Π ′ \Pi' Π′, 定义三个向量 O P ⃗ , O A ⃗ , A P ⃗ \vec {OP}, \vec {OA}, \vec {AP} OP,OA,AP
O P ⃗ \vec {OP} OP 可以表示成T的主值:
O P ⃗ = T 1 e ^ 1 ′ + T 2 e ^ 2 ′ + T 3 e ^ 3 ′ \vec {OP} = T_1 \hat e_1'+T_2 \hat e_2'+T_3 \hat e_3' OP=T1e^1′+T2e^2′+T3e^3′
根据上面的图像, O A ⃗ \vec {OA} OA 的大小表示为:
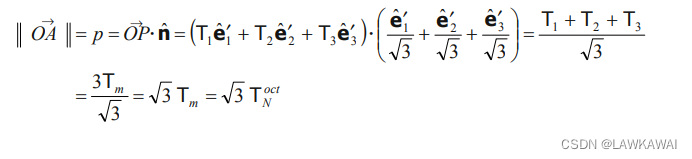
p = 3 T m = 3 T N o c t \boxed{p=\sqrt{3}T_m=\sqrt{3}T_N^{oct}} p=3Tm=3TNoct
因此,向量 O A ⃗ \vec {OA} OA 表示为:
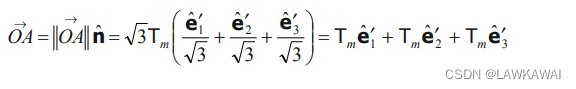
那么就可以求出 A P ⃗ \vec {AP} AP:
A P ⃗ = O P ⃗ − O A ⃗ \vec {AP} = \vec {OP} - \vec {OA} AP=OP−OA
由于:
O P ⃗ = T 1 e ^ 1 ′ + T 2 e ^ 2 ′ + T 3 e ^ 3 ′ \vec {OP} = T_1 \hat e_1'+T_2 \hat e_2'+T_3 \hat e_3' OP=T1e^1′+T2e^2′+T3e^3′
所以,有:
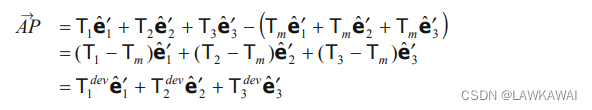
利用定义 T i j d e v = T i j − T m δ i j T_{ij}^{dev} = T_{ij}-T_m \delta_{ij} Tijdev=Tij−Tmδij,有:
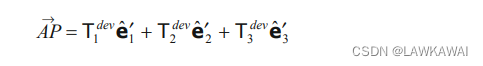
AP的分量表示的是主值的偏部分 T i j d e v T_{ij}^{dev} Tijdev
A P ⃗ \vec {AP} AP的大小为:
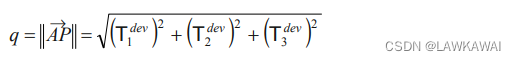
考虑 2 I I T d e v = − ( T 1 d e v ) 2 − ( T 2 d e v ) 2 − ( T 3 d e v ) 2 2II_{T^{dev}}=-(T_1^{dev})^2-(T_2^{dev})^2-(T_3^{dev})^2 2IITdev=−(T1dev)2−(T2dev)2−(T3dev)2
有:
q = − 2 I I T d e v = 3 T S o c t \boxed{q = \sqrt{-2II_{T^{dev}}}=\sqrt{3}T_S^{oct}} q=−2IITdev=3TSoct
根据毕达哥拉斯定理,也可以得到:
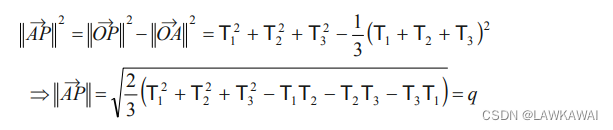
q: 表示张量状态距离球面状态的距离
考虑将主空间投影到 Π \Pi Π 平面
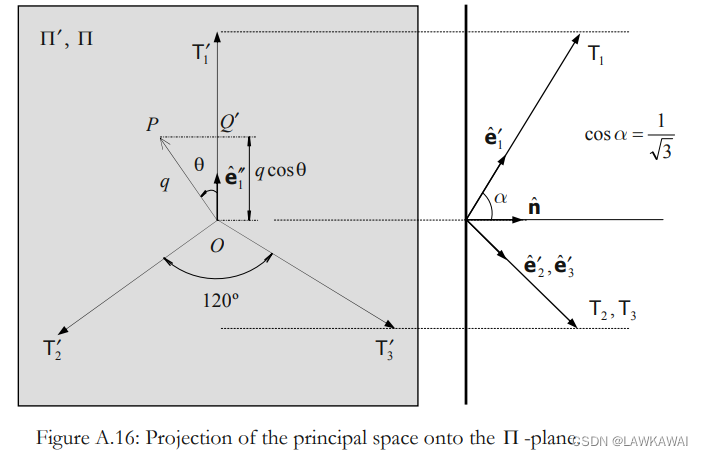
单位向量 e ^ 1 ′ ′ = a 1 e ^ 1 ′ + a 2 e ^ 2 ′ + a 3 e ^ 3 ′ \hat e_1''=a_1 \hat e_1'+a_2 \hat e_2'+a_3 \hat e_3' e^1′′=a1e^1′+a2e^2′+a3e^3′
其中: cos β = sin α = 2 3 = a 1 \cos \beta=\sin \alpha=\frac{\sqrt{2}}{\sqrt{3}}=a_1 cosβ=sinα=32=a1, a 2 = a 3 a_2 = a_3 a2=a3
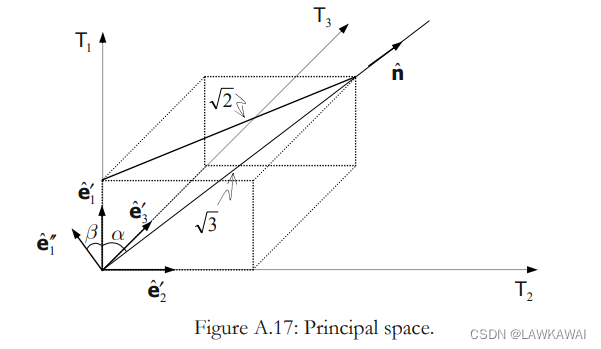
如果净水轴与偏平面是正交的,那么:
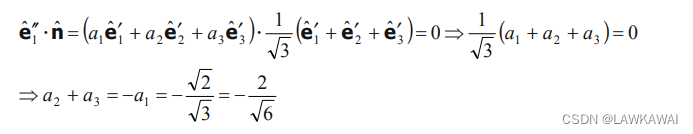
解得:
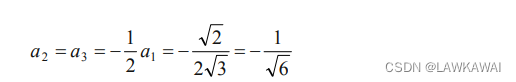
因此:
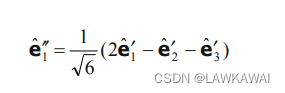
那么, O P ⃗ \vec {OP} OP 在 e ^ 1 ′ ′ \hat e_1'' e^1′′ 的投影如下所示:
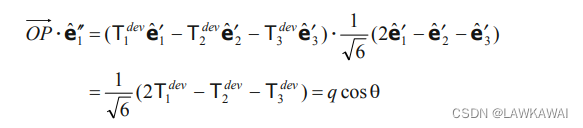
如果考虑 T 1 d e v + T 2 d e v + T 3 d e v = 0 T_1^{dev}+T_2^{dev}+T_3^{dev}=0 T1dev+T2dev+T3dev=0 , 那么 − T 1 d e v = T 2 d e v + T 3 d e v -T_1^{dev}=T_2^{dev}+T_3^{dev} −T1dev=T2dev+T3dev, 则上式变为:
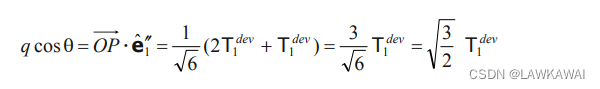
由于 q = − 2 I I T d e v q = \sqrt{-2II_{T^{dev}}} q=−2IITdev, 有:
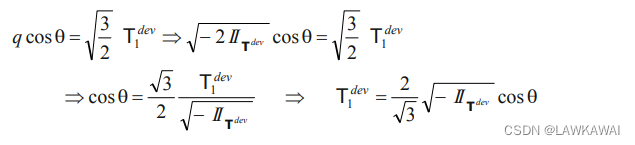
同样地,可以求出 T 2 d e v T_2^{dev} T2dev 和 T 3 d e v T_3^{dev} T3dev
那么,可以将主值表示为, T i j = T m δ i j + T i j d e v T_{ij}=T_m\delta_{ij}+T_{ij}^{dev} Tij=Tmδij+Tijdev

其中 0 ≤ θ ≤ π / 3 0 \le \theta \le \pi / 3 0≤θ≤π/3
所以,张量可以表示成 ( p , q , θ ) (p, q, \theta ) (p,q,θ)
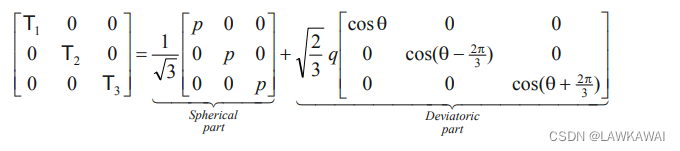
由于:
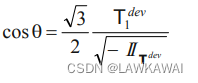
且有: cos 3 θ = 4 cos 3 θ − 3 cos θ \cos 3\theta=4\cos^3 \theta -3\cos \theta cos3θ=4cos3θ−3cosθ, 代入可得:
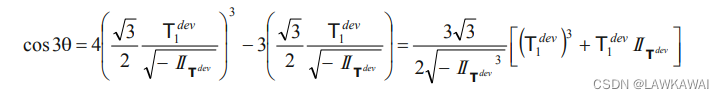
并且有: I I T d e v = ( T 1 d e v T 2 d e v + T 2 d e v T 3 d e v + T 1 d e v T 3 d e v ) II_{T^{dev}}=(T_1^{dev}T_2^{dev}+T_2^{dev}T_3^{dev}+T_1^{dev}T_3^{dev}) IITdev=(T1devT2dev+T2devT3dev+T1devT3dev)
那么:
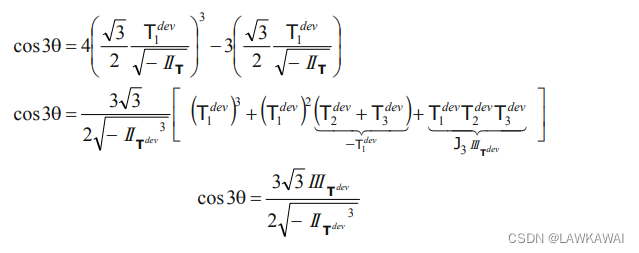
由于 I I T d e v II_{T^{dev}} IITdev 和 I I I T d e v III_{T^{dev}} IIITdev是不变量,所以 cos 3 θ \cos 3\theta cos3θ也是不变量
参考教材:
Eduardo W.V. Chaves, Notes On Continuum Mechanics