1.算法描述

灰狼优化算法(GWO),灵感来自于灰狼.GWO算法模拟了自然界灰狼的领导层级和狩猎机制.四种类型的灰狼,如 α,β,δ,w 被用来模拟领导阶层。此外，还实现了狩猎的三个主要步骤:寻找猎物、包围猎物和攻击猎物。

为了在设计GWO算法时对灰狼的社会等级进行数学建模,我们将最适解作为α .因此,第二和第三个最佳解决方案分别被命名为 β 和 δ .剩下的候选解被假定为 w .在GWO算法中,狩猎过程由，α，β 和 δ 引导. w 狼跟随这三只狼。

在狩猎过程中，将灰狼围捕猎物的行为定义如下：

D=|C⋅Xp(t)−X(t)| (1)

X(t+1)=Xp(t)−A⋅D (2)

式(1)表示个体与猎物间的距离,式(2)是灰狼的位置更新公式.其中, t 是目前的迭代代数， A 和 C 是系数向量, Xp 和 X 分别是猎物的位置向量和灰狼的位置向量. A 和 C 的公式如下：

A=2a⋅r1−a (3)

C=2⋅r2 (4)

其中, a 是收敛因子,随着迭代次数从2线性减小到０, r1 和 r2 的模取[0,1]之间的随机数.

2.2 狩猎

灰狼能够识别猎物的位置并包围它们.当灰狼识别出猎物的位置后, β 和 δ 在 α 的带领下指导狼群包围猎物.灰狼个体跟踪猎物位置的数学模型描述如下：

Dα=|C1⋅Xα−X|

Dβ=|C2⋅Xβ−X| (5)

Dδ=|C3⋅Xδ−X|

其中, Dα , Dβ和 Dδ 分别表示 α,β 和 δ 与其他个体间的距离; Xα,Xβ 和 Xδ 分别代表 α,β 和 δ 当前位置; C1,C2,C3 是随机向量, X 是当前灰狼的位置。

X1=Xα−A1⋅(Dα)

X2=Xβ−A2⋅(Dβ) (6)

X3=Xδ−A3⋅(Dδ)

X(t+1)=X1+X2+X33 (7)

式(6)分别定义了狼群中 w 个体朝向 α,β 和 δ 前进的步长和方向,式(7)定义了ω的最终位置。

2.3 攻击猎物

当猎物停止移动时,灰狼通过攻击来完成狩猎过程.为了模拟逼近猎物, a 的值被逐渐减小,因此 A 的波动范围也随之减小.换句话说,在迭代过程中,当 a 的值从２线性下降到０时,其对应的 A 的值也在区间 [−a,a] 内变化.如图3所示,当 A 的值位于区间内时,灰狼的下一位置可以位于其当前位置和猎物位置之间的任意位置.当 |A|<1 时,狼群向猎物发起攻击(陷入局部最优).当 |A|>1 时,灰狼与猎物分离,希望找到更合适的猎物(全局最优).

GWO算法还有另一个组件 C 来帮助发现新的解决方案.由式(4)可知, C 是[0,2]之间的随机值. C 表示狼所在的位置对猎物影响的随机权重, C>1 表示影响权重大,反之,表示影响权重小.这有助于ＧＷＯ算法更随机地表现并支持探索,同时可在优化过程中避免陷入局部最优.另外,与 A 不同, C 是非线性减小的.这样,从最初的迭代到最终的迭代中,它都提供了决策空间中的全局搜索.在算法陷入了局部最优并且不易跳出时, C 的随机性在避免局部最优方面发挥了非常重要的作用,尤其是在最后需要获得全局最优解的迭代中.

2.仿真效果预览

matlab2022a仿真结果如下：

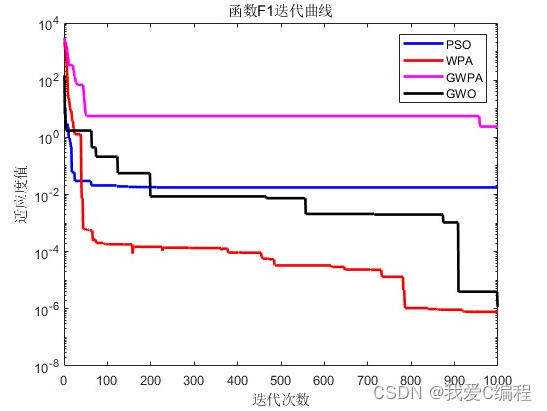
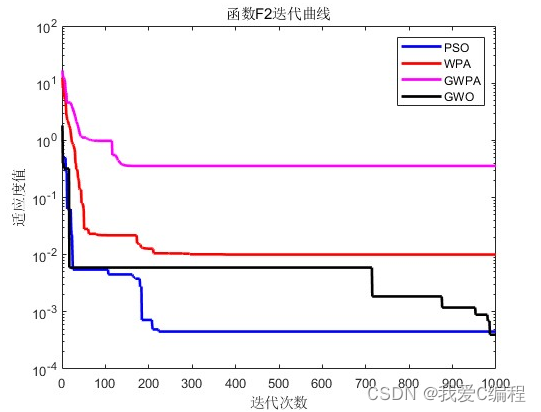
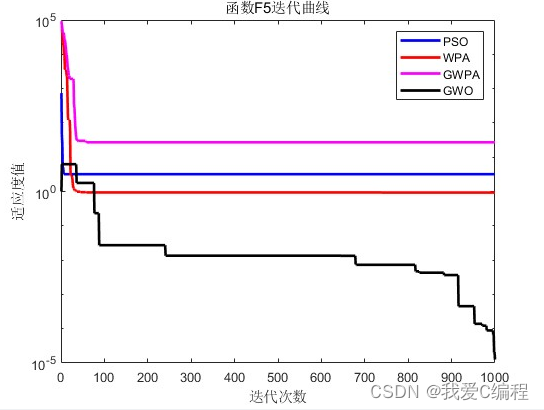
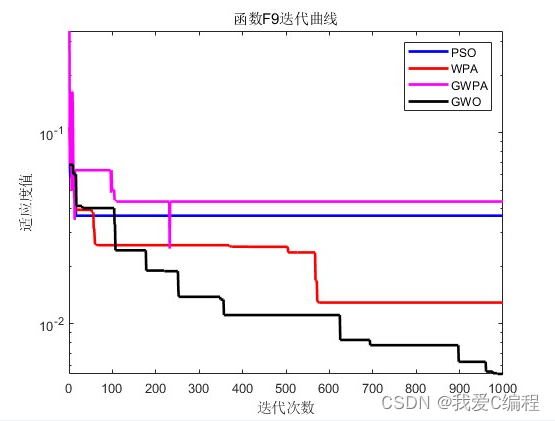
3.MATLAB核心程序

...........................................................
Iters = 1000;         %最大迭代次数
Num   = 50;           
%初始化种群的个体(可以在这里限定位置和速度的范围)
xpos  = Lmin + (Lmax-Lmin)*rand(Num,dim);
xpos0 = xpos;
Alpx  = zeros(1,dim);
Alps  = 1000;  
btx   = zeros(1,dim);
bts   = 1000;   
dltx  = zeros(1,dim);
dlts  = 1000; 
Pbest = zeros(1,Iters);
for t=1:Iterstfor i=1:Num    if t > 1r1      = rand; r2      = rand;A0      = 2*a*r1-a;%公式5C0      = 2*r2;    %公式6dd      = abs(C0*xpos(i,:)-xpos0(i,:));xpos(i,:) = xpos(i,:) - A0*dd;    endYi        = func_F1_10(xpos(i,:),sel); if Yi<Alps Alps = Yi; Alpx = xpos(i,:);endif Yi>Alps && Yi<bts bts = Yi; btx = xpos(i,:);endif Yi>Alps && Yi>bts && Yi<dlts dlts = Yi; dltx = xpos(i,:);endenda=2*(1-(t/Iters));  for i=1:Numfor j=1:dim       r1      = rand; r2      = rand;A1      = 2*a*r1-a;%公式5C1      = 2*r2;    %公式6D_alpha = abs(C1*Alpx(j)-xpos(i,j));%公式7X1      = Alpx(j)-A1*D_alpha;       %公式10r1      = rand; r2      = rand;A2      = 2*a*r1-a; %公式5C2      = 2*r2; %公式6D_beta  = abs(C2*btx(j)-xpos(i,j)); %公式8X2      = btx(j)-A2*D_beta; %公式11    r1      = rand; r2      = rand;A3      = 2*a*r1-a; %公式5C3      = 2*r2; %公式6D_delta = abs(C3*dltx(j)-xpos(i,j)); %公式9X3      = dltx(j)-A3*D_delta; %公式12           xpos(i,j) = (X1+X2+X3)/3;%公式13endendPbest(t) = func_F1_10(Alpx,sel); 
end
02_060m