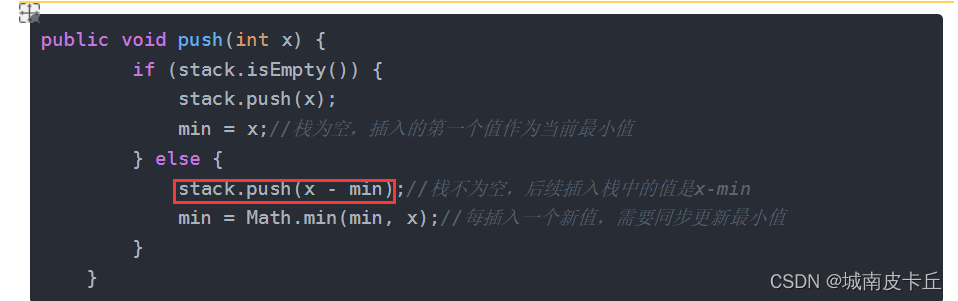
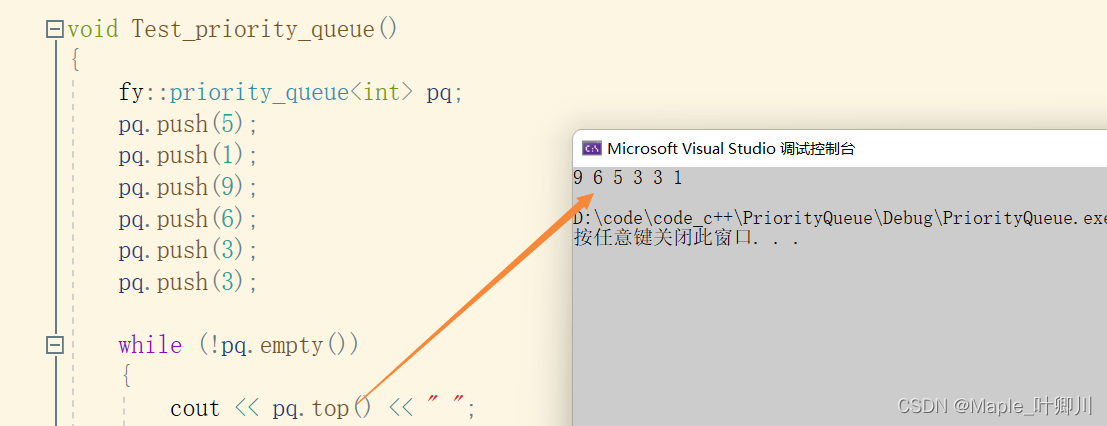
🚀🚀🚀大家觉不错的话,就恳求大家点点关注,点点小爱心,指点指点🚀🚀🚀
方阵的行列式
(1) |A^T|=|A|
(2) |𝛌A|=𝛌^n|A|
(3) |AB|=|A||B|
(4) |AB|=|BA|
伴随矩阵:A*=A^T

A*(A*)=(A*)*A=|A|E
逆矩阵:
定义7:对于n阶矩阵A,如果有一个n阶矩阵B,使
AB=BA=E
则说明矩阵A是可逆的,并把矩阵B称为矩阵A的逆矩阵
A的逆矩阵记作A^-1,AB=BA=E,则B=A^-1
定理1: 若矩阵A可逆,则|A|不等于0
定理2: A^-1=(1/|A|)A*
推论:(1)若A可逆,则A^-1也是可逆,且
(A^-1)^-1=A
(2)若A,B为同阶矩阵且均可逆,则AB也是可逆的,且
(AB)^-1=(B^-1)(A^-1)
克拉默法则
(1)如果线性方程组的系数矩阵A的行列不等于0,那么方程组有唯一的解
矩阵分块(用的很少)
第三章
矩阵的初等变换与线性方程组
定义1:下面三种变换称为初等行变换
(1)对换两行(对换i,j两行,记作r[i]<->r[j])
(2)以数k(k不等于0)乘某一行中的所有元素(第i行乘k,记作r[i]xk)
(3)把某一行所有元素的k倍加到另一行对应的元素上去(第j行的k倍加到第i行上,记作r[i]+kr[j])
初等列变换,把初等行变换中的‘行’换成’列’
注意:矩阵是增广矩阵
如果矩阵A经有限次初等行变换变成矩阵B,就称矩阵A与B行等价,记作A~B
(1)A~A
(2)A~B,则B~A
(3)
定义2:
行阶梯形:
(1)非零矩阵满足非零行在零行的上面;非零行的首非零元素所在列在上一行(如果存在的话)的首非零元素所在列的右面,则称矩阵为行阶梯形矩阵
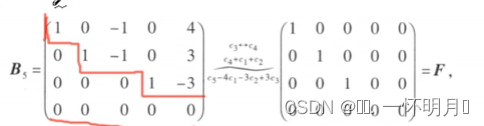
(2)行最简形:
非零行的首非零元素为1;首非零元素所在的列其他元素为零,则称为行最简形矩阵
利用初等行变换求逆矩阵

🌸🌸🌸如果大家还有不懂或者建议都可以发在评论区,我们共同探讨,共同学习,共同进步。谢谢大家! 🌸🌸🌸