目录

一、前言

二、是什么？

三、为什么？

四、怎么看？ 

五、干什么？

---

一、前言

 这是什么东东？史密斯圆图能干啥用？

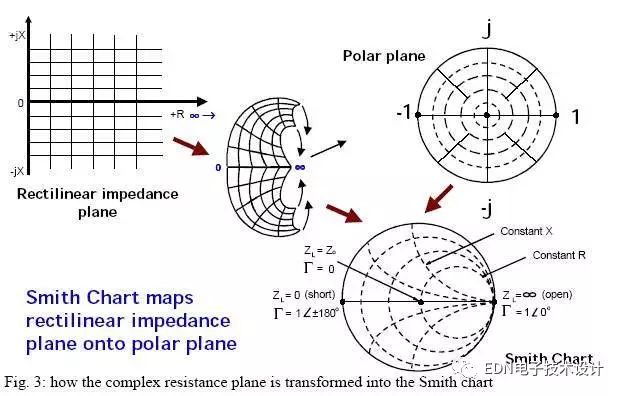
二、是什么？

史密斯圆图，就是做高频电路之间的阻抗匹配用的。

该图表是由菲利普·史密斯(Phillip Smith)于1939年发明的，当时他在美国的RCA公司工作。史密斯曾说过，“在我能够使用计算尺的时候，我对以图表方式来表达数学上的关联很有兴趣”。

史密斯图表的基本在于以下的算式。

当中的Γ代表其线路的反射系数(reflection coefficient)

即S参数（S-parameter）里的S11，ZL是归一负载值，即ZL / Z0。当中，ZL是线路本身的负载值，Z0是传输线的特征阻抗（本征阻抗）值，通常会使用50Ω。

简单的说：就是类似于数学用表一样，通过查找，知道反射系数的数值。

三、为什么？

我们现在也不知道，史密斯先生是怎么想到“史密斯圆图”表示方法的灵感，是怎么来的。

很多同学看史密斯原图，死记硬背，不得要领，其实没有揣摩，史密斯老先生的创作意图。

我个人揣测：是不是受到黎曼几何的启发，把一个平面的坐标系，给“掰”了。

世界地图，其实是一个用平面表示球体的过程，这个过程是一个“掰直”。

史密斯原图，巧妙之处，在于用一个圆形表示一个无穷大的平面。

首先，我们先理解“无穷大”的平面。我们复习一下理想的电阻、电容、电感的阻抗。

在具有电阻、电感和电容的电路里，对电路中的电流所起的阻碍作用叫做阻抗。阻抗常用Z表示，是一个复数，实际称为电阻，虚称为电抗，其中电容在电路中对交流电所起的阻碍作用称为容抗 ,电感在电路中对交流电所起的阻碍作用称为感抗，电容和电感在电路中对交流电引起的阻碍作用总称为电抗。 阻抗的单位是欧姆。

R电阻：在同一电路中，通过某一导体的电流跟这段导体两端的电压成正比，跟这段导体的电阻成反比,这就是欧姆定律。

标准式： 

（理想的电阻就是 实数，不涉及复数的概念）。

如果引入数学中复数的概念，就可以将电阻、电感、电容用相同的形式复阻抗来表示。既：电阻仍然是实数R（复阻抗的实部），电容、电感用虚数表示，分别为：

Z= R+i( ωL–1/（ωC）)

说明：负载是电阻、电感的感抗、电容的容抗三种类型的复物，复合后统称“阻抗”，写成数学公式即是：阻抗Z= R+i(ωL–1/（ωC）)。其中R为电阻，ωL为感抗，1/（ωC）为容抗。

（1）如果(ωL–1/ωC) > 0，称为“感性负载”；

（2）反之，如果(ωL–1/ωC) < 0称为“容性负载”。

我们仔细看阻抗公式，它不再是一个实数。它因为电容、电感的存在，它变成了一个复数。

电路中如果只有电阻，只影响幅度变化。

我们通过上图，我们知道，正弦波的幅度发生了变化，同时，相位也发生了变化，同时频率特性也会变化。所以我们在计算的过程中，即需要考虑实部，也需要考虑虚部。

我们可以在一个复平面里面，以实部为x轴、以虚部为y轴，表示任意一个复数。我们的阻抗，不管多少电阻、电容、电感串联、并联，之后，都可以表示在一个复平面里面。

 任意一个阻抗的计算结果，我们都可以放在这个复平面的对应位置。各种阻抗的情况，组成了这个无穷大的平面。

掰弯

在复平面中，有三个点，反射系数都为1，就是横坐标的无穷大，纵坐标的正负无穷大。历史上的某天，史密斯老先生，如有神助，把黑色线掰弯了，把上图中，三个红色圈标注的点，捏到一起。

弯了，弯了

圆了，圆了

完美的圆

黑色的线上的阻抗，有个特点：实部为0；（电阻为0）

红色的线上的阻抗，有个特点：虚部为0；（电感、电容为0）

绿色的线上的阻抗，有个特点：实部为1；（电阻为50欧姆）

紫色的线上的阻抗，有个特点：虚部为-1；

蓝色的线上的阻抗，有个特点：虚部为1；

四、怎么看？ 

简而言之，是看一线、两弧和两圆、三点。

接下来我们就从一线和三点讲起

 

史密斯圆图被一条名为电阻线的蓝色横线分成上下两个半区，上半部分叫电感区，那里所有点的虚部值部为正。下半部分叫电容区，那里所有点的虚部值部为负。而电阻线本身的虚部阻抗值不正不负，他上面每一个点的阻抗值均为0Ω，所以电阻线是一条特殊的实部线。电阻线上有三个点，最左侧的叫短路点，它表示实部值为0Ω，虚部值也为0Ω的情况；最右侧的叫断路点，他表示实部值为无穷大，虚部值也为0Ω的情况；而中间点，也就是圆心那是匹配点，那里的阻值是标准阴值，一般情况下他是50Ω，三点是史密斯圆图的基点，也是我们校正天线分析仪的起点。

两圆两弧——等实部圆和等虚部弧

红色的圆圈都叫阻抗圆，而绿色的圆圈都叫导纳圆，我们在电阻线上找到实部阻抗值或者实部导纳值之后，就要沿着阻抗圆或者电纳圆去找虚部值。其中电阻线以上的点是正值，代表阻抗点的虚部值呈现感性。电阻线以下的点是负值，代表阻抗点的虚部值呈现容性（上感下容）

到底怎么读图？

先说归一化阻抗值的读图方法：

第一步，用阻抗值除以标准电阻，得到归一化实部阻抗值和归一化虚部阻抗值。

第二步，在等电阻线上，找到归一化实部阻抗值对应的阻抗圆。

第三步，沿着阻抗圆，向上或向下旋转，找与归一化虚部阻抗值对应的等电抗弧。

第四步，做个记号，就算OK。

举个例子

100Ω-j50Ω在哪儿？

第一步，计算归一化实部阻抗值为100Ω/50Ω=2；归一化虚部阻抗值为-50Ω/50Ω=-1。

第二步，在等电阻线上，找到归一化阻抗值为2的阻抗圆。

第三步，沿着归一化阻抗值为2的阻抗圆下旋，转到-1那个电抗弧上。

第四步，做个记号！我标的是X。

怎么查100Ω+j50Ω的点？

先找到100Ω阻抗圆，然后沿着它的轨迹上旋，到达虚部值为50Ω的地

方，然后做个标记，就是Y点。

归一化导纳值呢？

简单讲，导纳值坐标系和阻抗值的查法、标注方法完全一样。

举个例子

0.04S+j0.02S的点在哪儿？

第一步，计算归一化实部导纳值为0.04S/0.02S=2；归一化虚部导纳值为0.02S/0.02S=1。

第二步，在等电阻线上，找到归一化导纳值为2的导纳圆。

第三步，沿着归一化导纳值为2的导纳圆上旋，转到导纳值为1的那个电纳弧上。

第四步，做个记号！即Z。

怎么查0.04S-j0.02S的点？

先找到0.04S导纳圆，然后沿着它的轨迹下旋，到达虚部值为-0.02S的地方，然后做个标记，那就是S点。

五、干什么？

解释和介绍了史密斯圆图这么长的段落，别忘了，我们想干什么。我们实际是希望，我们设计的电路反射系数越接近0越好。但是，什么样的电路是合格的电路呢？反射系数不可能理想的为0，那么我们对反射系数，有什么样的要求呢？

我们希望反射系数的绝对值小于1/3，即反射系数落入史密斯圆图的蓝色区域中（如下图）。

这个蓝色的球，有什么特色呢？其实我们通过史密斯原图的数值已经清楚的发现。在中轴线，也就是之前说的红线上，分别是25欧姆，和100欧姆两个位置。即在1/2 Zo和2倍Zo之间的区域。也就是，我们打靶打在蓝色区域，即认为反射系数是可以接受的。 

请看下图，图上这些棕色圆圈是等VSWR圆，也就是等驻波比圆。这个驻波比圆的特点是越靠近圆 心，驻波比越小，比如圆心那点是1，也就是说输入端送出进去多少信号，负截端就吸收多少信 号能量一点没糟蹋。驻波比为1.5，意味着有4％的功率撞到输出端又撞回输入端了。驻波比2，就意味着有11％的能量撞回去了。通常来说，小信号阻抗匹配电路对驻波比要求比较低达到，达到1.5就算良好匹配了。如果体积有限制，还可以进一步放宽一些。但是如果是强信号，电台天线那种场合，SWR控制的就比较严格了，大功率电台，通信基站要控制在1.2以内。