A - Long Shuffle
这道题本质是一个找规律的题
既然是打表题,我们先暴力把他打出来

(盗一张图.jpg)
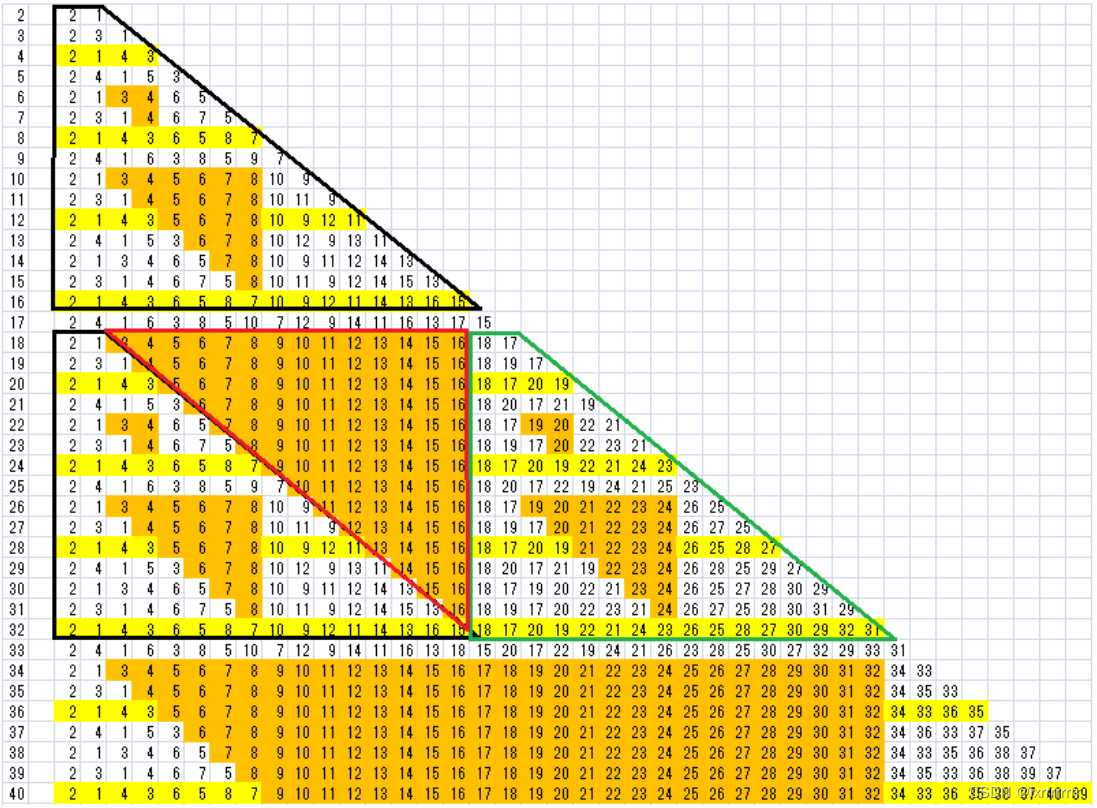
接下来就是在这张图中挖掘答案
我们可以明显的看到偶数行是有一些规律的
要么是相邻对的互换,要么不变
不变和互换的位置也有讲究,在二进制下可以发现这样的规律

这里的n和k代表第n行的第k个数
我们发现偶数行完全满足这个公式
而对于奇数行,看起来没什么规律
我们可以联系n-1行,也就是奇数行对应的上一个偶数行
可以发现对于奇数行A(i,j),满足A(i,j)=A(i-1,A(i-1,j-1)+1) 当j大于1且小于n
代码如下:
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fer(i,a,b) for(int i=a;i<=b;++i)
#define der(i,a,b) for(int i=a;i>=b;--i)
#define all(x) (x).begin(),(x).end()
#define pll pair<int,int>
#define et cout<<'\n'
#define xx first
#define yy second
using namespace std;
int A[105];
void go(int l, int r) {if (l + 1 == r) {swap(A[l], A[r]);}else {go(l, r - 1);go(l + 1, r);}
}//暴力
int back(int n, int k) {k--;int block = k / 2;int F = n / 2 - 1;if ((F & block) == block) {k ^= 1;}return k + 1;
}
signed main() {ios_base::sync_with_stdio(false);cin.tie(0);int tst;cin >> tst;while (tst--) {int n, k;cin >> n >> k;if (n % 2 == 1) {if (k > 1) {k = back(n - 1, k - 1);k++;}if (k <= n - 1) {k = back(n - 1, k);}cout << k << '\n';}else {int f1 = back(n, k);cout << f1 << '\n';}}return 0;
}B - Summation By Construction
这道题就很玄学
除了2是NO,其他都是YES
其中一种解决方式是
我们可以用对角线的思路来构建
比如
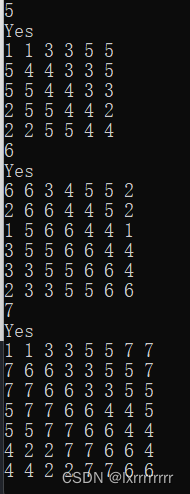
代码如下
#include <bits/stdc++.h>
#define int long long
#define pb push_back
#define fer(i,a,b) for(int i=a;i<=b;++i)
#define der(i,a,b) for(int i=a;i>=b;--i)
#define all(x) (x).begin(),(x).end()
#define pll pair<int,int>
#define et cout<<'\n'
#define xx first
#define yy second
using namespace std;
constexpr int max_n=100;
int a[max_n+1][max_n+2];
void test(){int n;cin>>n;if(n==2){puts("No");return;}puts("Yes");if((n&1)){int m=n+1;for(int i=1; i<=n; i+=2){int now=i;for(int j=1; j<=n; ++j){int col=j<=i?i:(n-i);a[j][now]=col;++now>m&&(now=1);a[j][now]=col;}}for(int i=1; i<=n; ++i){for(int j=1; j<=n; ++j)cout<<a[i][j]<<" ";cout<<a[i][m]<<'\n';}return;}const int m=n+1;for(int i=1; i<=n; ++i)a[i][i]=a[i][i+1]=n;for(int j=2; j<=n; ++j)a[j%n+1][j]=a[(j+1)%n+1][j]=n-1;a[2][1]=a[n][1]=a[2][m]=a[1][m]=2;a[3][1]=a[3][m]=1;for(int i=3,ed=n-3; i<=ed; i+=2){int now=i+1;for(int j=1; j<=m; ++j){const int col=j<=i?i:(m-i);a[now][j]=col;++now>n&&(now=1);a[now][j]=col;}}for(int i=1; i<=n; ++i){for(int j=1; j<=n; ++j)cout<<a[i][j]<<" ";cout<<a[i][m]<<'\n';}
}
signed main(){int t;cin>>t;while(t--){test();}return 0;
}


![[ 常用工具篇 ] CobaltStrike(CS神器)基础(一) -- 安装及设置监听器详解](https://img-blog.csdnimg.cn/6ad497c5c195459b8cfdd024c4400c52.png)