🔥Go for it!🔥
📝个人主页:按键难防
📫 如果文章知识点有错误的地方,请指正!和大家一起学习,一起进步👀📖系列专栏:数据结构与算法
🔥 如果感觉博主的文章还不错的话,还请 点赞👍🏻收藏⭐️ + 留言📝支持 一下博主哦
目录
栈:
顺序存储实现栈:
判断栈是否为空:
入栈操作:
出栈(弹栈)操作:
读取栈顶元素:
汇总:
队列:
循环队列(数组实现):
定义方法:
循环队列入队:
循环队列出队:
汇总:
链式存储实现队列:
定义方法:
初始化头尾指针:
入队:
出队:
汇总:
栈:
栈(stack)是一个特殊的线性表,是限定仅在一端(通常是表尾)进行插入和删除操作的线性表。又称为后进先出(Last In First Out)的线性表,简称 LIFO 结构。
特点:
后进先出,先进者后出。
顺序存储实现栈:
#define MaxSize 50 //定义栈的长度
typedef int ElemType;//重定义栈中每个元素的类型,便于修改
typedef struct{ElemType data[MaxSize];//数组int top;//始终指向栈顶的一个变量
}SqStack;
SqStack S;
栈顶(Top):线性表允许进行插入删除的那一端。
栈底(Bottom):固定的,不允许进行插入和删除的另一端。
空栈:不含任何元素的空表。
基本操作:
判断栈是否为空:
void InitStack(SqStack &S)//初始化栈
{S.top = -1;//让栈为空就是初始化栈
}
bool StackEmpty(SqStack &S)//验证是否初始化成功
{if (S.top == -1){return true;}else{return false;}
}入栈操作:
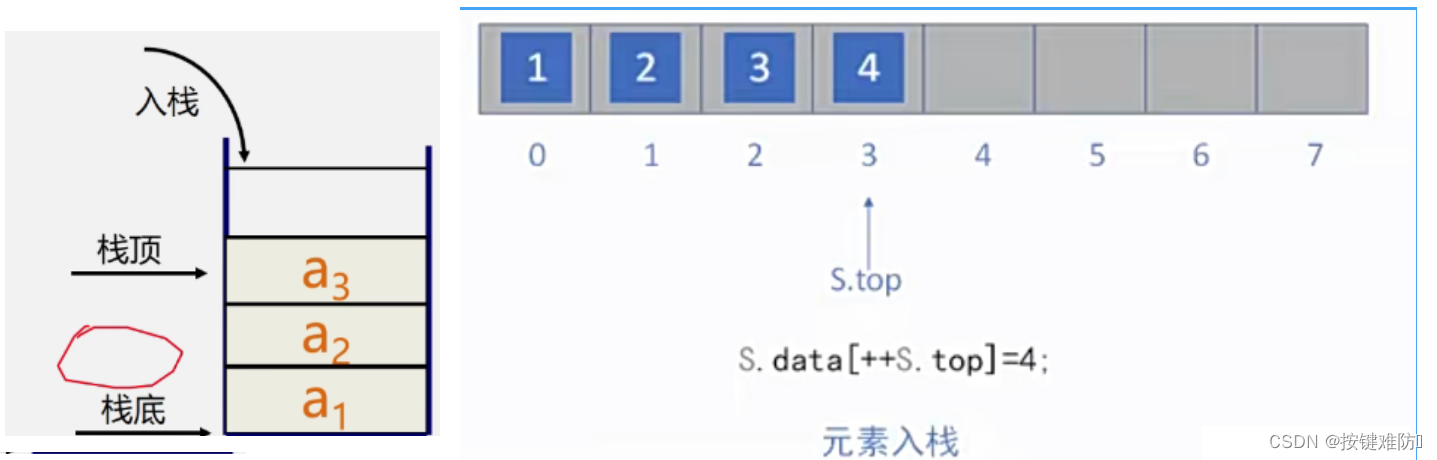
前置++,既实现先扩容,又解决了元素入栈。
//入栈
bool Push(SqStack &S, ElemType x)
{if (S.top == MaxSize - 1)//数组的大小不能改变,避免访问越界{return false;}S.data[++S.top] = x;{return true;}
}出栈(弹栈)操作:
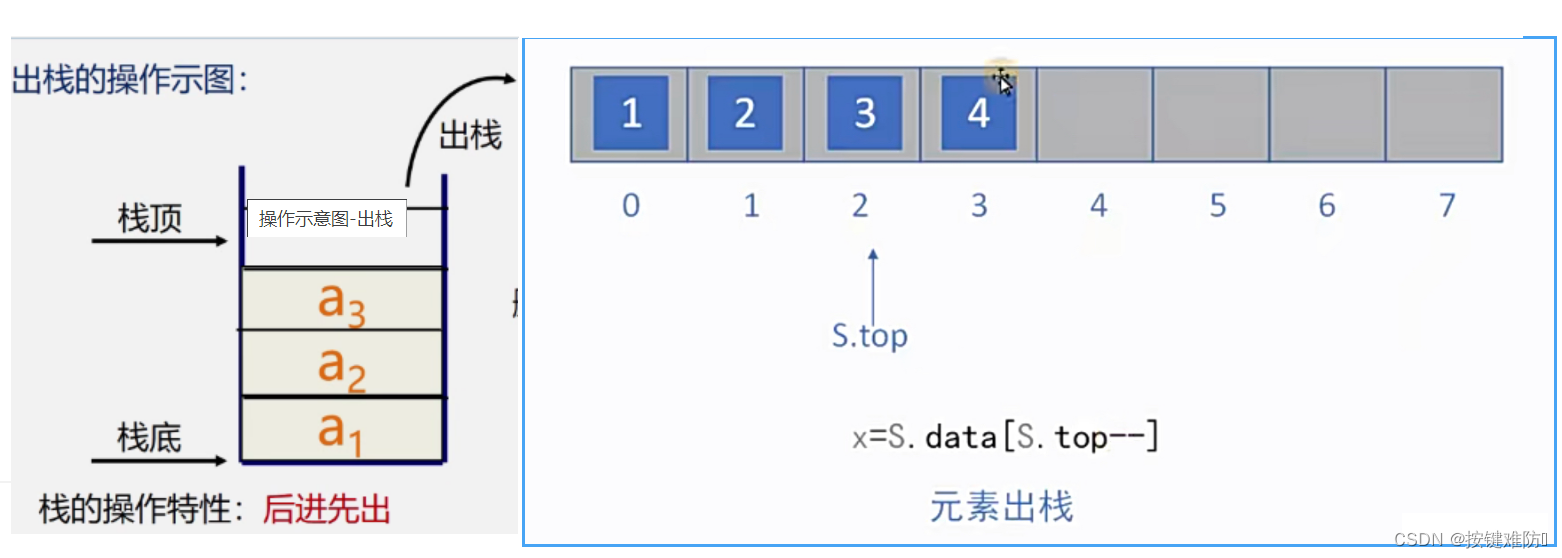
后置--,先元素出栈,后减容。
//弹出栈顶元素(出栈)
bool Pop(SqStack &S, ElemType &x)
{if (-1 == S.top)return false;x = S.data[S.top--];//后减减,x=S.data[S.top];S.top=S.top-1;{return true; }
}读取栈顶元素:
//读取栈顶元素
bool GetTop(SqStack &S, ElemType &x)
{if (-1 == S.top)//说明栈为空{return false;}x = S.data[S.top];{return true;}
}汇总:
初始化栈,判断栈是否为空,压栈,获取栈顶元素,弹栈。注意 S.top 为-1 时,代表栈为空。
#include <stdio.h>
#include <stdlib.h>
#define MaxSize 50
typedef int ElemType;
typedef struct{ElemType data[MaxSize];//数组int top;
}SqStack;
void InitStack(SqStack &S)
{S.top = -1;//代表栈为空
}
bool StackEmpty(SqStack &S)
{if (S.top == -1){return true;}else{return false;}
}
//入栈
bool Push(SqStack &S, ElemType x)
{if (S.top == MaxSize - 1)//数组的大小不能改变,避免访问越界{return false;}S.data[++S.top] = x;{return true;}
}
//读取栈顶元素
bool GetTop(SqStack &S, ElemType &x)
{if (-1 == S.top)//说明栈为空{return false;}x = S.data[S.top];{return true;}
}
//弹出栈顶元素(出栈)
bool Pop(SqStack &S, ElemType &x)
{if (-1 == S.top)return false;x = S.data[S.top--];//后减减,x=S.data[S.top];S.top=S.top-1;{return true; }
}
//实现栈 可以用数组,也可以用链表,我们这里使用数组
int main()
{SqStack S;//先进后出 FILO LIFObool flag;ElemType m;//用来存放拿出的元素InitStack(S);//初始化flag = StackEmpty(S);//验证是否初始化成功if (flag){printf("栈是空的\n");}Push(S, 3);//入栈元素 3Push(S, 4);//入栈元素 4Push(S, 5);flag = GetTop(S, m);//获取栈顶元素if (flag){printf("获取栈顶元素为 %d\n", m);}flag = Pop(S, m);//弹出栈顶元素(出栈)if (flag){printf("弹出元素为 %d\n", m);}return 0;
}队列:
队列(Queue)简称队,也是一种操作受限的线性表,只允许在表的一端进行插入,而在表的另一端进行删除。向队列中插入元素称为入队或进队;删除元素称为出队或离队。
特点:
先进先出。
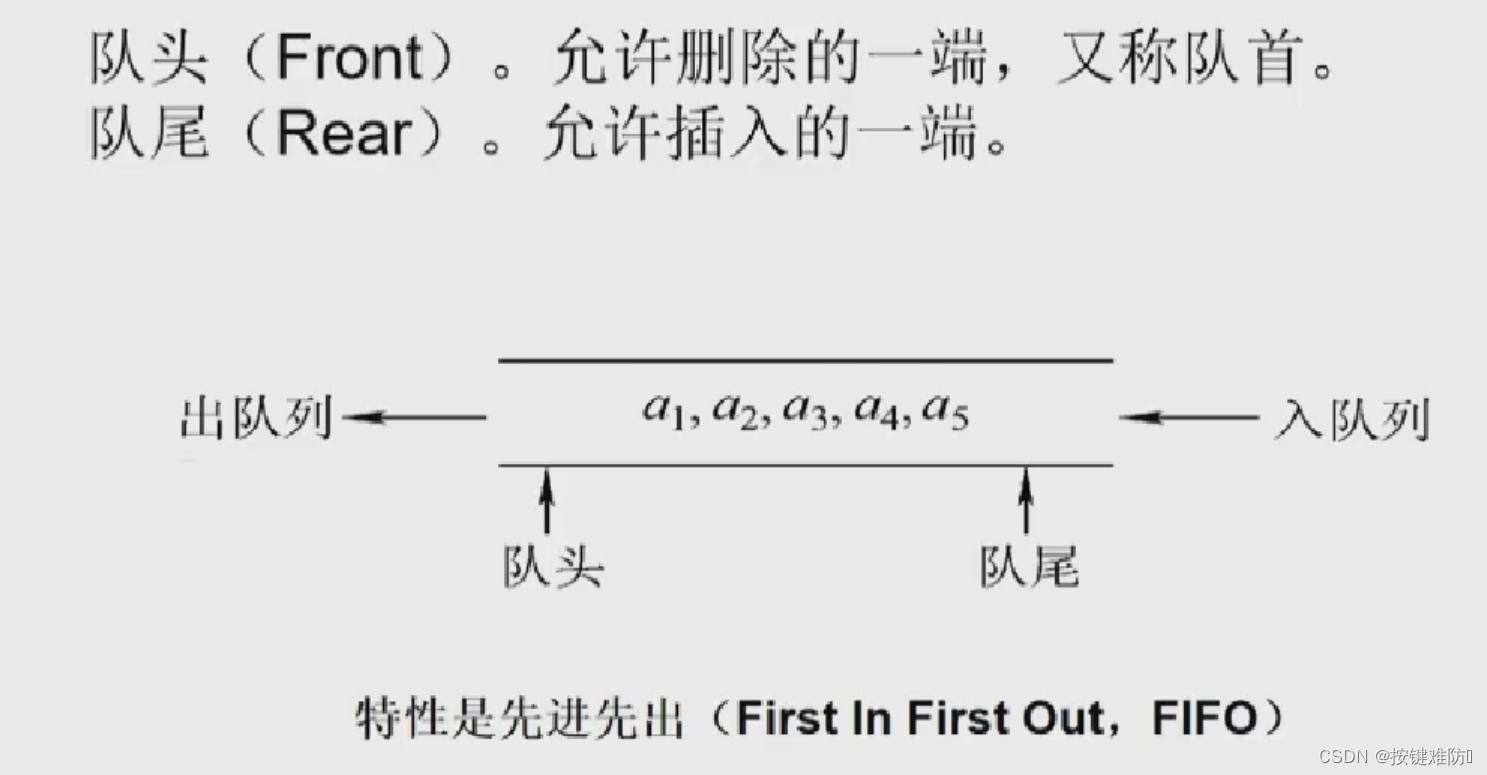
循环队列(数组实现):

定义方法:
#define MaxSize 5
typedef int ElemType;
typedef struct{ElemType data[MaxSize];//数组,存储MaxSize-1个元素int front, rear;//队列头 队列尾
}SqQueue;
SqQueue Q;front和rear都是下标
判断队列为空:front和rear指向同一个单元,且都是0
Q.front==Q.rear
判断队列满:front和rear中间空一个单元
(Q.rear+1)%MaxSize==Q.front
Q.rear+1为容量,如果%MaxSize=0(Q.front),那么队列满循环队列入队:
bool EnQueue(SqQueue &Q, ElemType x)
{if ((Q.rear + 1) % MaxSize == Q.front) //判断是否队满return false;Q.data[Q.rear] = x;//放入元素Q.rear = (Q.rear + 1) % MaxSize;//改变队尾标记,% MaxSize防止超出容量return true;
}循环队列出队:
bool DeQueue(SqQueue &Q, ElemType &x)
{if (Q.rear == Q.front)//判断是否队为空return false;x = Q.data[Q.front];//先进先出Q.front = (Q.front + 1) % MaxSize;//改变队头标记,% MaxSize防止超出容量return true;
}汇总:
#include <stdio.h>
#include <stdlib.h>
#define MaxSize 5
typedef int ElemType;
typedef struct{ElemType data[MaxSize];//数组,存储 MaxSize-1 个元素int front, rear;//队列头 队列尾
}SqQueue;
void InitQueue(SqQueue &Q)
{Q.rear = Q.front = 0;
}
//判空
bool isEmpty(SqQueue &Q)
{if (Q.rear == Q.front)//不需要为零{return true;}else{return false;}
}
//入队
bool EnQueue(SqQueue &Q, ElemType x)
{if ((Q.rear + 1) % MaxSize == Q.front) //判断是否队满{return false;}Q.data[Q.rear] = x;//3 4 5 6Q.rear = (Q.rear + 1) % MaxSize;{return true;}
}
//出队
bool DeQueue(SqQueue &Q, ElemType &x)
{if (Q.rear == Q.front){return false;}x = Q.data[Q.front];//先进先出Q.front = (Q.front + 1) % MaxSize;{return true;}
}
int main()
{SqQueue Q;bool ret;//存储返回值ElemType element;//存储出队元素InitQueue(Q);ret = isEmpty(Q);if (ret){printf("队列为空\n");}else{printf("队列不为空\n");}EnQueue(Q, 3);EnQueue(Q, 4);EnQueue(Q, 5);ret = EnQueue(Q, 6);ret = EnQueue(Q, 7);if (ret){printf("入队成功\n");}else{printf("入队失败\n");}ret = DeQueue(Q, element);if (ret){printf("出队成功,元素值为 %d\n", element);}else{printf("出队失败\n");}ret = DeQueue(Q, element);if (ret){printf("出队成功,元素值为 %d\n", element);}else{printf("出队失败\n");}ret = EnQueue(Q, 8);if (ret){printf("入队成功\n");}else{printf("入队失败\n");}return 0;
}链式存储实现队列:
定义方法:
typedef int ElemType;
typedef struct LinkNode
{//创建结点ElemType data;struct LinkNode *next;
}LinkNode;
typedef struct
{LinkNode *front, *rear;//结构体,用于存放队列头结点和队列尾结点的指针
}LinkQueue;//先进先出
LinkQueue Q;相对于原有编写的链表增加了尾指针
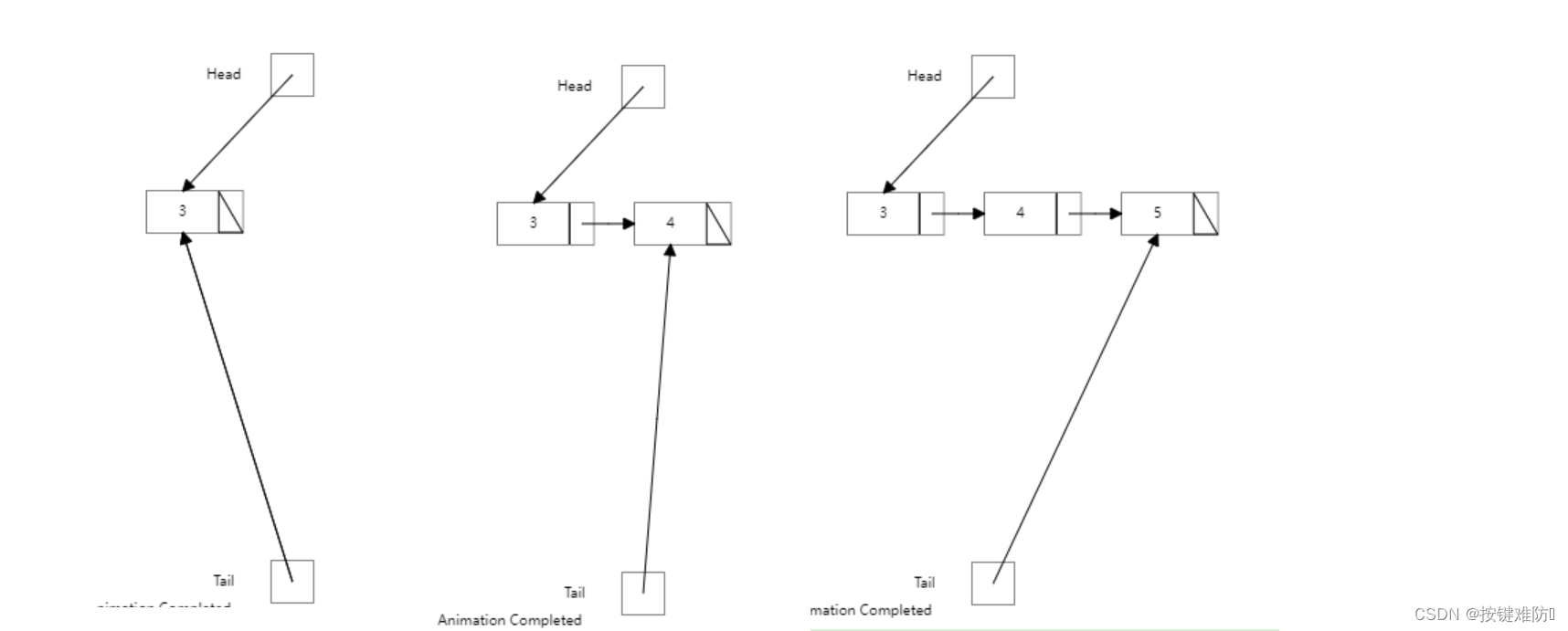
初始化头尾指针:
void InitQueue(LinkQueue &Q) //初始化头尾指针
{Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));//为头结点申请空间//初始化时头尾指针都指向这一头结点Q.front->next = NULL;//头结点的next指针为 NULL
}
bool IsEmpty(LinkQueue Q)
{if (Q.front == Q.rear)return true;elsereturn false;
}入队:
用链表的尾插法进行入队
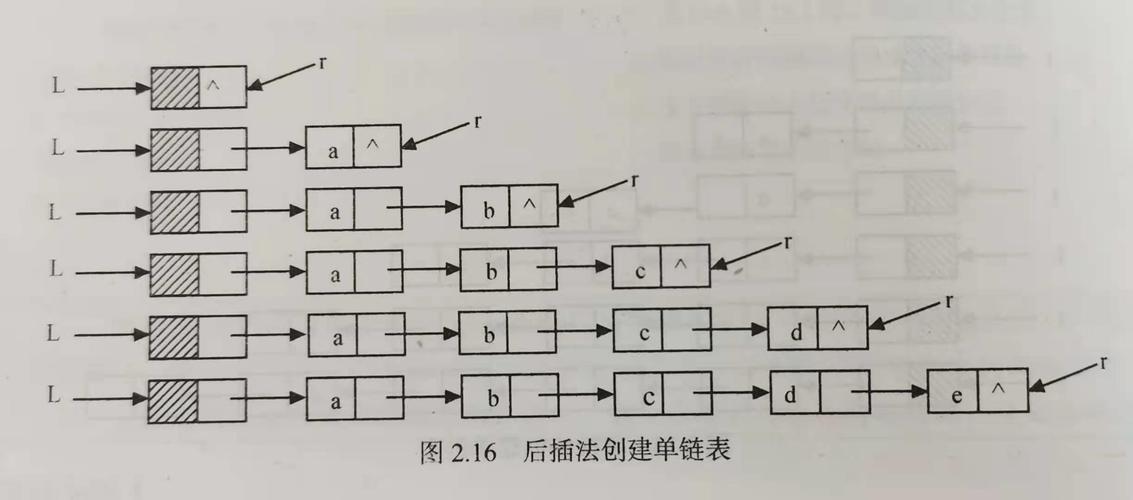
//入队,尾部插入法
void EnQueue(LinkQueue &Q, ElemType x)
{LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间s->data = x; s->next = NULL;//新申请的结点作为最后一个结点Q.rear->next = s;//先让前一结点(Q.rear)的指针域指向新插入的结点Q.rear = s;//然后再让Q.rear变为指向尾部的那个结点
}出队:
头部删除法,删除第一个节点,参数Q,用于删除操作的首尾指针结构体,x用于存放删除的第一个节点的数据。
//出队
bool DeQueue(LinkQueue &Q, ElemType &x)
{if (Q.front == Q.rear) {return false;//队列为空}LinkNode *p = Q.front->next;//front始终指向头结点,但头结点什么都没存,所以头结点的下一个节点才有数据x = p->data;Q.front->next = p->next;//断链,保留第一个结点的指针域,让头节点指向第二个结点if (Q.rear == p)//如果这个队列没有第二个结点,也就是p->next为NULLQ.rear = Q.front;//那直接让队列置为空free(p);//销毁动态内存return true;
}汇总:
#include <stdio.h>
#include <stdlib.h>
typedef int ElemType;
typedef struct LinkNode{ElemType data;struct LinkNode *next;
}LinkNode;
typedef struct
{LinkNode *front, *rear;//结构体,用于存放链表头和链表尾的指针
}LinkQueue;//先进先出
void InitQueue(LinkQueue &Q) //初始化头尾指针
{Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));//为头结点申请空间//头尾指针都指向这一头结点Q.front->next = NULL;//头结点的next指针为 NULL
}
bool IsEmpty(LinkQueue Q)
{if (Q.front == Q.rear)return true;elsereturn false;
}
//入队,尾部插入法
void EnQueue(LinkQueue &Q, ElemType x)
{LinkNode *s = (LinkNode *)malloc(sizeof(LinkNode));//为入队的元素申请空间s->data = x; s->next = NULL;Q.rear->next = s;//rear 始终指向尾部Q.rear = s;
}
//出队 头部删除法
bool DeQueue(LinkQueue &Q, ElemType &x)
{if (Q.front == Q.rear) return false;//队列为空LinkNode *p = Q.front->next;//头结点什么都没存,所以头结点的下一个节点才有数据x = p->data;Q.front->next = p->next;//断链if (Q.rear == p)//删除的是最后一个元素Q.rear = Q.front;//队列置为空free(p);return true;
}
int main()
{LinkQueue Q;bool ret;ElemType element;//存储出队元素InitQueue(Q);//初始化队列EnQueue(Q, 3);EnQueue(Q, 4);EnQueue(Q, 5);EnQueue(Q, 6);EnQueue(Q, 7);ret = DeQueue(Q, element);if (ret){printf("出队成功,元素值为 %d\n", element);}else{printf("出队失败\n");}return 0;
}