从Lec20开始，就转战CS61B Spring 2019了，18后面全变成公开课了。
本章主要讲的是Binary Search Tree，是一种非常流行的数据结构，据说各大面试中都会出现。其中用到了超多的recursion思想。

Binary Search Trees

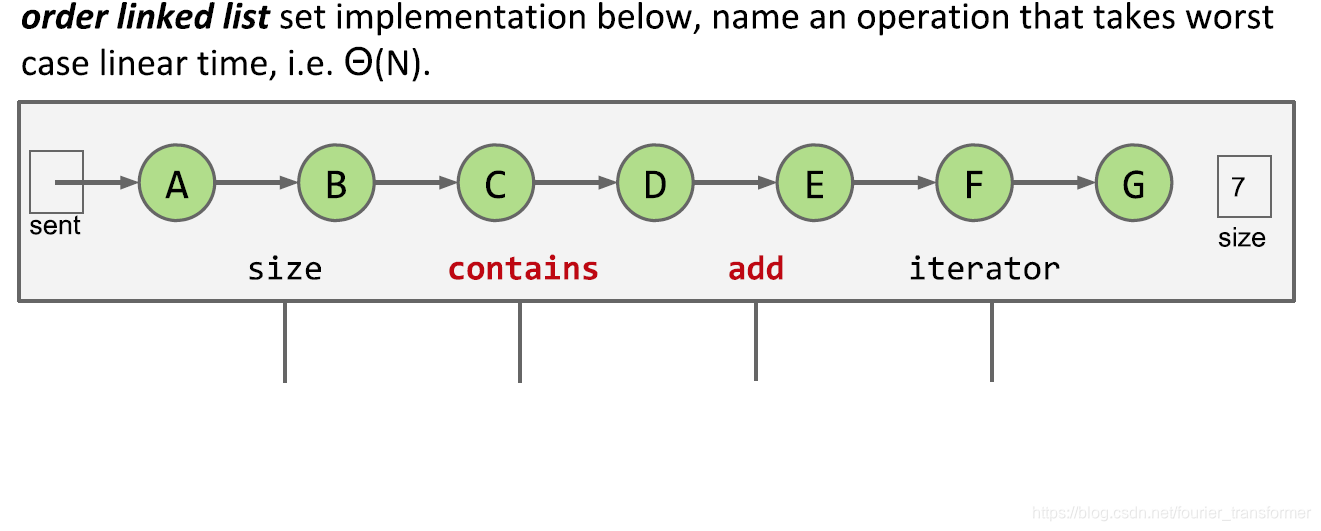
对于一个有序List，需要实现与查找有关的操作时，需要O(N)的复杂度，挺高的。怎么优化呢？
其实之前就想过这个问题。就像Deque结构一样，基本的思路是加入一些标记性的指针。

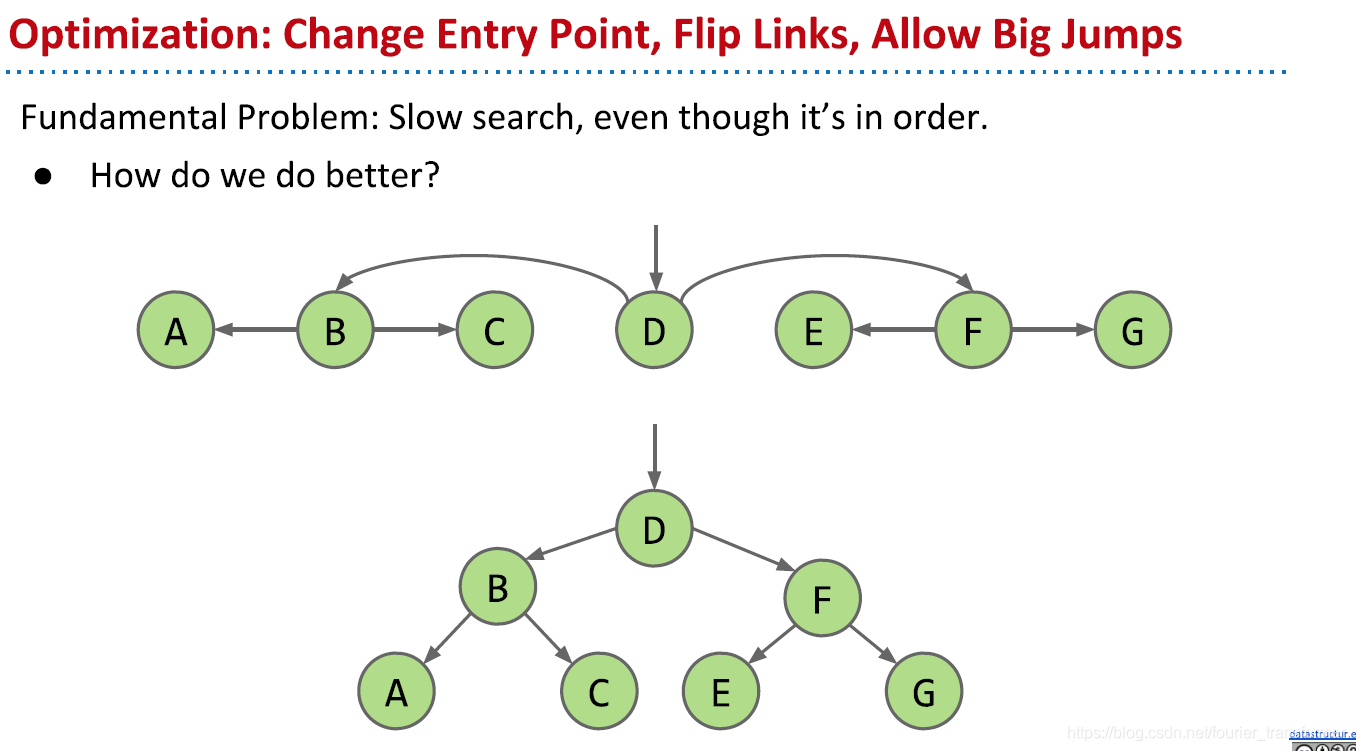
不断地在中间插入指针，并改变一些指针的方向，发现可以变为上图的树状结构，这就是一个基本二叉树。

二叉树的灵感来源还是二分查找算法。想到这我就有个问题：为什么会另外发明一个二叉树数据结构，而不是直接用二分法查找？

想了想，对于一组经常需要添加、删除操作的数据，需要查找 - 添加/删除 - 更新这三步。一个数组，查找一个值可以用二分法，复杂度跟二叉树一样，但是添加/删除复杂度就很高，拷过来拷过去的；一个链表，添加/删除很简单，但是查找就只能靠遍历。所以，综合以上两者的优势，才有了二叉树这种数据结构。

概念

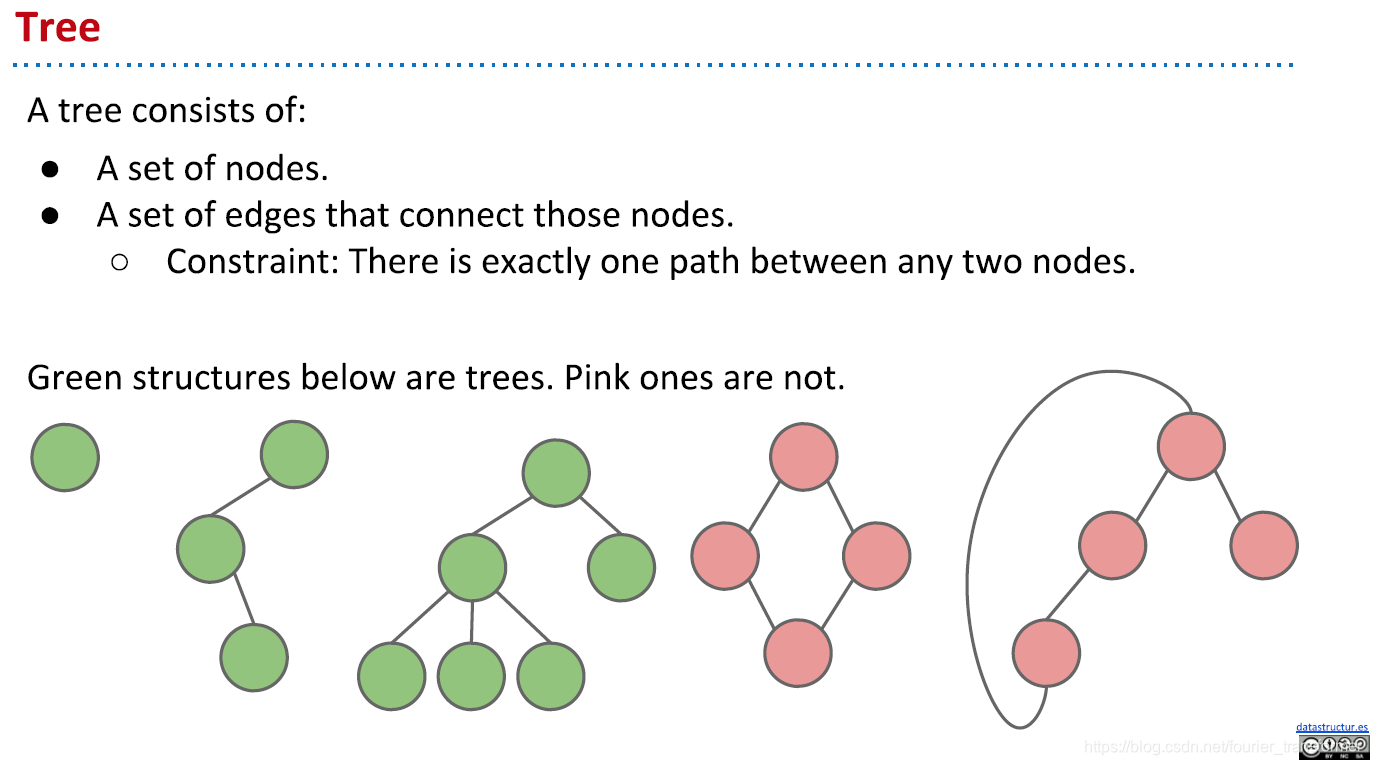
何为树？总结一句话就是：两个节点间只存在一条路。

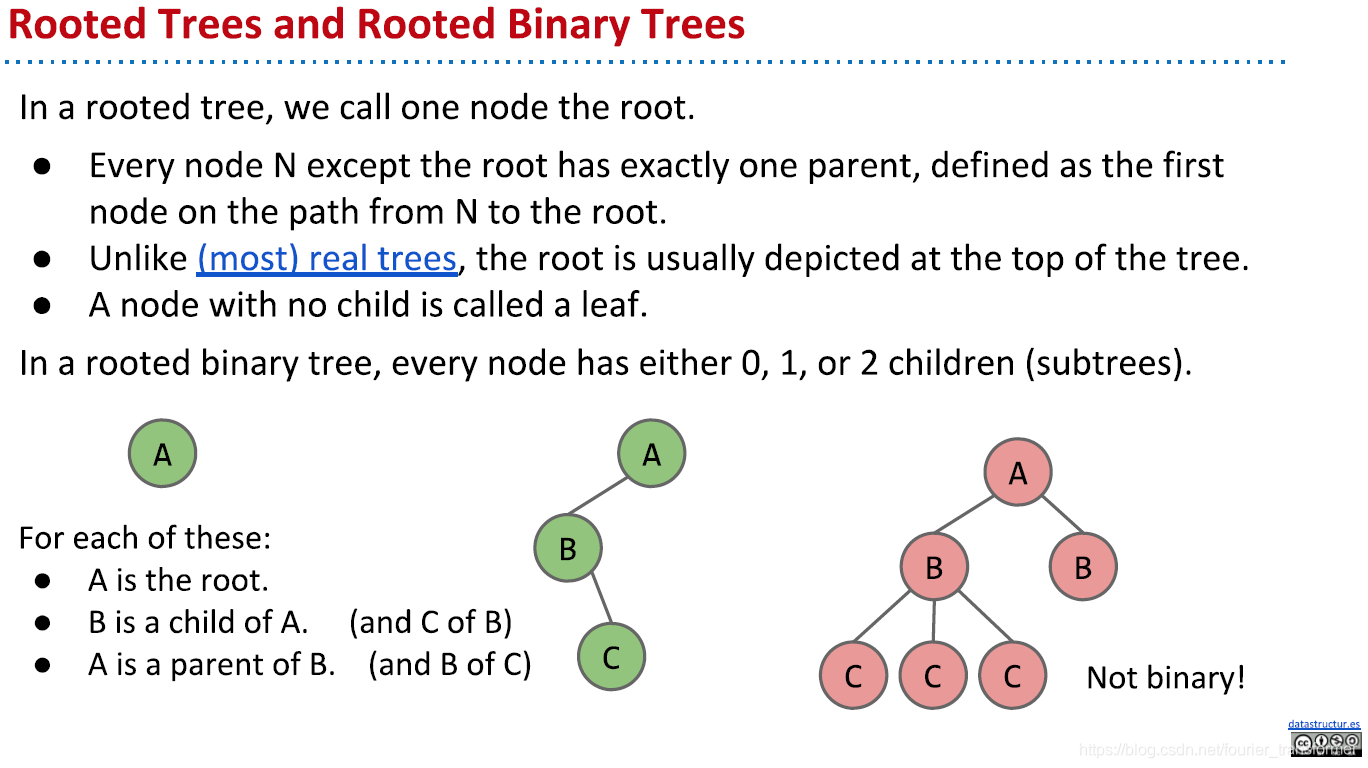
对于一个Binary Tree，每个节点只能有0~2个children，只能有1个parent。

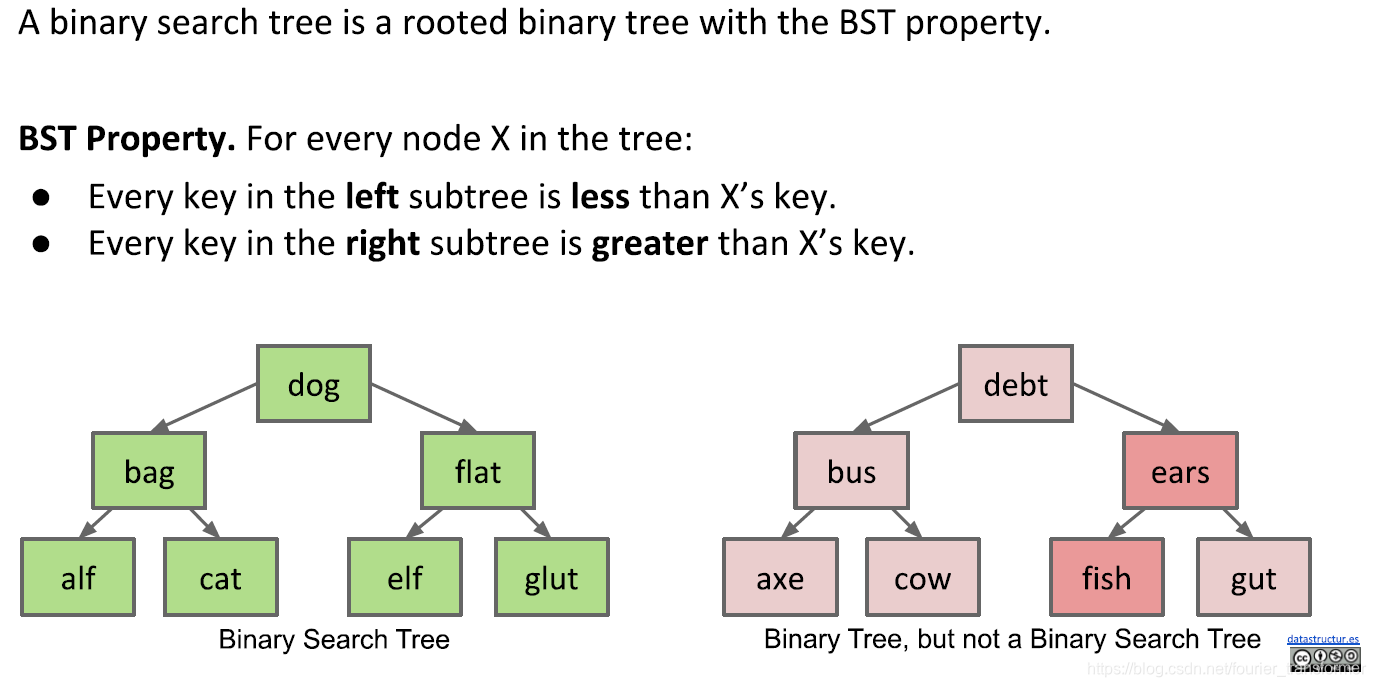
每个节点左边的子树上所有节点的值都小于该节点，右边子树上所有的值都大于该节点。
在思考二叉树的结构时，想着二分法查找一个数组就可以了，将二维的变成一维。

查找

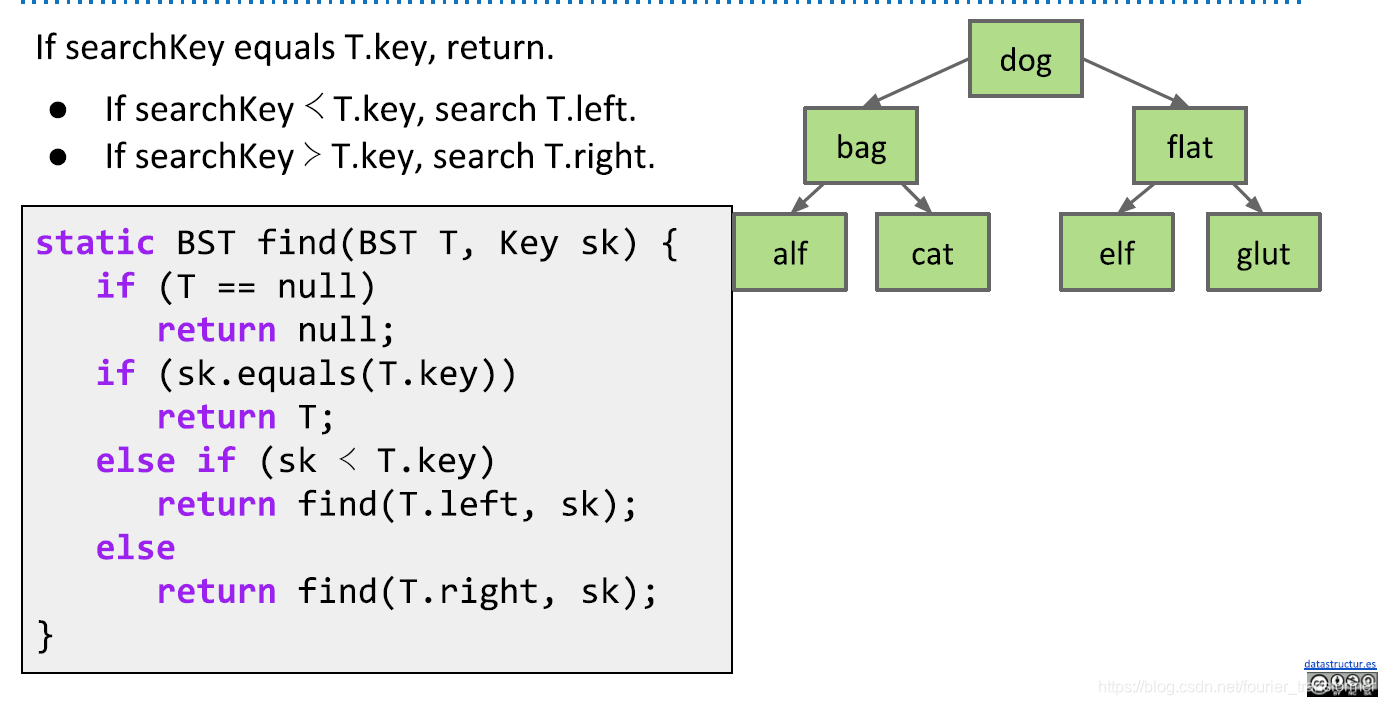
常规recursion，比较简单。复杂度为O(log(N))，与二分法一样。

插入

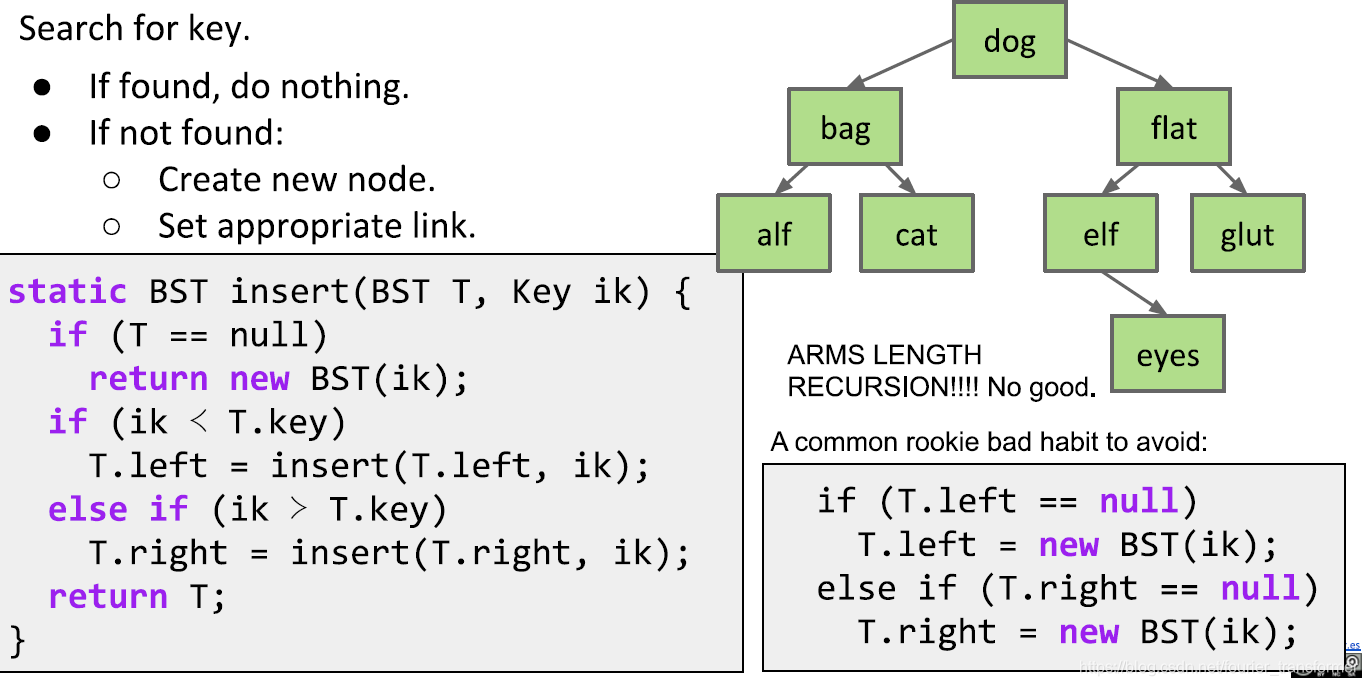
插入就十分巧妙了。如何插入呢？首先按照大小，在树中找插入的值，找到就不插了。没找到那肯定查到底了，到底了就按照树的规则，插左边或者右边。
然而实现的代码十分的recursive。第一个if，当插到底时返回一个新的节点。但是为什么只有返回没有指向？返回给谁？接下来一对if, else if解答了。如果找到了插入的父节点，会根据规则返回给T.left或者T.right；如果找到了和插入值相同的节点，则返回该节点，给上层的父节点的left或者right，没有任何改变。十分巧妙的recursion！
右边的代码是我们最容易想到的recursion的方式，一点都不优雅。

删除

最麻烦的是删除某个节点。插入肯定是插到底，删除就有三种可能：没有chiledren、有一个child和有两个children。

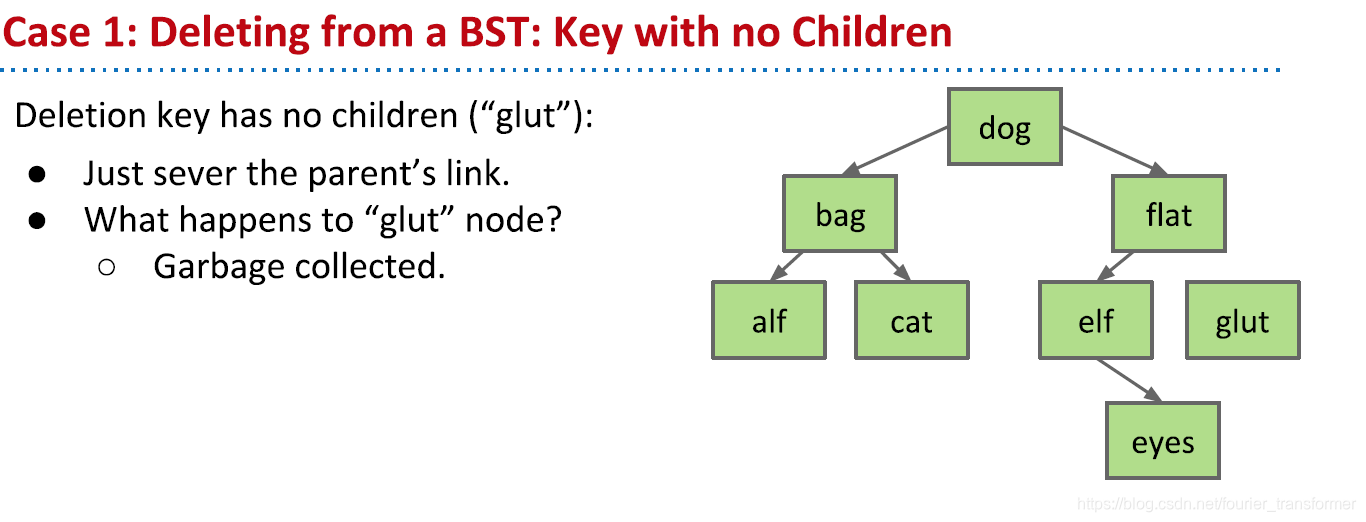
没有children的，直接删除。

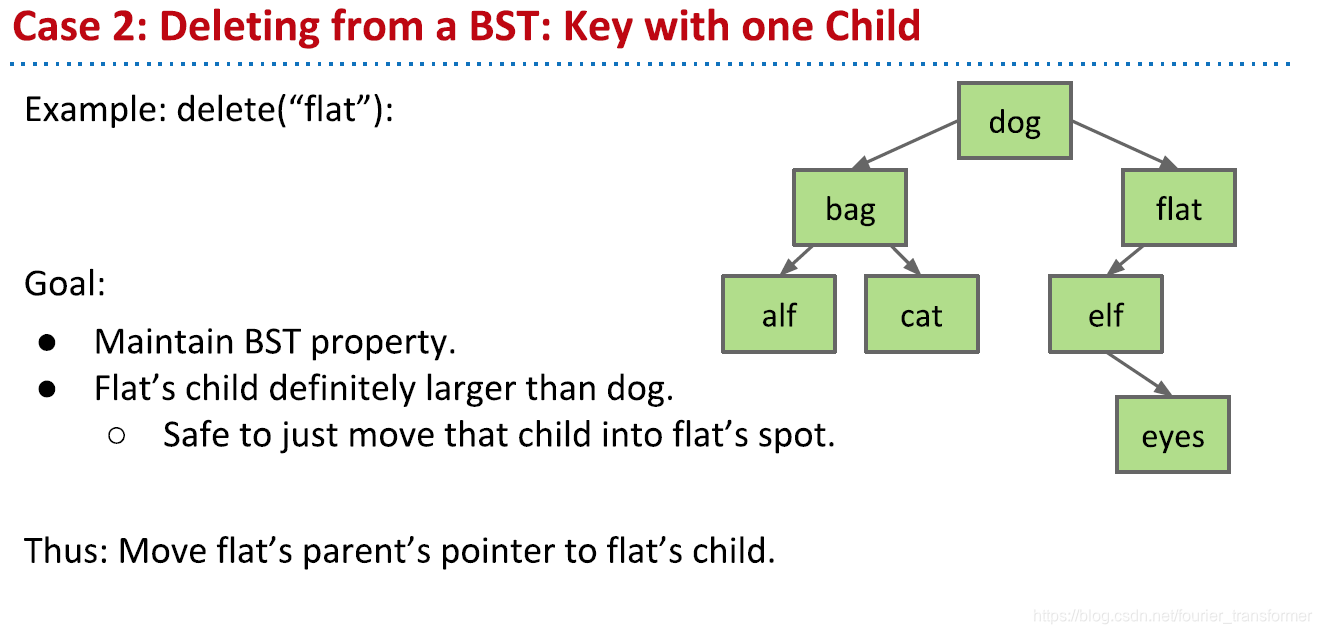
有一个child的，将父节点指向自己的指针指向child。

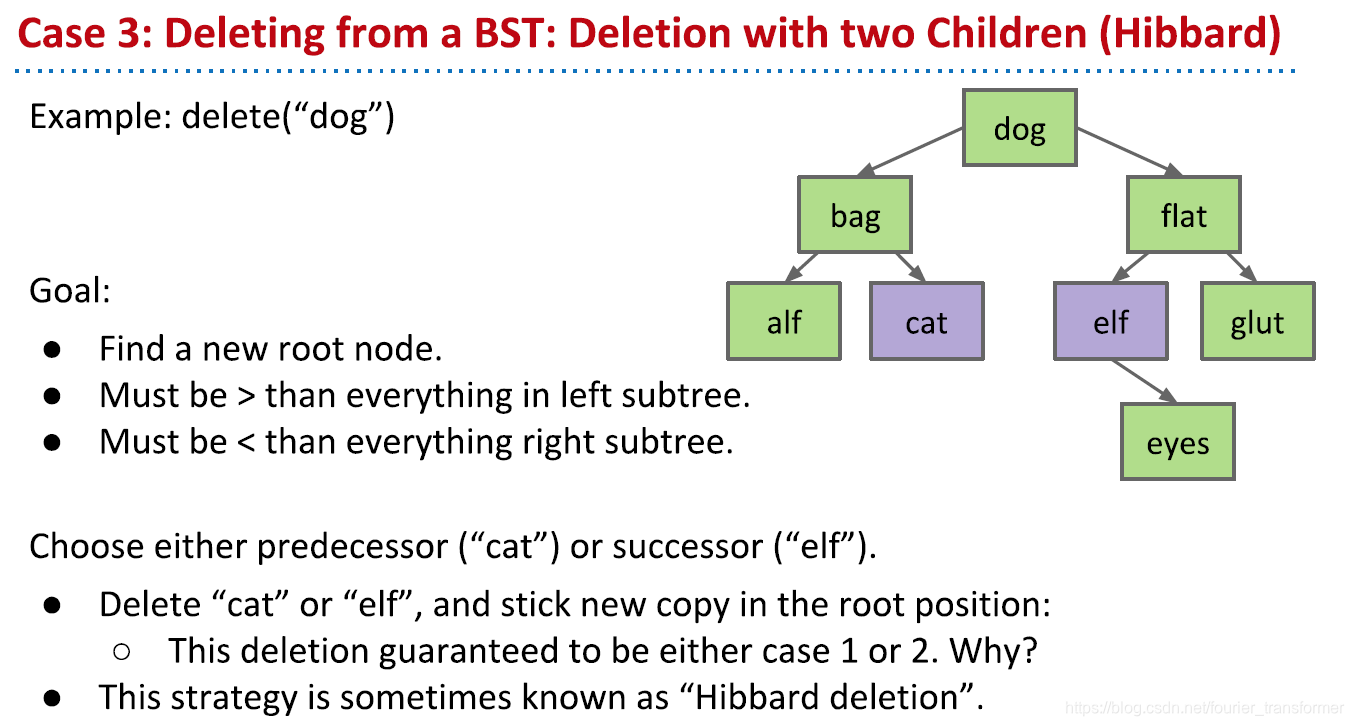
有两个children的，需要拷贝左子树最右边的节点或者右子树最左边的节点，删除，然后放在删除节点相同的位置上。原因在于删除的节点是一个中间节点，删除之前需要找到一个新的中间节点替代，要不树就散了，中间节点需要大于左子树所有值，小于右子树所有值，所以自然想到取以上两个节点。