LeetCode:105. 从前序与中序遍历序列构造二叉树

核心点：
1.前序遍历：根左右 ；中序遍历：左根右

2.从前序遍历中的子树preorder，第一个元素即为根节点，创建出根节点head,最后用来返回

3.接着就从中序遍历中的子树inorder，遍历找到根节点对应的索引find,[L2,find)即为左子树元素，(find,R2]即为右子树元素，find - L2的根节点到左子树边界距离长度就等同于中序遍历中根节点到左子树边界距离，从而来确定左子树的右边界： L1 + find - L2 ，其余边界同理推断

4.然后开始用根节点head递归去构造head.left head.right左右子树

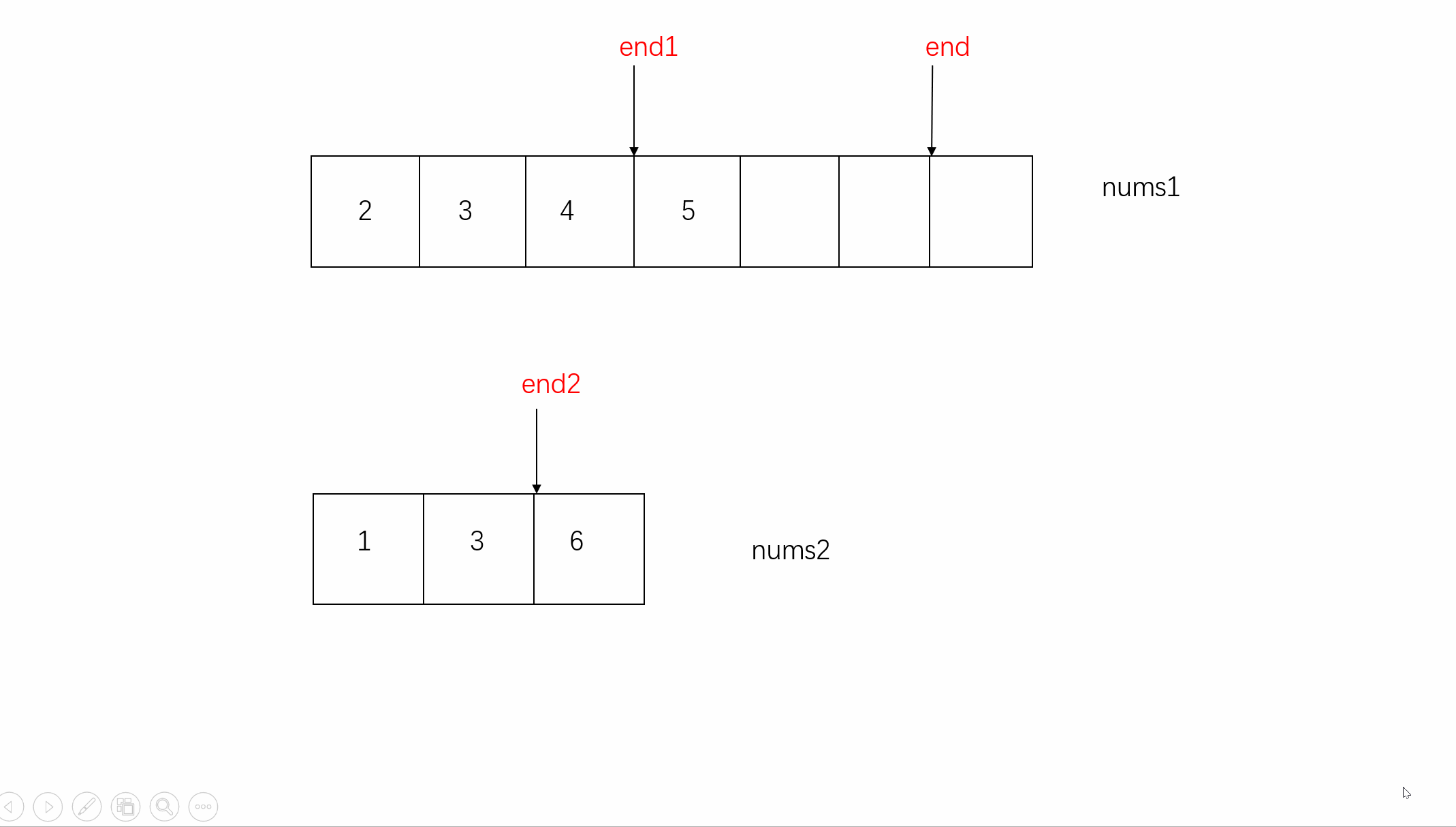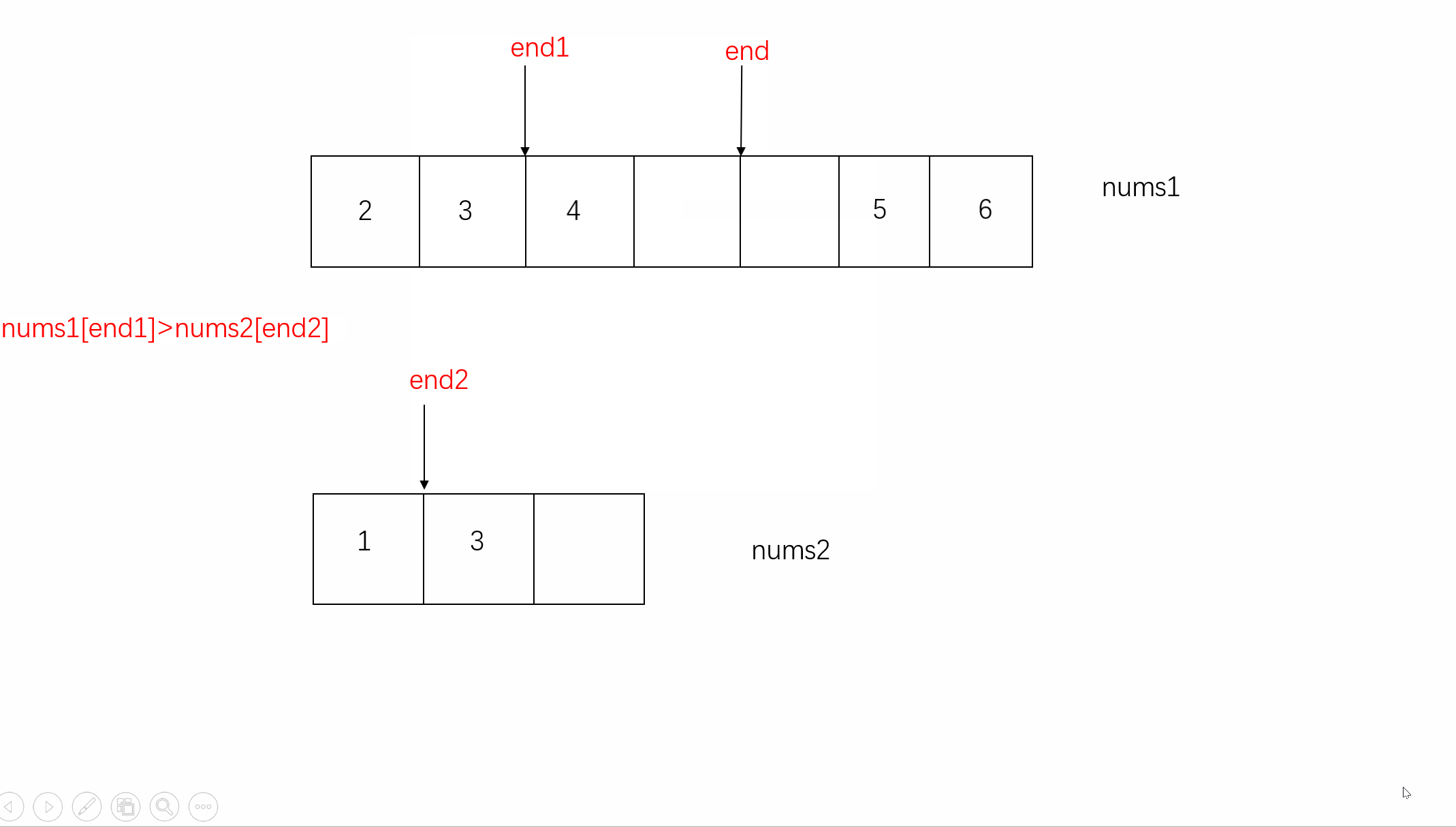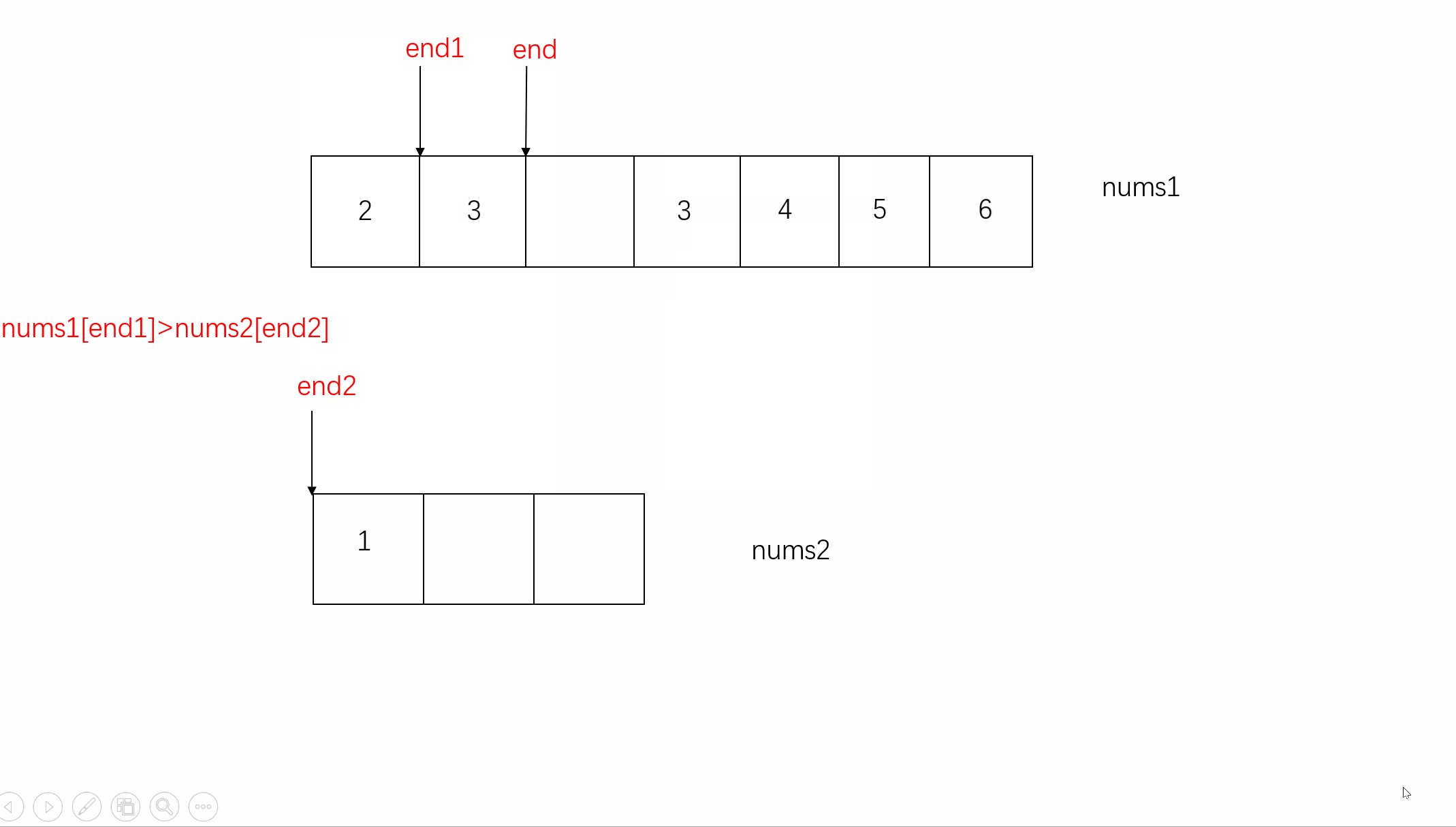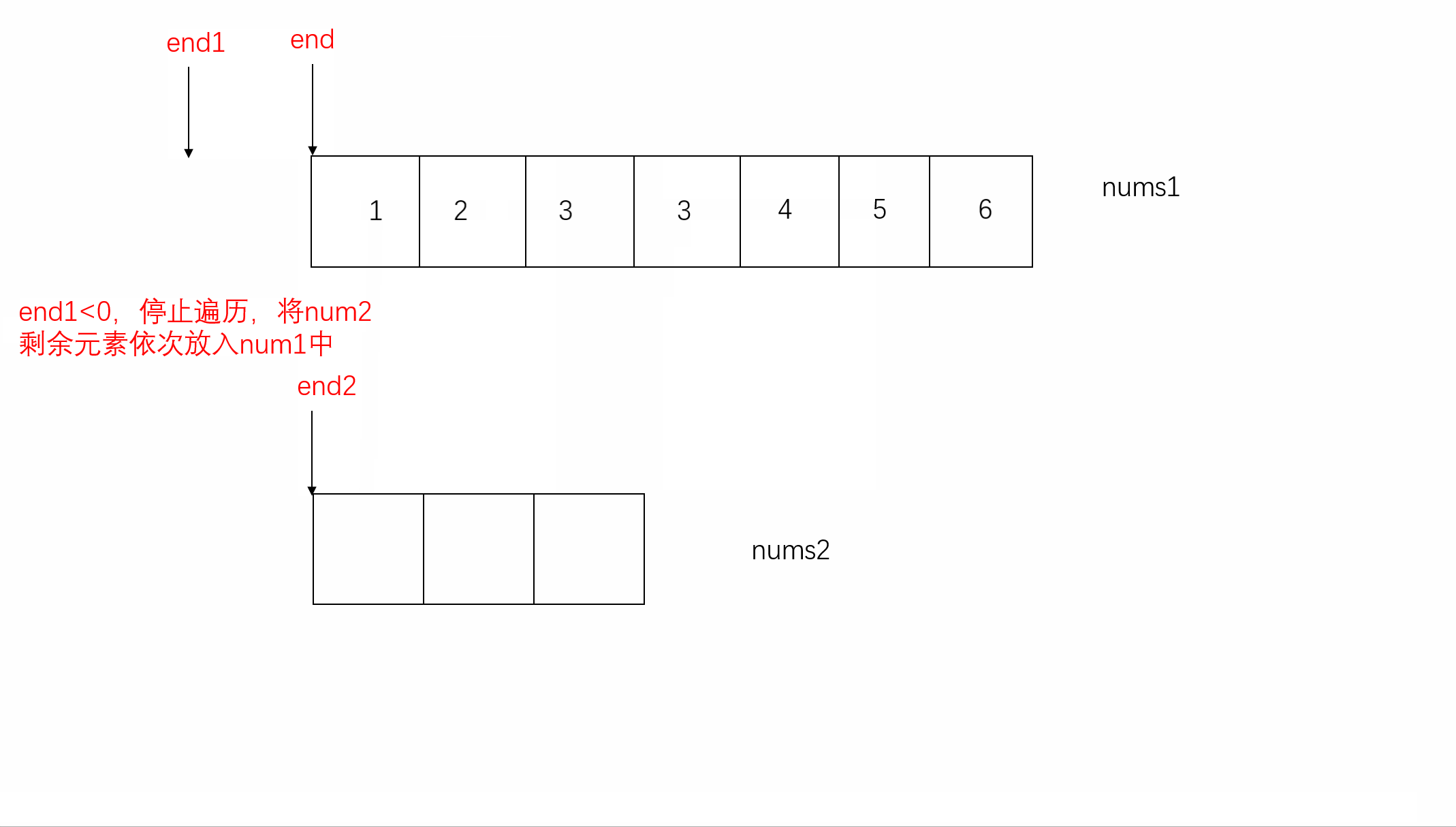
5.L1 > R1边界溢出，这点很重要容易忽略，会出现二叉树是一个单边树，即左子树空或者右子树空，此时就会存在越界情况：比如先序 中序 都为[1,2,3] (左子树为空) ，根节点1，中序遍历中索引find=0，再往左找左子树递归就溢出了。head.left = f(preorder, L1 + 1, L1 + find - L2, inorder, L2, find - 1,valueIndexMap); 此时L1 + find - L2 = L1 因为第一轮find跟L2重叠 所以就变成L1+1,L1 溢出，则需要返回空

/*** Definition for a binary tree node.* public class TreeNode {*     int val;*     TreeNode left;*     TreeNode right;*     TreeNode() {}*     TreeNode(int val) { this.val = val; }*     TreeNode(int val, TreeNode left, TreeNode right) {*         this.val = val;*         this.left = left;*         this.right = right;*     }* }*/
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {//提前记录中序遍历的头节点对应索引的Map,用来查询出中序遍历中哪个是根节点，对应的索引，就不用每次递归子树时都要循环查找中序遍历的根节点HashMap<Integer,Integer> valueIndexMap = new HashMap<>();for(int i = 0; i < inorder.length; i++){valueIndexMap.put(inorder[i], i);}return f(preorder, 0, preorder.length-1, inorder, 0, inorder.length-1, valueIndexMap);}// 有一棵树，先序结果是pre[L1...R1]，中序结果是in[L2...R2]// 请建出整棵树返回头节点public TreeNode f(int[] preorder, int L1, int R1, int[] inorder, int L2, int R2, HashMap<Integer,Integer> valueIndexMap){//存在某些情况下 会越界溢出//比如 先序 中序 都为[1,2,3] (左子树为空) 那么确定好根节点1，中序遍历中该根节点在索引find=0，在往左找左子树递归就溢出了。head.left =  f(preorder, L1 + 1, L1 + find - L2, inorder, L2, find - 1,valueIndexMap); 此时L1 + find - L2 = L1  因为第一轮find跟L2重叠 所以就变成L1+1,L1 溢出，返回空if(L1 > R1) return null;//先序遍历 根左右，索引第一个即为根节点 取出TreeNode head = new TreeNode(preorder[L1]);//当子树中只有自己的时候则直接返回根节点if(L1 == R1)return head;//从中序遍历中，找到根节点L1对应的索引find ,那么 从[0,find-1]皆为左子树的节点，//[find+1,R2]皆为右子树的节点，然后就开始分别左递归，右递归去构建树int find = valueIndexMap.get(preorder[L1]);//递归左子树：确定先序遍历的左子树左右边界：左边界就是从L1+1,因为L1是根节点，根据中序遍历根节点索引find往左的元素都为左子树元素，find - L2 表示根节点到左子树左边界的距离，那么在先序遍历中根节点加上这个距离就得到左子树的右边界了。 因为两边同个子树长度一定相等。 所以右边界为 L1+find-L2;    而中序遍历的左子树左右边界：就是find节点左侧那一堆数 L2,find-1//head.left = f(preorder, L1 + 1, L1 + find - L2, inorder, L2, find - 1,valueIndexMap);//递归右子树同理head.right = f(preorder,L1 + find - L2 + 1, R1, inorder, find + 1, R2,valueIndexMap);//最后需要返回根节点return head;}
}