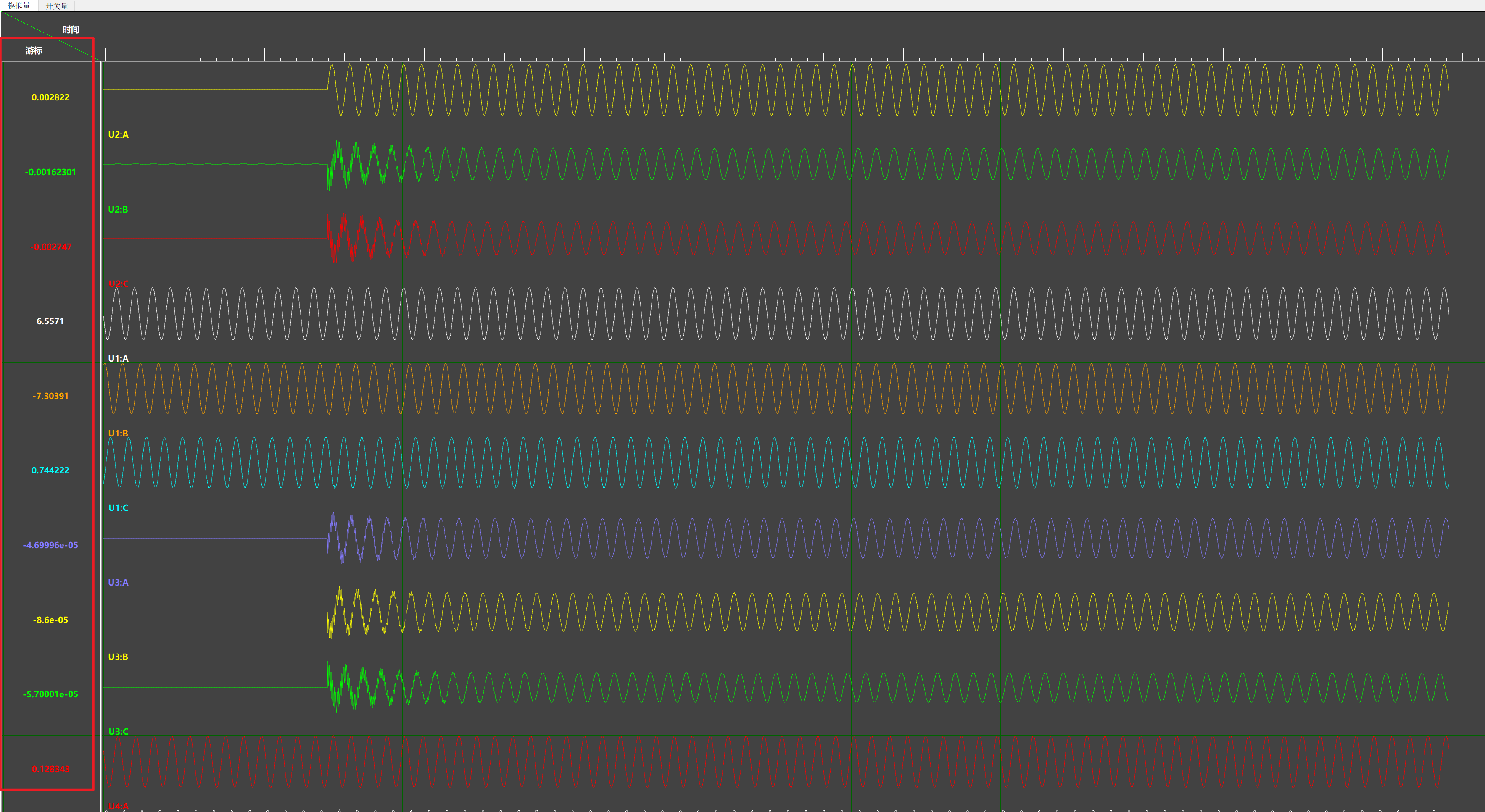
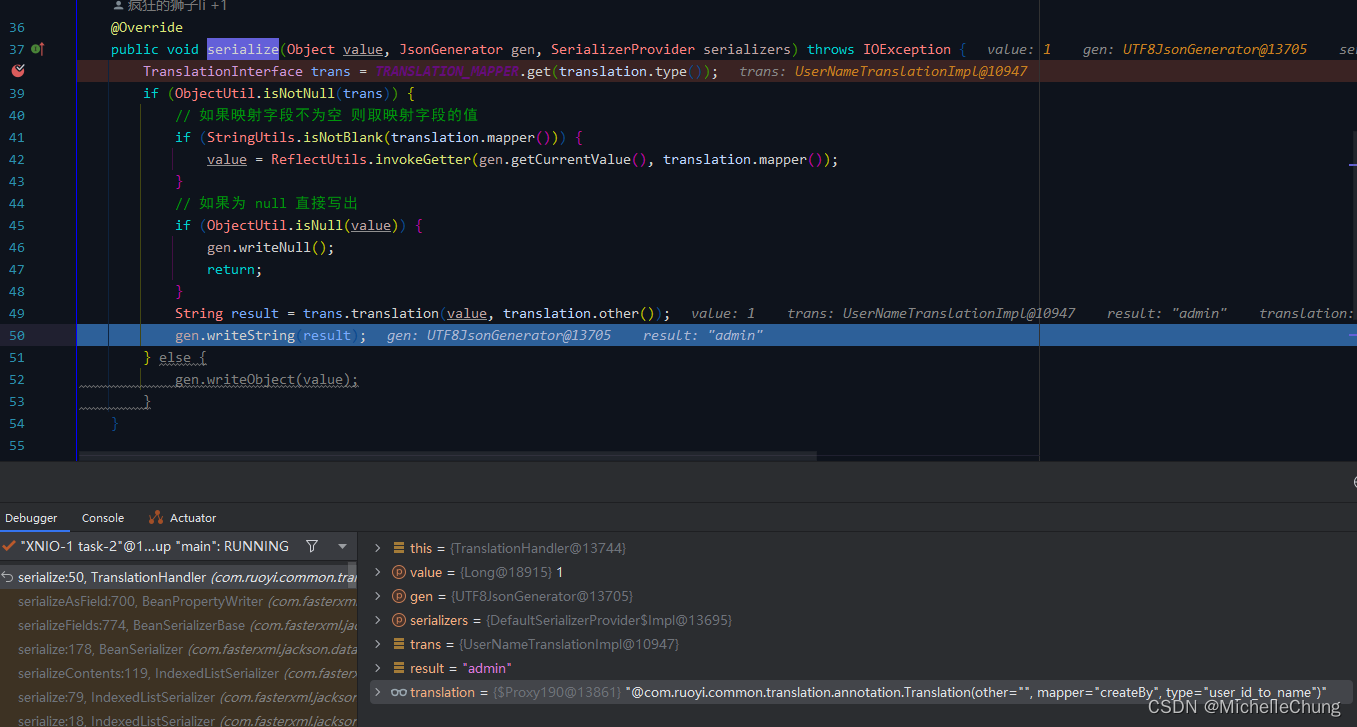
贪心算法特点
从局部最优解推出全局最优,并且想不出来反例。贪心没有明确有规律的套路,而对于贪心的难题,更多的是难在思路上,要用一些转化问题的思维方法,然后,再根据局部最优解推出全局最优。
参考文章:贪心算法理论基础
1、发饼干
先排序,按饼干从小到大的顺序,依次分给从小到大排序的小朋友。
127、【贪心算法】leetcode ——455. 分发饼干:DFS+双指针法(C++版本)
2、0 水准线
-
count用来记录当前子序列的相加和,当count大于0时,继续相加。当count小于或等于0时,重新开始选取子序列。
以count是否为0判定的原因:若后续为正数时,没有这个负数更好,若后续为负数时,越加只会越小)
129、【贪心算法】leetcode ——53. 最大子数组和(贪心算法)(C++版本) -
满足条件的差值总和一定大于等于0,起始点之后区间一定大于等于0,区间小于时,更新起始点。
134、【贪心算法】leetcode ——134. 加油站(贪心策略)(C++版本)
3、高度差模型问题
将问题图形化为高度差模型,根据题中会有的情况,出现某一坡度情形时,执行对应的情况。
-
获取每个“小山峰”(前升坡,后降坡)
128、【贪心算法】leetcode ——376. 摆动序列(C++版本):判定之前高度差和当前高度差的正负情况 -
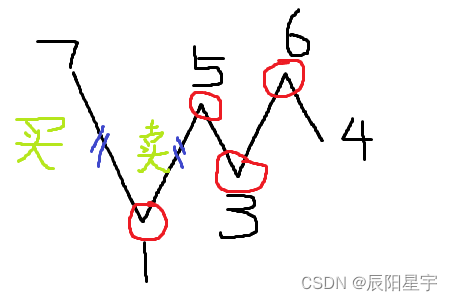
获取每个“上升坡度”
130、【贪心算法】leetcode ——122. 买卖股票的最佳时机 II(贪心算法)(C++版本):升坡时进行一次买卖,降坡或平坡时只买不卖。
4、区间问题
(1)区间范围问题
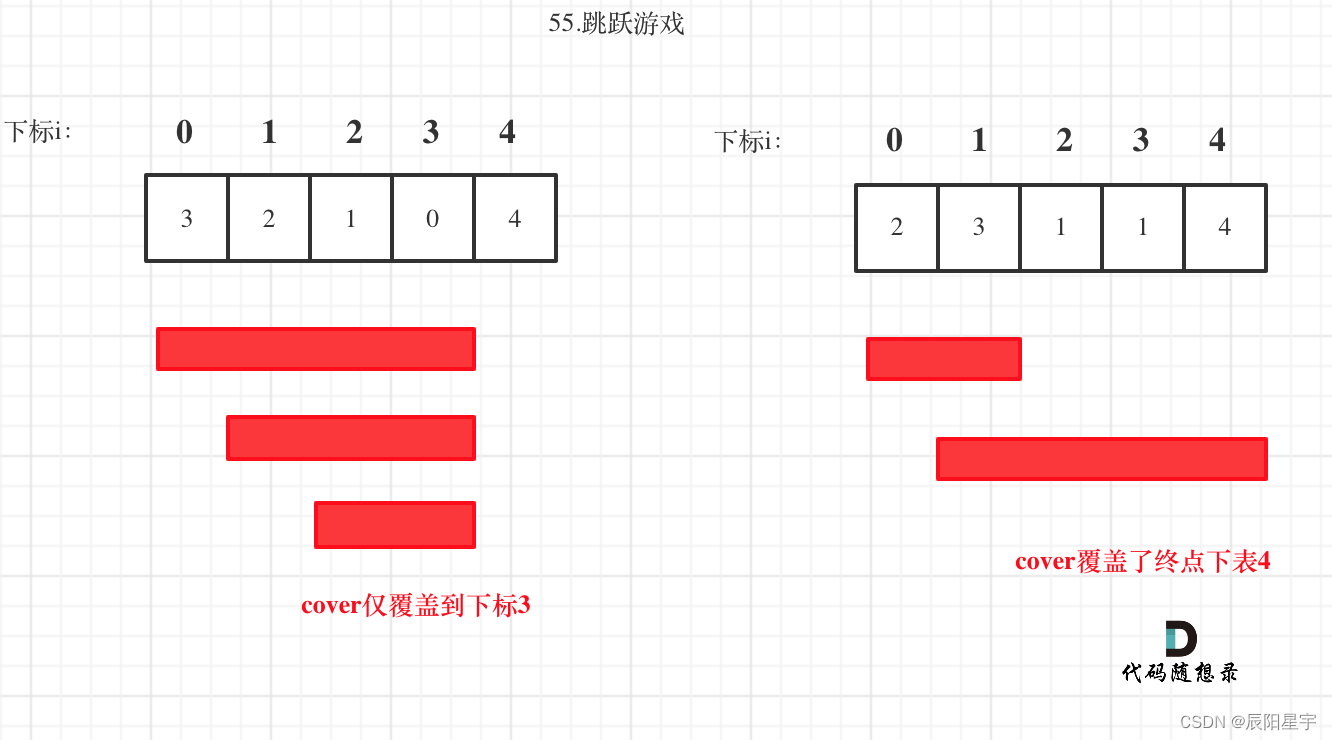
将问题转化为区间覆盖问题,更新区间右边界,看最大区间能否覆盖到最后一个位置
-
每次获取最大跳跃步数
131、【贪心算法】leetcode ——55. 跳跃游戏(贪心策略)(贪心算法)(C++版本):每次在区间范围内移动,获取最大可覆盖范围 -
在当前可获取的最大跳跃范围内,找到最优位置
132、【贪心算法】leetcode ——45. 跳跃游戏 II(贪心策略)(C++版本) :在给定的跳跃范围内寻找最优跳跃位置(后续跳跃距离更远),到达最大范围边界时,进行跳跃更新。 -
更新最远区间边界
140、【贪心算法】leetcode ——763. 划分字母区间(区间边界更新)(C++版本):先记录每个字母的最远位置,每获取一个字母就查看是否会有更远区间,更新区间边界,到达边界时,更新起始边界继续遍历。
(2)区间重叠问题
先按从打到小或从小到大排序,每次对前后两个区间关系进行判断,对重叠区间或非重叠进行操作。
两区间关系:
(1)不重叠
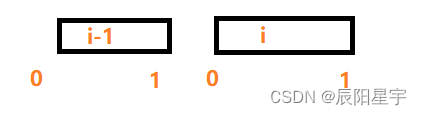
(2)交叉重叠
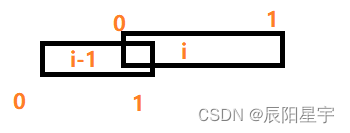
(3)包含重叠
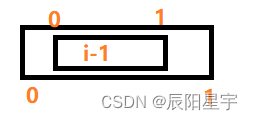
-
更新区间
138、【贪心算法】leetcode ——452. 用最少数量的箭引爆气球(贪心重叠问题)(C++版本):重叠时候更新最后一个气球的右区间,不重叠时弓箭数加一。 -
法一: 以左边界排序,更新右边界,法二: 以有边界排序,记录不重叠区间
139、【贪心算法】leetcode ——435. 无重叠区间(更新区间+记录不重叠区间)(C++版本) -
合并重叠区间
141、【贪心算法】leetcode ——56. 合并区间(区间重叠解法+双指针解法)(C++版本):前后量区间对比,有重叠合并,无重叠,将前面的加入结果集。
5、多维度问题
需要考虑多个条件,若仅一趟遍历会很复杂,因此将每一个维度分成一趟遍历情况。
-
左值大于右值,左值小于右值,两个维度
135、【贪心算法】leetcode ——135. 分发糖果(多维度贪心)(C++版本):第一趟,从左到右遍历,对于左值<右值,进行加一。第二趟,再从右到左遍历,对于右值>左值,取max(上述已完成数值, 右值+1)。 -
身高从大到小,大于此身高的个数,两个维度
137、【贪心算法】leetcode ——406. 根据身高重建队列(多维度贪心)(C++版本):第一趟,按从大到小排列。第二趟,在第一趟的基础上,将人数作为插入下标,插入结果集。
6、模拟变化
-
K次取反
133、【贪心算法】leetcode ——1005. K 次取反后最大化的数组和(模拟变化+贪心策略)(C++版本):先变负数,若K对负数操作完后还不为0,对最小非负数进行操作,奇数时取反,偶数时不变。 -
根据各种情况进行操作
135、【贪心算法】leetcode ——860. 柠檬水找零(贪心策略)(C++版本):先找大钱,再找小钱
7、单调递增的数字
根据最大递增数的特性,当不满足情况时,改变第i位为9,第i - 1位的数值位数减一。
143、【回溯算法】leetcode ——738. 单调递增的数字:暴力法+贪心法(C++版本)