1002
- 题意


- 思路
深搜,每个格子都搜一遍。技巧dfs(cnt,ans)dfs(第几个格子,答案);
- 代码
#include <iostream>using namespace std;int n,i,j,ans;
char s[5][5];int c_put(int n,int m)
{for (i = n-1;i >= 0;i --) {if (s[i][m] == 'O')return 0;if (s[i][m] == 'X') break;}for (j = m-1;j >= 0;j --) {if (s[n][j] == 'O')return 0;if (s[n][j] == 'X')break;}return 1;
}void dfs(int k,int num)
{int x,y;if (k == n*n) {if (num > ans) {ans = num;}return ;}else {x = k/n;y = k%n;if (s[x][y] == '.'&&c_put(x,y)) {s[x][y] = 'O';dfs(k+1,num+1);s[x][y] = '.';}dfs(k+1,num);}
}
int main()
{while (cin>>n&&n) {ans = 0;for (i = 0;i < n; i++) {for (j = 0;j < n;j ++) cin>>s[i][j];}dfs(0,0);cout<<ans<<endl;}return 0;
}
1003
- 题意
在每年的6月1日儿童节,电视上都会有一个名为 "撞气球 "的游戏。 规则非常简单。 地上有100个贴有标签的气球,数字为1到100。 在裁判员喊出 "开始吧!"之后,两位选手开始时的分数都是 “1”,他们竞相用脚去撞气球,同时,他们的分数要乘以他们所撞气球上写的数字。 一分钟后,小观众们被允许把剩下的气球拿走,每个参赛者报告他/她的分数,即他/她撞破的气球上的数字的乘积。 非官方的赢家是宣布最高分数的选手。
但不可避免的是,会出现争议,因此在争议解决之前,不会确定正式的赢家。 声称分数较低的选手有权质疑其对手的分数。 得分较低的选手被认为是说了实话,因为如果他(她)要对自己的分数撒谎,他(她)肯定会想出一个更大更好的谎言。 如果分数较高的玩家的分数不能被挑战者撞碎的气球所达到,则挑战成功。 因此,如果挑战成功,声称分数较低的玩家获胜。
因此,例如,如果一个玩家声称得到343分,另一个声称得到49分,那么显然第一个玩家在撒谎;得到343分的唯一方法是撞毁标有7和49的气球,而得到49分的唯一方法是撞毁标有49的气球。 由于这两个分数都需要撞毁标有49的气球,那么声称得到343分的人就被认为是在撒谎。
另一方面,如果一个人声称得了162分,另一个人声称得了81分,那么两个人都有可能说的是实话(例如,一个人撞坏了2、3和27号气球,而另一个人撞坏了81号气球),所以挑战不会被支持。
顺便说一下,如果挑战者在计算他/她的分数时犯了一个错误,那么挑战将不会被支持。例如,如果一个玩家声称10001分,另一个声称10003分,那么显然他们都没有说实话。在这种情况下,挑战将不会被支持。
不幸的是,任何愿意担任撞气球游戏裁判的人都有可能在炎热的气氛中过度兴奋,不能合理地期望她进行裁判所需的复杂计算。 因此,需要你,清醒的程序员,提供一个软件解决方案。
- 思路
搜索,看看a,b假设a>b;是否都能够得到,如果a不能,那么就是b胜。
否则就是a胜
关键代码:
if (b == 1) {bTrue = 1;if (a == 1) aTrue = 1;}
这样aTrue 判断是在b(小数)已经可以的情况下。
- 代码
#include <cstdio>
#include <iostream>
#include <cstring>using namespace std;bool aTrue,bTrue;void judge(int a,int b,int p)
{if (b == 1) {bTrue = 1;if (a == 1) aTrue = 1;}if (p == 1||(aTrue == 1&&bTrue == 1))return ;if (a%p == 0)judge(a/p,b,p-1);if (b%p == 0) judge(a,b/p,p-1);judge(a,b,p-1);
}int main()
{int a,b;while (scanf("%d%d",&a,&b) != EOF) {if (a < b)swap(a,b);aTrue = false;bTrue = false;judge(a,b,100);if (!aTrue && bTrue) {printf("%d\n",b);} else {printf("%d\n",a);}}
}
1031
- 题意
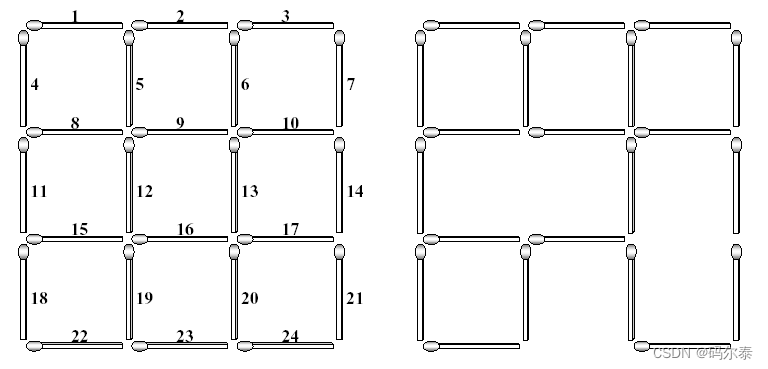
下面的左图是用2(34)(=24)根火柴棒做成的一个完整的33格。所有火柴棒的长度都是一。你可以在网格中找到许多不同大小的正方形。一个正方形的大小就是它的边的长度。在左图所示的网格中,有9个大小为1的正方形,4个大小为2的正方形,1个大小为3的正方形。
如左图所示,完整的网格中的每根火柴棒都有一个独特的编号,从左到右、从上到下分配。如果你从完整的网格中抽出一些火柴棒,那么网格中的一些方格就会被破坏,这就导致了一个不完整的33号网格。右图显示的是除去三根编号为12、17和23的火柴棒后的不完整的33网格。这一移除行为破坏了5个大小为1的方格,3个大小为2的方格,以及1个大小为3的方格。因此,这个不完整的网格没有大小为3的方格,但仍有4个大小为1的方格和1个大小为2的方格。
作为输入,你将得到一个由不超过2n(n+1)根火柴棍组成的(完整或不完整的)nn网格,而自然数n<=5。你的任务是计算取出的火柴棒的最小数量,以破坏输入的nn个网格中的所有方格。
- 思路
此问题可以转化为一个图论的问题,把火柴看作另A类结点,正方形看作B类结点。
如果某根火柴在某个正方形的边上,那么我们就往这相应的两个结点添加一条边。
这样,问题转化为求该图中,最少用多少A类结点可以覆盖所有的B类结点。
当n=5时,A类结点数为:2n(n+1)=60;B类结点数为:n(n+1)(2n+1)/6=55。
可以见得,B类结点可以直接通过一个64位整型类储存。利用位运算,可以大大加快搜索速度。做法具体如下:
(1) 若有边(i, j)(分别属于A、B类结点,下同),则Aij = 0;否则Aij = 1;
(2) 对于每个确定的i,将Aij二进制编码至Bi中;
(3) 除去数据中没有的Bi,并编码初始状态st;
(4) 对于Bi按照可覆盖点数排序(优化1);
(5) 若i<j,且Bi和Bj效果是一致的,则删掉Bj(优化2);
(6) 计算opt[i] = Bi & B(i+1) & B(i+2) … & Bn(可行性剪枝)。
搜索过程,按照一般的方法做即可,添加最优性剪枝:若当前值大于阶段最剪枝,则跳出;
添加可行性剪枝,若取剩余所有的Bi也无法达到目标,则剪枝。 - 代码
#include <iostream>
#include <vector>
#include <cstring>
using namespace std;long long rest,cover[60],remain[60];int Size,cnt,ans;
int up[6][6];
bool stick[60];void initUP()
{int i,j;for (i = 0;i < Size;i ++) {up[i][0] = i*(Size*2+1);for(j = 1;j < Size;j ++) {up[i][j] = up[i][j-1] + 1;}}
}void initCover(int firststick,int sqsize,long long mask)
{int i;int gap = 2*Size+1;int num = firststick;for (i = 0;i < sqsize;i ++) {cover[num] |= mask;cover[num+sqsize*gap] |= mask;num ++;}num = firststick + Size;for (i = 0;i < sqsize;i ++) {cover[num] |= mask;cover[num+sqsize] |= mask;num = num + gap;}
}void input()
{int i,j,k,n;cin>>Size;initUP();cin>>cnt;memset(stick,true,sizeof(stick));for (i = 0;i < cnt;i ++) {cin>>n;stick[n-1] = false;}long long mask = 1;memset(cover,0,sizeof(cover));for (i = 1;i <= Size;i ++) {for (j = 0;j <= Size-i;j ++) {for (k = 0;k <= Size-i;k ++) {initCover(up[j][k],i,mask);mask<<=1;}}}
}void modify()
{int i,j,rec;rec = Size*(Size+1)*(2*Size+1)/6;rest = 1;for (i = 1;i < rec;i ++) {rest <<= 1;rest += 1;}cnt = 2*Size*(Size+1);for (i = 0;i < cnt ;i ++) {if (!stick[i]) rest &= ~cover[i];}for (i = 0;i < cnt;i ++) {cover[i] &= rest;}for (i = 0;i < cnt;i ++) {if (!stick[i]) continue;else {for (j = 0;j < cnt;j ++) {if (j != i&&((cover[i]&cover[j]) == cover[j]))stick[j] = false;}}}int c = 0;for (i = 0;i < cnt;i ++) {if (stick[i]) {cover[c ++] = cover[i];}}cnt = c;remain[cnt -1 ] = cover[cnt - 1];for (i = cnt-2;i >= 0;i --) {remain[i] = remain[i+1]|cover[i];}
}void dfs(int c,int last,long long state)
{if (state == rest) {ans = c;return;} else {if (c < ans&&(remain[last+1]|state) == rest) {for (int i = last+1;i < cnt;i ++) {if ((cover[i]|state)>state) {dfs(c+1,i,state|cover[i]);}}}}
}int main()
{int num;cin>>num;while (num --) {input();modify();ans = 30;dfs(0,-1,0);cout<<ans<<endl;}return 0;
}