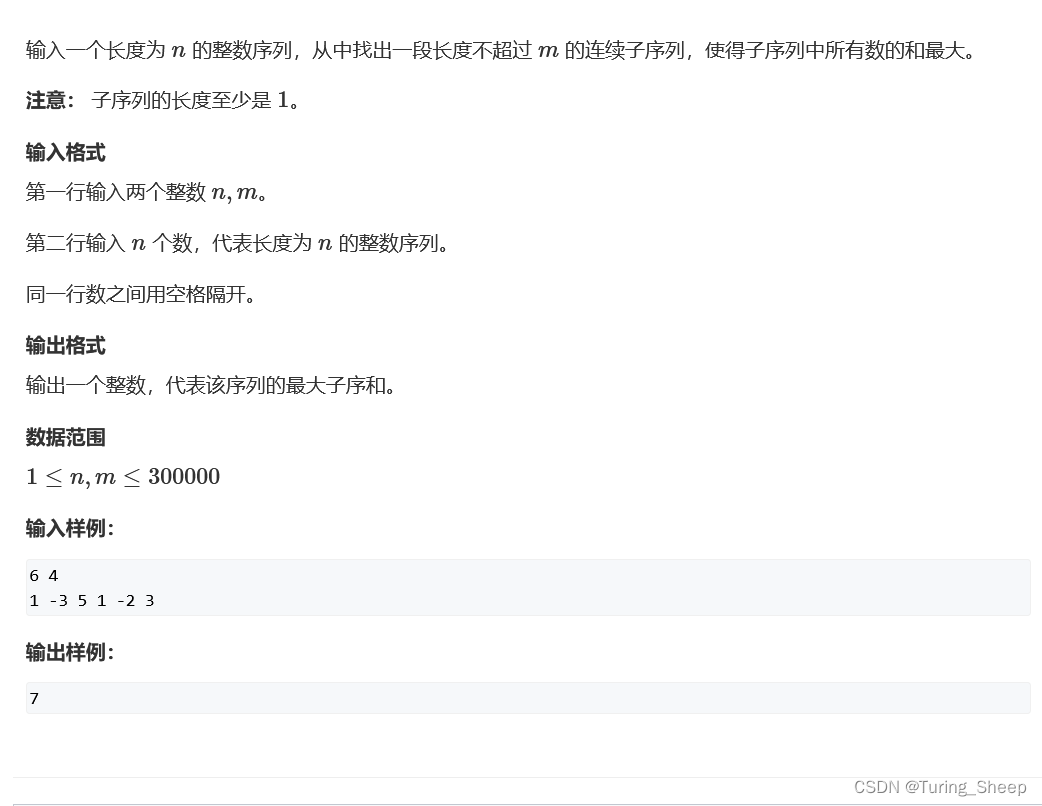
一、问题

二、分析

涉及到一段区间和的问题，我们最容易想到的是前缀和算法。

因此，我们可以假设我们的最优解区间是$[l,r]$，同时将前缀和数组记作$s[i]$，那么我们的区间和就可以表示为$s[r]-s[l-1]$，假设我们固定一右端点$r$，那么如果想要让这个差值最大，在$s[r]$不变的情况下，只能是$s[l-1]$最小。

也就是说，我们需要在$r$的右侧寻找一个最小值，但是这个最小值的所在范围是有一定约束的，因为题目中说的是区间长度不超过$m$，所以我们需要在$r$右侧$m+1$的范围内找一个最小值。

为什么是$m+1$?

因为我们想要找$[l,r]$的区间和，用到的是$s[l-1]$，也就是说如果区间长度是$m$，我们减去的是左侧距离$m+1$的那个数。

而随着右端点的移动，这个长度为$m$的范围也在向右移动，相当于一个滑动窗口。

而对于滑动窗口求最值的方法就是我们在之前介绍过的单调队列。

如果读者对单调队列不熟悉的话，作者在算法专栏中写过一篇文章：第九章：单调栈与单调队列，这里面详细地介绍了该算法和一些关键点的讨论。

这里就直接用单调队列了。

因此，我们只需要枚举右端点，一边枚举右端点一边更新滑动窗口。

这道题其实和DP没有太大的关系。

只不过我们的右端点$r$是从小到大枚举的，类似于DP从小到大求解问题的思想。

但状态和状态之间没有必然的联系。

三、代码

#include<bits/stdc++.h>
using namespace std;
const int N = 3e5 + 10;
int a[N], s[N];
int q[N], h, t;
void solve()
{int n, m;cin >> n >> m;for(int i = 1; i <= n; i ++ ){scanf("%d", a + i);a[i] += a[i - 1];}int res = -0x3f3f3f3f;for(int i = 1; i <= n; i ++ ){if(h <= t && q[h] < i - m )h++;res = max(res, a[i] - a[q[h]]);while(h <= t && a[q[t]] >= a[i])t--;q[ ++ t] = i;}cout << res << endl;
}int main()
{solve();return 0;
}