一共有两种方法Prim算法和Kruskal算法都可以看作是应用贪心算法设计策略的例子。

Prim算法--选集合S中所有顶点的邻接点距离最短的那个点（不属于S）加入集合S

Kruskal算法--每次选取最短的且不构成回路的边

它们都利用了下面的最小生成树性质：如果途中具有最小权值的边只有一条，那么这条边包含在任意一个最小生成树中。

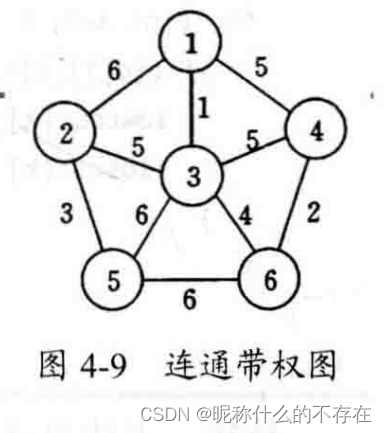
设G=(V,E)是连通带权图，U是V的真子集。如果(u,v)属于E，且顶点u属于U，顶点v属于V-U，且在所有这样的边中，(u,v)的权c[u][v]最小，那么一定存在G的一棵最小生成树，它以(u,v)为其中一条边。这个性质有时也称为MST性质。

Prim算法--选集合S中所有顶点的邻接点距离最短的那个点（不属于S）加入集合S

Prim算法的每一步都会为一棵生长中的树添加一条边，该树最开始只有一个顶点，然后会添加V−1个边。每次总是添加生长中的树和树中除该生长的树以外的部分形成的切分的具有最小权值的横切边。

描述：首先S中只有一个顶点S={1},然后，只要S！=V说明点还没有取完，就贪心选择满足条件的距离S中最小得边(i,j)，把不在S集合中的顶点j添加到S集合中，一直循环到S=V结束

条件是什么？--选集合S中所有顶点的邻接点距离最短的那个

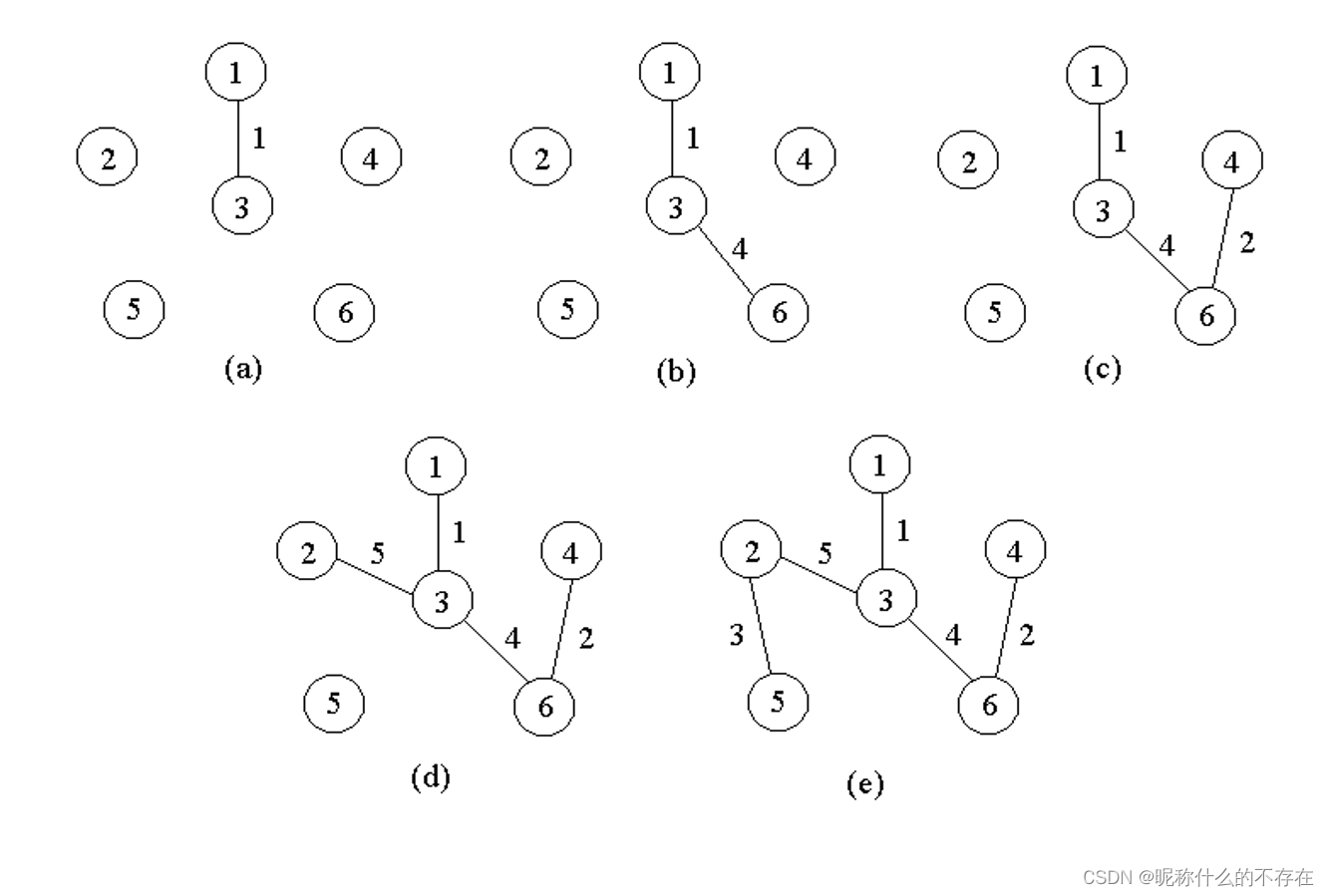
按Prim算法选取边的过程如下页图所示

Kruskal算法--每次选取最短的且不构成回路的边

首先将G的n个顶点看成n个孤立的连通分支。将所有的边按权从小到大排序。

然后从第一条边开始，依边权递增的顺序查看每一条边，并按下述方法连接2个不同的连通分支：当查看到第k条边(v,w)时，如果端点v和w分别是当前2个不同的连通分支T1和T2中的顶点时，就用边(v,w)将T1和T2连接成一个连通分支，然后继续查看第k+1条边；如果端点v和w在当前的同一个连通分支中，就直接再查看第k+1条边。

这个过程一直进行到只剩下一个连通分支时为止。

伪代码

代码Prim

//最小生成树Prim算法 
/*每次将能到达的最短的边加进去 
closest[j]是j在S中的邻接顶点,
先找出V-S中使c[j][closest[j]](即lowcost[j]) 值最小的顶点j,
然后根据数组closest选取边(j,closest[j]),然后将j添加到S中,
最后对closest和lowcost做修改 
*/
#include<iostream>
#include<fstream>
#include<string.h>
#define INF 0x3f3f3f
using namespace std;ifstream fin("4d6.txt");
int n,m;//n个顶点，m条边
int c[100][100];
int s[1000];//s[i]=1表示顶点i被挑出来了，在生成树里了 
int closest[1000];//closest[j]是j在S中的邻接顶点
int lowcost[1000];//lowcost[j]就是c[j][closest[j]] 
void Prim(){for(int i=2;i<=n;i++){//初始化 lowcost[i]=c[1][i];closest[i]=1;s[i]=0; }s[1]=1; for(int i=1;i<n;i++){int t=INF;int j=1;//从第一个结点开始 for(int k=2;k<=n;k++){if(lowcost[k]<t && !s[k]){t = lowcost[k]; j=k;}}cout<<"("<<closest[j]<<","<<j<<")= "<<lowcost[j]<<endl;s[j]=1;for(int k=2;k<=n;k++){if(c[j][k]<lowcost[k] && !s[k]){lowcost[k] = c[j][k];closest[k]=j;		}}}
}
int main(){//cin>>n>>m;fin>>n >> m;int i,j;int x,y,z;for(i=0;i<=n;i++) //初始化 for(j=0;j<=n;j++)c[i][j]=INF;for(i=0;i<m;i++){fin>>x>>y>>z;c[x][y]=z;c[y][x]=z;} cout<<"Prim:依次加入的顺序为：\n";	Prim();return 0;
}

代码kruskal

//最小生成树Kruskal
//每次选图中权值最小的边 
#include<iostream>
#include<string.h>
#include<fstream>
#include<algorithm>
using namespace std;
ifstream fin("4d6.txt");
int n,m;//n个顶点，m条边
int s[1000];//并查集s[i]=1表示顶点i的父结点是1，即i与1在一个集合
struct edge{int u,v,w;//顶点u到顶点v的权重是w(无向图) 
}g[1000];
bool comp(edge a,edge b){return a.w < b.w;
}
void Init(){for(int i=0;i<m;i++){s[i]=i;//初始化，现在各自为王，自己就是一个集合}
} 
int Find(int x){//查询根结点if(s[x]==x)return x;else{s[x]=Find(s[x]);  //顺便把双亲结点也设置为根结点，路径压缩return s[x];}	
}
void Merge(int x,int y){//合并,把 y 合并到 x 中去，就是把y的双亲结点设为xs[Find(y)] = Find(x);
}
void Kruskal(){int x,y;for(int i=0;i<m;i++){x = g[i].u;y = g[i].v;if(Find(x) != Find(y)){cout<<"("<<x<<","<<y<<")= "<<g[i].w<<endl;Merge(x,y);}}
}
int main(){fin>>n>>m;int i;int x,y,z;for(i=0;i<m;i++){fin>>x>>y>>z;g[i].u=x;g[i].v=y;g[i].w=z;} sort(g,g+m,comp);Init();cout<<"依次加入的顺序为:\n";Kruskal();return 0;
}

测试样例

6 10
1 2 6
1 3 1
1 4 5
2 3 5
2 5 3
3 4 5
3 5 6
3 6 4
4 6 2
5 6 6