一.最小生成树

1.1概念

1.2Kruskal算法

1.3Prim算法

二.最短路径

2.11单源最短路径--Dijkstra算法

2.1.2单源最短路径--Bellman-Ford算法

一.最小生成树

1.1概念

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树就不在连通；反之，在其中引入任何一条新边，都会形成一条回路。

若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。

1. 只能使用图中的边来构造最小生成树

2. 只能使用恰好n-1条边来连接图中的n个顶点

3. 选用的n-1条边不能构成回路

1.2Kruskal算法

思路：先构造n个顶点的，不含边的图（G={V,NULL}），后面不断从边的集合中选出权值最小的那一条边，并且加入该边后不会形成回路。

核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树

例如：

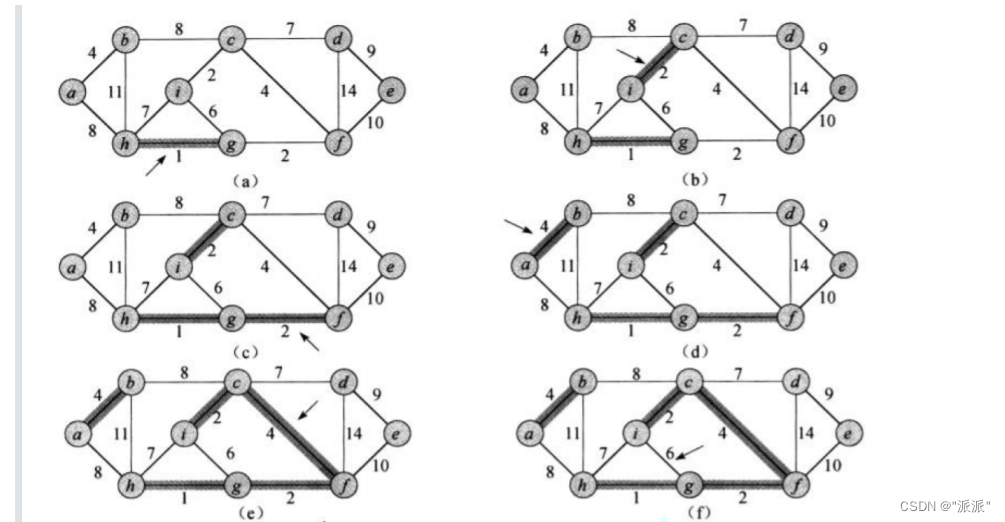
步骤：

1.先构造n个顶点，无边的图。

2.将原来图的边存储好，放入一个可排序的容器中，例如priority_queue,将边按权值的大小排好序。

3.后面选出权值最小的边时，将其加入图中，此时要知道该边的两个顶点与权值。所以priority_queue存储的是边的权值以及该边两边的顶点信息，可用一个结构体来表示。

4.每次选出权值最小的边时，将其加入图中时，要判断加入的边是否会形成回路，可用并查集来判断。

5.选出n-1条边，且未形成回路，即是最小生成树

代码实现：

 struct Edge   //优先级队列存储的元素{int _dsti;  //起始点下标int  _srci;// 目标点的下标W _w;		// 权值Edge(int srci,int dsti, const W w):_dsti(dsti), _srci(srci), _w(w){}bool operator>(const Edge& e) const //从小到大排列{return _w > e._w;}};typedef Grap<V, W, W_MAX, Direc> Self;W Kruskal(Self minTree){int n = _vertexs.size();for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, W_MAX);}priority_queue<Edge, vector<Edge>, greater<Edge>> _q; //先将边存储到的队列排好序for (int i = 0; i < n; i++){for (int j = 0; j < n; j++){if (_matrix[i][j] != 0)_q.push(Edge(i, j, _matrix[i][j]));}}cout << "开始选边" << endl;UnionFindSet u(n);  //并查集int k = 0;W sum=W();while (!_q.empty()){Edge e = _q.top();_q.pop();if (!u.InSet(e._dsti, e._srci)) //若位形成回路{cout << "选出" << _vertexs[e._dsti]<<" " <<_vertexs[e._srci]<<" "<< e._w << endl;u.Union(e._dsti, e._srci);sum += e._w;minTree.AddEdge(_vertexs[e._dsti], _vertexs[e._srci], e._w);k++;}}if (k = n - 1){return sum;}else{cout << "存在回路" << endl;}}

结果：创建的是上面的图

void test1()
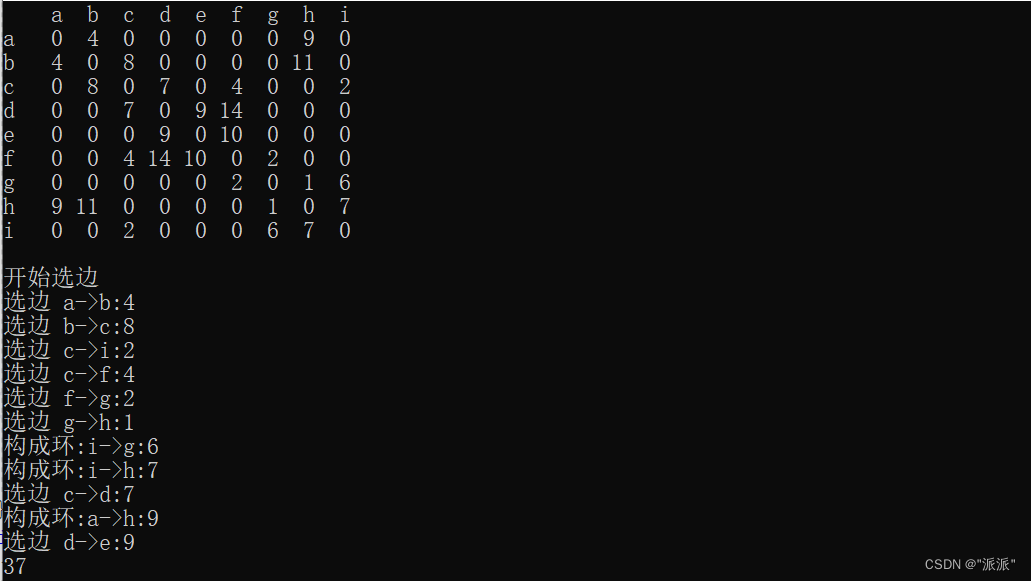
{const char* str = "abcdefghi";Grap<char, int> g(str, strlen(str));g.AddEdge('a', 'b', 4);g.AddEdge('a', 'h', 8);g.AddEdge('a', 'h', 9);g.AddEdge('b', 'c', 8);g.AddEdge('b', 'h', 11);g.AddEdge('c', 'i', 2);g.AddEdge('c', 'f', 4);g.AddEdge('c', 'd', 7);g.AddEdge('d', 'f', 14);g.AddEdge('d', 'e', 9);g.AddEdge('e', 'f', 10);g.AddEdge('f', 'g', 2);g.AddEdge('g', 'h', 1);g.AddEdge('g', 'i', 6);g.AddEdge('h', 'i', 7);g.Print();cout << g.Kruskal(g) << endl;}

1.3Prim算法

思路：从任意一个顶点开始，选出与其相连且权值最小的边，后面已经遍历过的顶点进行同样的操作，直到选完n-1条边。（选过的边不在遍历，该算法是贪心思想）

例如：假如从顶点A开始选边

步骤

1.先构造n个顶点，无边的图。

2.从给出的顶点（a）开始，将其与其相连的边放入优先级队列中排序，选出权值最小的边。同时记录该边对应的另一个顶点(b)。（此时顶点a已访问过，在添加边时，后面选出的边中对应的另一个顶点不能是a,在将对应顶点相连的边加入队列时，选出的边中顶点也必须是未访问过的，才能不形成回路）

3.对顶点b进行上面步骤2操作

3.选出n-1条边，且未形成回路，即是最小生成树。

代码：

  W Prim(Self minTree, const W& src)
{size_t srci = get_index(src);size_t n = _vertexs.size();minTree._matrix.resize(n);for (size_t i = 0; i < n; ++i){minTree._matrix[i].resize(n, 0);}vector<bool> X(n, true);vector<bool> Y(n, true);X[srci] = false; //从X集合中选出到集合Y的最短边Y[srci] = false;priority_queue<Edge, vector<Edge>, greater<Edge>> minq;for (size_t i = 0; i < n; ++i)// 先把起始点连接的边添加到队列中{if (_matrix[srci][i] != 0){minq.push(Edge(srci, i, _matrix[srci][i]));}}cout << "开始选边" << endl;size_t size = 0;W totalW = W();while (!minq.empty()){Edge min = minq.top();minq.pop();// 最小边的目标点也在X集合，则构成环,不要添加if (!X[min._dsti]){cout << "构成环:";cout << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;}else{minTree._AddEdge(min._srci, min._dsti, min._w);cout << "选边" << " " << _vertexs[min._srci] << "->" << _vertexs[min._dsti] << ":" << min._w << endl;X[min._dsti] = false;Y[min._dsti] = false;++size;totalW += min._w;if (size == n - 1)break;for (size_t i = 0; i < n; ++i){if (_matrix[min._dsti][i] != 0 && Y[i])// 顶点i是未访问过的{minq.push(Edge(min._dsti, i, _matrix[min._dsti][i]));}}}}if (size == n - 1){return totalW;}else{return W();}
}

结果：

二.最短路径

最短路径问题：从在带权有向图G中的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总和达到最小。

2.11单源最短路径--Dijkstra算法

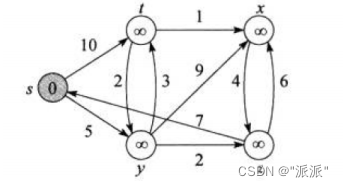
介绍：Dijkstra算法就适用于解决带权重的有向图上的单源最短路径问题，同时算法要求图中所有边的权重非负。一般在求解最短路径的时候都是已知一个起点和一个终点，所以使用Dijkstra算法求解过后也就得到了所需起点到终点的最短路径。

思路：

针对一个带权有向图G，将所有结点分为两组S和Q，S是已经确定最短路径的结点集合，在初始时为空（初始时就可以将源节点s放入，毕竟源节点到自己的代价是0），Q 为其余未确定最短路径的结点集合，每次从Q 中找出一个起点到该结点代价最小的结点u ，将u 从Q 中移出，并放入S中，对u 的每一个相邻结点v 进行松弛操作。松弛即对每一个相邻结点v ，判断源节点s到结点u的代价与u 到v 的代价之和是否比原来s 到v 的代价更小，若代价比原来小则要将s 到v 的代价更新为s 到u 与u 到v 的代价之和，否则维持原样。

例如：一下面这幅图为例

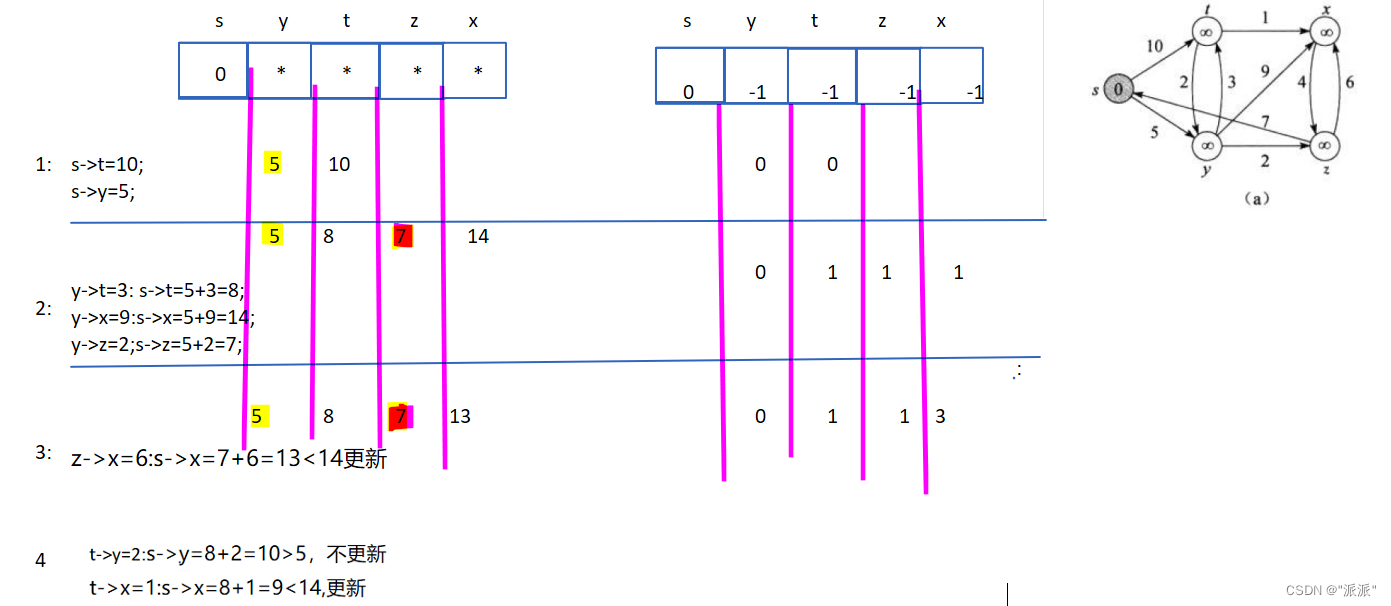
上面的两个数组中，一个来表示s->到目标点的最小权值，另一个来表示路径。简单来看，也就是贪心的思路，由s点出发，首先是s->y=5，所以s->y的最短路劲已确定。后面比较权值大小，从y开始找边，可确定s->z的最短路径为7。后面再比较权值大小，从t开始找边，确定s->x最短路径为8.后面以此类推。

代码：

void Dijkstra(const V& src, vector<W>& dist, vector<int>& pPath)
{size_t srci = get_index(src);size_t n = _vertexs.size();dist.resize(n, MAX_W);pPath.resize(n, -1);dist[srci] = 0;pPath[srci] = srci;// 已经确定最短路径的顶点集合vector<bool> S(n, true);for (size_t j = 0; j < n; ++j){int u = 0;W min = W_MAX;for (size_t i = 0; i < n; ++i) //选出s->目标点最小权值的那个，从它开始找边{if (S[i] == true && dist[i] < min){u = i;min = dist[i];}}S[u] = false; //已确定s->u的最短路径for (size_t v = 0; v < n; ++v)// 松弛更新u连接顶点v  srci->u + u->v <  srci->v  更新{if (S[v] == true && _matrix[u][v] != W_MAX&& dist[u] + _matrix[u][v] < dist[v]){dist[v] = dist[u] + _matrix[u][v];pPath[v] = u;}}}
}

打印路径： pPath数组中的下标表示表示对应的顶点，存储的值表示上一个联通它的顶点下标。

void PrintShortPath(const V& src, const vector<W>& dist, const vector<int>& pPath){size_t srci = get_index(src);size_t n = _vertexs.size();for (size_t i = 0; i < n; ++i){if (i != srci){// 找出i顶点的路径vector<int> path;size_t parenti = i;while (parenti != srci){path.push_back(parenti);parenti = pPath[parenti];}path.push_back(srci);reverse(path.begin(), path.end());//需要逆置下for (auto index : path){cout << _vertexs[index] << "->";}cout << dist[i] << endl;}}}

结果：

补充：该算法不能用于权值为负数的情况，当从一个顶点（A）到另一个顶点（B) 确定最短路径时，若有其它边是负数，则A->B的路径不一定是最短路径。

2.1.2单源最短路径--Bellman-Ford算法

bellman—ford算法可以解决负权图的单源最短路径问题，思路是暴力去遍历所有的边，由于存在负权的边，所以遍历完一次所有的边后，还要再去遍历n-1次，去更新负权边的影响。

例如：

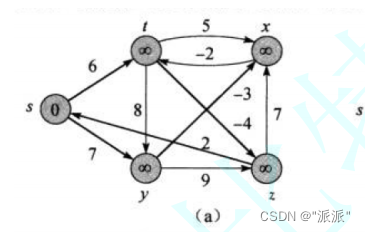
当从s去遍历时，并不能确定s->t=6是最短路径，s->y->x->t比从s->t的权值还要小，原因就是存在带负权的边。当遍历完与s相连的边后，暂且确定了s->t，s->y的最短路径。再去遍历与t，y相连的边，确定t->x,t->y，t->z的最短路径，进而确定s->x，s->y，s->z的路径......。当遍历到有负权的边时，与该边相连点（假设为m）s->m的最短路劲可能变化。有n个顶点，所以要遍历n次。

代码：

	bool BellmanFord(const V& src, vector<W>& dist, vector<int>& pPath){size_t n = _vertexs.size();size_t srci = get_index(src);dist.resize(n, W_MAX);pPath.resize(n, -1);dist[srci] =0;for (size_t k = 0; k < n; ++k)// 总体最多更新n轮{// i->j 更新松弛bool update = false;cout << "更新第:" << k << "轮" << endl;for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){//dist[i]表示的是 srci -> i 的权值if (_matrix[i][j] != 0 && dist[i] + _matrix[i][j] < dist[j]){update = true;dist[j] = dist[i] + _matrix[i][j];pPath[j] = i;}}}// 如果这个轮次中没有更新出更短路径，那么后续轮次就不需要再走了if (update == false){break;}}return true;}

如果存在带负权的回路呢？例如：

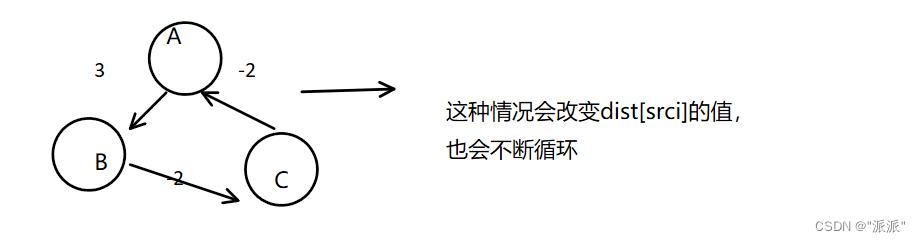
只需判断一下即可

if (j != srci)
{if (_matrix[i][j] != 0 && dist[i] + _matrix[i][j] < dist[j]){update = true;cout << _vertexs[i] << "->" << _vertexs[j] << ":" << _matrix[i][j] << endl;dist[j] = dist[i] + _matrix[i][j];pPath[j] = i;}
}

但下面这种情况：

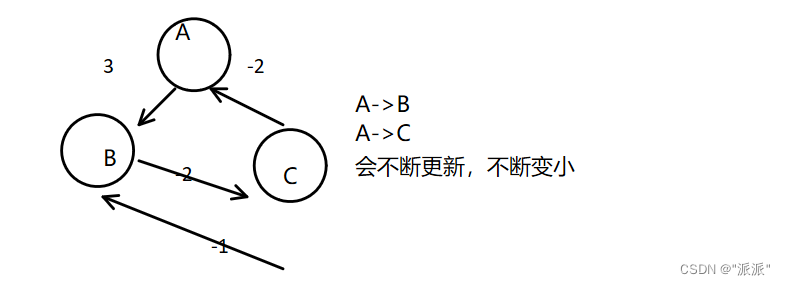
在遍历n次后进行判断，若还能更新，即存在负权回路；

	for (size_t i = 0; i < n; ++i){for (size_t j = 0; j < n; ++j){// srci -> i + i ->jif(j!=srci){if (_matrix[i][j] != 0 && dist[i] + _matrix[i][j] < dist[j]){cout << "带负权回路" << endl;return false;}}}}return true;}

代码测试：

void test2()
{const char* str = "syztx";Grap<char, int,INT_MAX, true> g(str, strlen(str));g.AddEdge('s', 't', 10);g.AddEdge('s', 'y', 5);g.AddEdge('y', 't', 3);g.AddEdge('y', 'x', 9);g.AddEdge('y', 'z', 2);g.AddEdge('z', 's', 7);g.AddEdge('z', 'x', 6);g.AddEdge('t', 'y', 2);g.AddEdge('t', 'x', 1);g.AddEdge('x', 'z', 4);g.Print();vector<int> dist;vector<int> parentPath;g.BellmanFord('s', dist, parentPath);cout << "打印路径" << endl;g.PrintShortPath('s', dist, parentPath);
}

结果：