什么是线性表:
线性表是有限的数据元素组成的有限序列。
通常用(a1,a2,a3…,an),来表示
线性表的两种存储结构:
1.顺序存储结构(数组);
2.链式存储结构(链表);
数据结构-线性表
- 一、线性表的ADT定义
- 二、顺序存储结构
- 三、链式存储结构
- 四、顺序表与链式表比较
一、线性表的ADT定义
ADT SeqList{
数据对象:D = {ai|ai∈ElemSet,i=1,2,…,n,n≥0}
数据关系:R = {<ai-1,ai>| ai-1,ai∈D,i=2,…,n}
基本操作:InitSeqList(&L)操作结果:构造一个空的线性表L。DestroySeqList(&L)初始条件:线性表L已存在。操作结果:销毁线性表L。ClearList(&L)初始条件:线性表L已存在。操作结果:将L重置为空表。ListEmpty(&L)初始条件:线性表L已存在。操作结果:若L为空表,则返回true,否则返回false。ListLength(&L)初始条件:线性表L已存在。操作结果:返回L中数据元素个数。GetElem(L,i,&e)初始条件:线性表L已存在,且1<=i<=ListLength(L)。操作结果:用e返回L中第i个数据元素的值。LocateElem(L,e)初始条件:线性表L已存在。操作结果:返回L中第1个值与e相同的元素在L中的位置。若这样的数据元素不存在,则返回值为0。 PriorElem(L,cur_e,&pre_e)初始条件:线性表L已存在。操作结果:若cur_e是L的数据元素,且不是最后一个,则用pre_e返回其前驱,否则操作失败,pre_e无定义。NextElem(L,cur_e,&next_e)初始条件:线性表L已存在。操作结果:若cur_e是L的数据元素,且不是最后一个,则用next_e返回其后继,否则操作失败,next_e无定义。ListInsert(&L,i,e)初始条件:线性表L已存在,且1<=i<=ListLength(L)+1。操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1。 ListDelete(&L,i)初始条件:线性表L已存在且非空,且1<=i<=ListLength(L)。操作结果:删除L的第i个数据元素,L的长度减1。TraverList(L)初始条件:线性表L已存在。操作结果:对线性表L进行遍历,在遍历过程中对L的每个节点访问一次。
} ADT SeqList
代码实现:
/*
seqlist.h 顺序表
*/#define MAXSIZE 100 //最大的元素个数typedef int ElemType; //定义元素类型enum Status{Ok,Error}; //枚举类型的状态,表示成功或失败typedef struct
{ElemType *elem; //指针,存储空间动态申请int length; //线性表的长度
}SeqList;Status InitSeqList(SeqList &L); //顺序表的初始化
Status SeqListInsert(SeqList &L, int i, ElemType e); //插入操作
Status SeqListDelete(SeqList &L, int i); //删除元素
void TraverseSeqList(SeqList L); //遍历顺序表
Status ListEmpty(SeqList &L); //线性表是否为空
Status ClearList(SeqList &L); //将L重置为空表
Status DestroySeqList(SeqList &L); //销毁线性表
Status GetElem(SeqList &L,int i,ElemType &e); //用e返回L中第i个数据元素的值
int LocateElem(SeqList &L,ElemType &e); //查询数据的位置
Status PriorElem(SeqList &L, ElemType cur_e, ElemType &pre_e); //当前元素cur_e不是第一个数据,就pre_e返回它的前一个数据的值,否则返回error
Status NextElem(SeqList &L, ElemType cur_e, ElemType &next_e); //当前元素不会最后一个,就用next_e返回它的后一个数值,否则返回error顺序表的初始化
/*seqlist.cpp 顺序表实现
*/
#include <iostream>
#include <stdio.h>
#include "seqlist.h"
using namespace std;//顺序表的初始化
Status InitSeqList(SeqList &L)
{ //构建一个空的顺序表L.elem = new ElemType[MAXSIZE]; //申请内存空间if(!L.elem){ //判断是否申请成功cout<<"create failed!!!"<<endl;return Error;}L.length = 0; //初始化长度为0return Ok;
}
插入元素
//在顺序表L的i位置,插入元素e
Status SeqListInsert(SeqList &L, int i, ElemType e)
{//在顺序表L的中的第i个位置,插入新元素e,i值的合法范围是1≤i≤L.length+10if((i < 1) || (i > L.length + 10)) //判定i位置是否合法{cout<<"i位置非法"<<endl;return Error;}if(L.length == MAXSIZE) //当前顺序表存储空间已满{cout<<"当前顺序表存储空间已满"<<endl;return Error;}for(int j=L.length-1;j>=i-1;j--) //插入的位置及后面的元素都向后移一位{L.elem[j+1] = L.elem[j];}L.elem[i-1] = e; //将新元素放在第i位置L.length++; //顺序表长度+1return Ok;
}
删除元素
//删除位置i处的元素
Status SeqListDelete(SeqList &L, int i){//位置合法性if(i<1||i>L.length){cout<<"i位置不合法"<<endl;return Error;}//i后的元素向前移动一位for(int j=i;j<L.length;j++){L.elem[j-1] = L.elem[j];}L.length--;return Ok;
}
遍历表
//遍历顺序表
void TraverseSeqList(SeqList L){if(L.length==0){cout<<"\n顺序表为空!"<<endl;}for(int i=0;i<L.length;i++){cout<<L.elem[i]<<" ";}cout<<endl;
}
清空表
//清空线性表中的数据
Status ClearList(SeqList &L){if(L.length == 0){cout<<"\n线性表为空\n"<<endl;return Error;}for (int j = 0; j < L.length; j++){L.elem[j] = 0;}L.length = 0;cout<<"\n已清空线性表\n"<<endl;return Ok;
}
释放线性表内存
//销毁线性表
Status DestroySeqList(SeqList &L){if(!L.elem){cout<<"线性表不存在"<<endl;return Error;}free(L.elem);L.elem = NULL;cout<<"\n线性表已销毁\n"<<endl;return Ok;
}
返回某个位置的值
//用e返回L中第i个数据元素的值
Status GetElem(SeqList &L,int i,ElemType &e){if(i > L.length || i < 1){cout<<"i的位置不合法"<<endl;return Error;}else{e = L.elem[i-1];return Ok;}
}
返回某个元素在表中的位置
///返回与元素e相同的元素在线性表中的位置
int LocateElem(SeqList &L,ElemType &e)
{//在顺序表中查找值为e的元素,返回其位置int currentIndex = -1;if(L.length == 0){cout<<"当前线性表为空"<<endl;return currentIndex;}for(int i = 0;i < L.length;i++){if(L.elem[i] == e){currentIndex = i+1;break;}}if(currentIndex == -1){cout<<"数据 "<<e<<" 不存在当前线性表中"<<endl;}return currentIndex;
}
返回前驱
//如果元素e不是第一个值,就用pre_e返回cur_e前一个的值(前驱)
Status PriorElem(SeqList &L, ElemType cur_e, ElemType &pre_e)
{//查找元素e所在的位置int temp = LocateElem(L,cur_e);if(temp == -1){return Error;}if(temp - 1 == 0){cout<<"该元素不存在直接前驱"<<endl; return Error;}else{pre_e = L.elem[temp - 2];return Ok;}
}
返回后继
//如果元素e不是最后一个的值,就用next_e返回cur_e后一个值(后继)
Status NextElem(SeqList &L, ElemType cur_e, ElemType &next_e)
{//查找元素e所在的位置int temp = LocateElem(L,cur_e);if(temp == -1){return Error; }if(temp == L.length){cout<<"该数据不存在直接后继"<<endl;return Error;}else{next_e = L.elem[temp];return Ok;}
}
二、顺序存储结构
线性表的顺序存储是指用一组连续的存储单元依次存储线性表中的数据元素,从而使得逻辑上相邻的两个元素在物理存储位置上也相邻。这种存储方式无需占用额外的存储空间来存储。
优点:
1.查找数据元素时的时间复杂度都是O(1)。
2.无需为数据元素之间的逻辑关系而耗费新的空间。
缺点:
1.在进行增加元素、删除元素时、时间复杂度时O(n),不方便数据元素的增删。
2.需要在创建时确定长度,在实际项目中很多时候在一开始很难确定线性表的大小。
3.需要占用整块连续的内存空间,容易造成存储空间的碎片化。
三、链式存储结构
链式表由节点node组成,一个node就是一个数据,也就是一个数据节点,每个节点由数据域和指针域构成,数据域用来存放数据,而指针域用来指定下一个目标节点。
单链表:最后一个节点指针域为null
循环链表:最后一个指针域为指向第一个节点。因此循环链表可以从任意节点开始遍历整个链表。
双向链表:每个节点包含两个指针,分别指明当前元素的直接前驱和直接后继的存储信息。可以从两个方向遍历链表中的元素。
四、顺序表与链式表比较
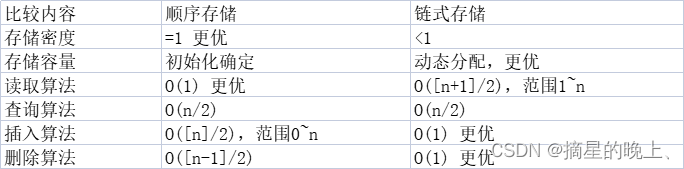
参考资料:数据结构与算法基础课程-王卓老师