分割依据的灰度值基本性质是：不连续性和相似性。本章中的大多数分割算法均基于灰度值的两个基本性质。第一类方法根据 灰度的突变，如 边缘 将图像分割为多个区域；第二类方法根据一组 预定义的准则 将图像分割为多个区域 。 阈值处理、区域生长、区域分离和聚合都是这类方法的例子 。

10.2 点、线和边缘检测

图像特征：孤立点、线和边缘。

10.2.2 孤立点的检测

点检测应以二阶导数为基础。使用的拉普拉斯核(它与图3.45(b)中的核相同)，若滤波器在这一点的响应的绝对值超过一个规定的阈值，则我们说在核的中心位置 $(x,y)$ 检测到了一个点。

10.2.3 线检测

复杂度更高的检测是线检测。 对于线检测， 也可使用图10.4(a)中的拉普拉斯核， 但必须正确处理二阶导数的双线效应。

10.2.4 边缘模型

三类边缘模型：台阶、斜坡、屋顶边缘模型

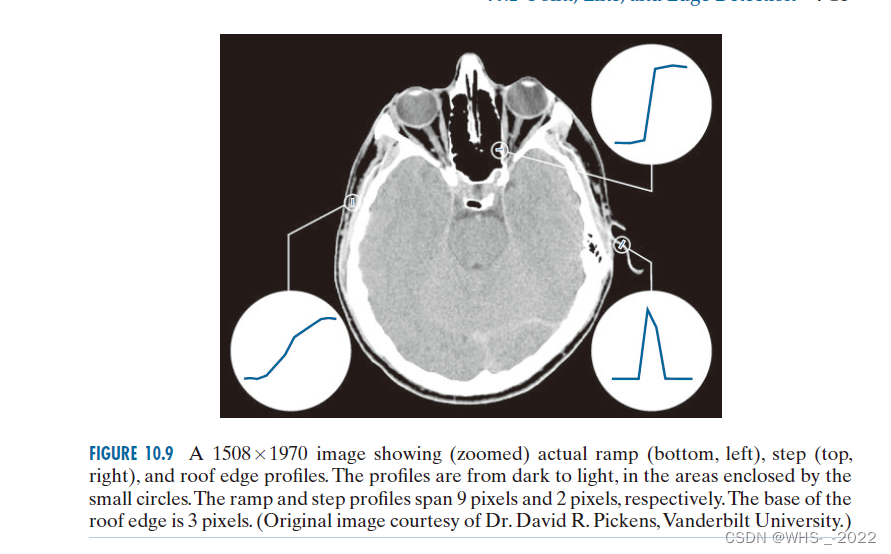
微弱的可见噪声严重影响检测边缘所用的两个 关键导数。

边缘检测的步骤：

1. 为了降低噪声，对图像进行 平滑处理 。

2. 检测边缘点。从图像中提取可能是边缘点的所有点 候选边缘点 。

3. 边缘定位。目的是 从候选边缘点中选择组成边缘的点集中的成员点 。

10.3 阈值处理

由于图像阈值处理直观、 实现简单且计算速度快， 因此在图像分割应用中处于核心地位。

从背景中提取目标的一种明显方法是， 选择一个分隔这些模式的阈值 $T$。 然后， 图像中 $f(x,y)>T$ 的任何点 $(x,y)$， 称为一个目标点； 否则，该点称为背景点。 换句话说，分割后的图像 $g(x,y)$ 为：

$$g(x,y)=\{\begin{array}{l}1,f(x,y)>T\\ \\ 0,f(x,y)\le T\end{array}\text{\hspace{1em}(10.46)}$$

当T是一个适用于整个图像的常数时， 式(10.46)给出的处理称为全局阈值处理。 当 $T$ 值在一幅图像上变化时， 称为可变阈值处理。

灰度阈值处理能否成功， 与分隔直方图模式的波谷的宽度和深度有关。

噪声

噪声污染较强的情况下，没有希望为分割图像找到一个合适的阈值。

光照和反射

图10.34(f)是光照不均匀图像(c)的直方图，可见：波峰之间的深谷会破坏到模式无法分割的程度。 如果光照非常均匀， 但(目标和/或背景表面自然反射率的变化导致的)图像反射不均匀， 也会得到类似结果。

在使用阈值或其他分割技术分割图像时，光照和反射起核心作用。

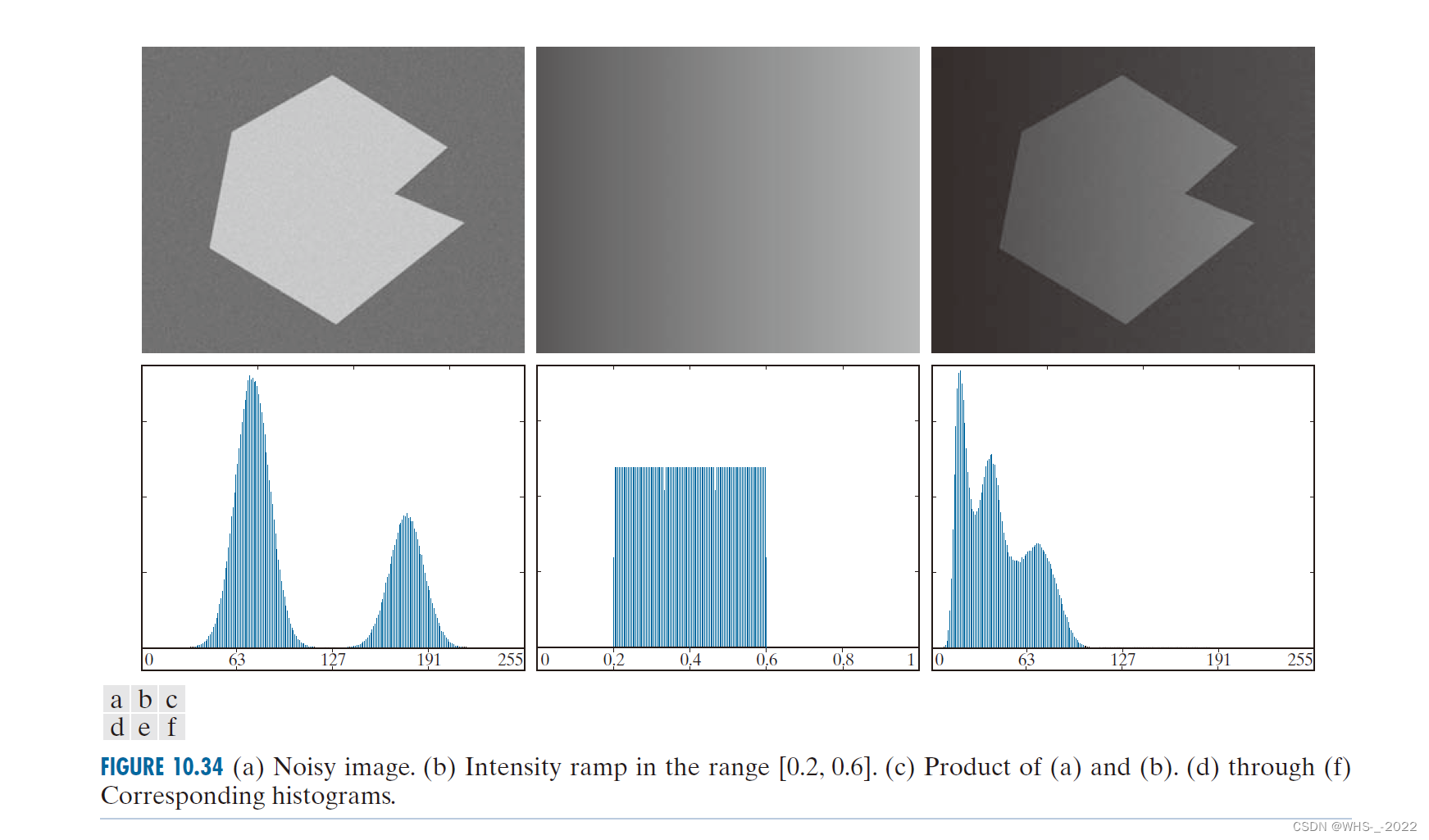
基本的全局阈值处理

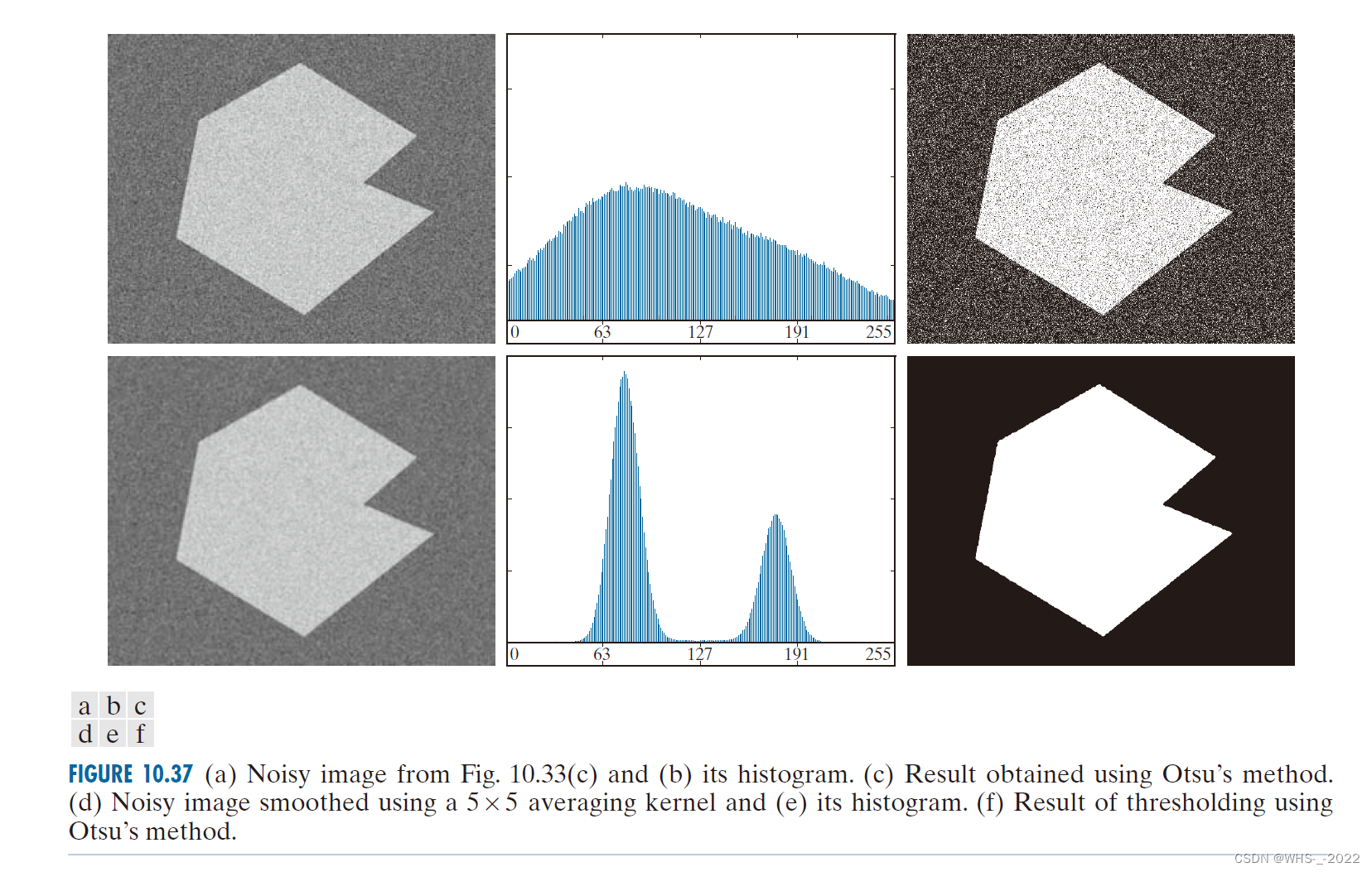
10.3.4 使用图像平滑改进全局阈值处理

如图10.33所示， 噪声会使得简单的阈值处理问题变得不可求解。当无法从源头降低噪声， 并且阈值处理是首选分割方法时， 增强分割性能的一种技术通常是：在阈值处理之前先平滑图像。

10.3.5 使用边缘改进全局阈值处理

若只利用位于或接近目标和背景间的边缘的像素， 则得到的直方图将有几个高度近似相同的波峰。 此外， 任何位于目标上的像素的概率， 将近似等于其位于背景上的概率， 从而改进了直方图模式的对称性。

使用满足某些基于梯度和拉普拉斯的简单测度的像素， 有加深直方图波峰间的波谷的倾向。

10.4 使用区域生长、区域分离与聚合进行分割

区域生长、区域分离与聚合。