多数之和问题

news/2024/11/8 0:41:07/

文章目录

  • 多数求和问题
  • 1两数之和(无序)
    • 题解
  • 2两数之和(有序)
    • 题解
  • 3两数之和(二叉搜索树)
    • 题解
  • 4 三数之和
    • 题解
  • 5四数之和
    • 题解

多数求和问题

针对给一组用例,和一个目标数target,求用例中多数相加等于target的所有数,且不能重复问题,一般有两种解法:

  • 集合(不要求排序)
  • 双指针(要求排序);

利用集合一般求解两数之和问题,时间复杂度达到O(n);

而双指针问题可以把N数之和问题从时间复杂度O(Nn)降低到O(N(n-1));

此两种解法的具体思路在第一题和第二题分别会进行详细叙述,后面的题便直接使用,不再赘述

1两数之和(无序)

链接

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

题解

如果 a + b = target,当我们从头开始遍历数组碰到a(或者b)时,b(或者a)一定在a(或者b)后面,那么我们每遍历一个数a,就先检查集合中是否存在target-a,如果有,返回结果 ; 如果没有,则将a添加进集合,当后面碰到b时候,a肯定已经在集合里面,可以查找到结果,整个时间复杂度为O()

下面以数组[3,5,4,7,6,2,11,8],target=16为例,进行演示过程:

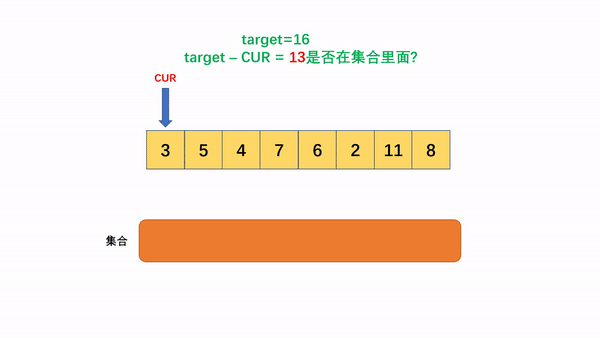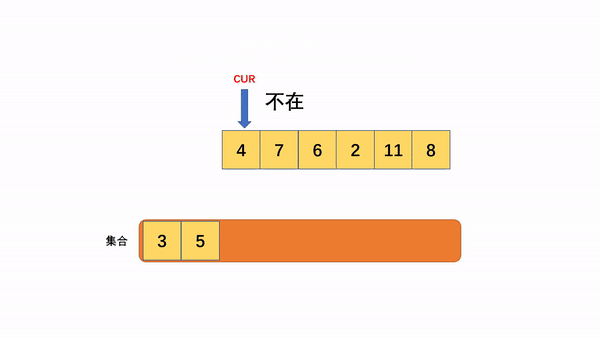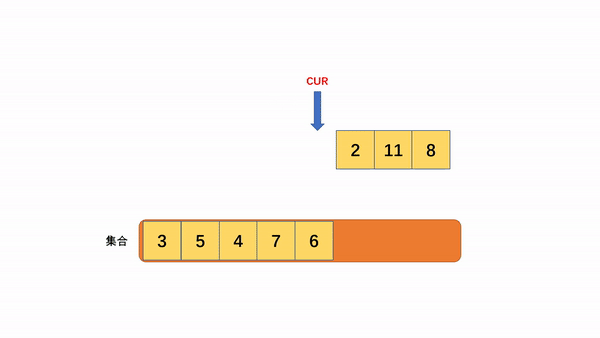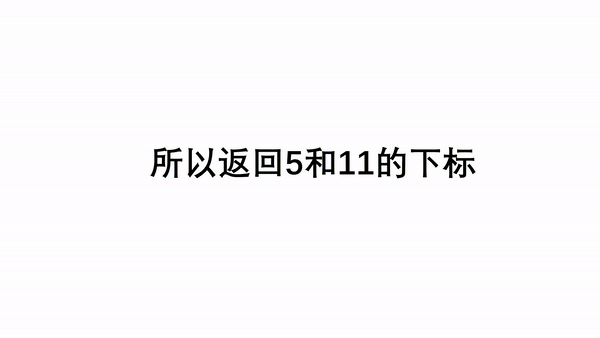
在这里插入图片描述

不过此题是要求写索引,所以我们用map将值和索引进行映射;

vector<int> twoSum(vector<int>& nums, int target) {unordered_map<int,int> umap;    //用来映射值和索引for(int i = 0;i<nums.size();i++){auto ret = umap.find(target - nums[i]);  //先检查target-nums[i]的值是否在集合里面if(ret != umap.end()){                   //如果在,就返回正确结果return {ret->second,i};              }umap[nums[i]] = i;                      //如果不在,就将CUR值放进集合}return {};
}

2两数之和(有序)

链接

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

示例 1：

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]
解释：2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

示例 2：

输入：numbers = [2,3,4], target = 6
输出：[1,3]
解释：2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。

示例 3：

输入：numbers = [-1,0], target = -1
输出：[1,2]
解释：-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。

题解

此题有序,我们可以采用双指针解法,即一开始left指向最左边,right指向最右边,那么

  • 当nums[left]+ nums[right] > target时候,那么其中一个目标值一定不是nums[right],所以right应该左移
  • 当nums[left]+ nums[right] < target时候,那么其中一个目标值一定不是nums[left],所以left应该右移

最终便一定可以找到目标值

以数组[1,3,4,7,8,13,18,21,23,26],target=20为例,看下图:

在这里插入图片描述

    vector<int> twoSum(vector<int>& numbers, int target) {int low = 0, high = numbers.size() - 1;while (low < high) {int sum = numbers[low] + numbers[high];if (sum == target) {return {low + 1, high + 1};} else if (sum < target) {++low;} else {--high;}}return {-1, -1};}

3两数之和(二叉搜索树)

链接

给定一个二叉搜索树 root 和一个目标结果 k，如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果，则返回 true。
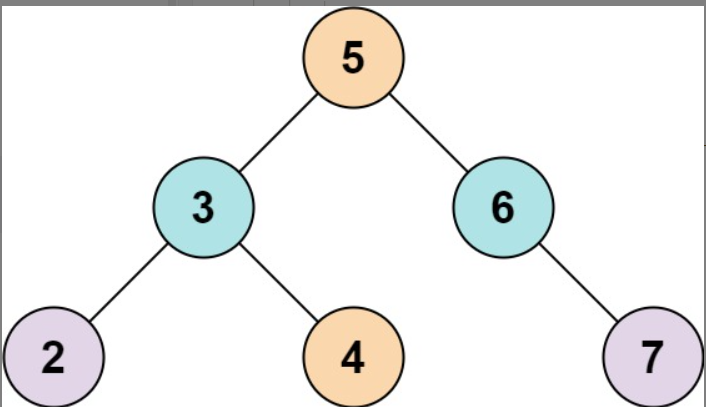
在这里插入图片描述

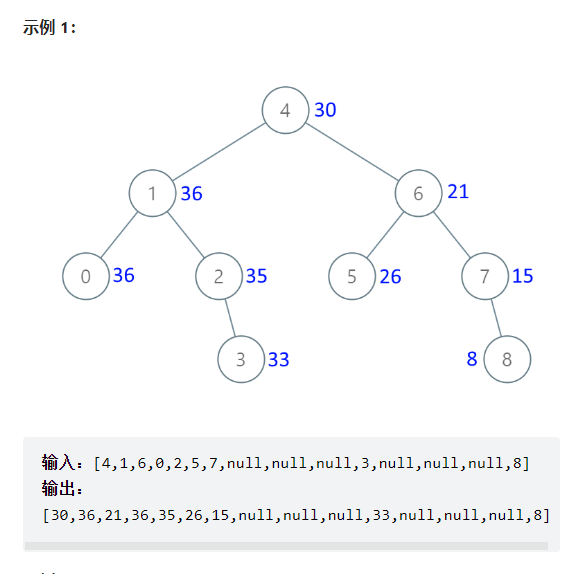
示例 1：

输入: root = [5,3,6,2,4,null,7], k = 9
输出: true

示例 2：

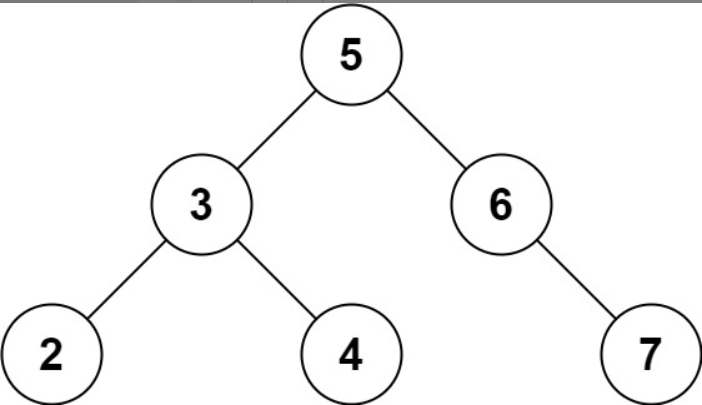
在这里插入图片描述

输入: root = [5,3,6,2,4,null,7], k = 28
输出: false

题解

此题是一个二叉搜索树,其本质两数之和(无序)没有什么区别,都是在遍历当前结点时候,检查集合是否存在target剪去当前结点值,如果有就返回结果,如果没有,就存下当前值,因此当下一次遍历到target剪去之前值时候,就一定会存在集合中;

class Solution {
public:unordered_set<int> hashTable;bool findTarget(TreeNode *root, int k) {if (root == nullptr) {    //如果集合本身为空,说明不存在return false;}if (hashTable.count(k - root->val)) {     //检查target-当前值是否存在集合return true;}hashTable.insert(root->val);         //如果不存在就加入集合return findTarget(root->left, k) || findTarget(root->right, k);        //然后分别去左右子树检查结果}
};

4 三数之和

链接

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足i != j、i != k 且 j != k，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

题解

此题并没有太高级的算法,本质其实是暴力解,不过却可以利用双指针将时间 复杂度从O(n3)降低到O(n2),因为双指针分别从两边向中间走,本该两次的事情,却一次达到了;

此题怎么使用双指针呢?

首先进行排序,然后让第二层循环和第三层循环分别进行双指针算法,第一层进行遍历;

在这里插入图片描述

当然此题涉及比较多的数字之和,就需要考虑一些特殊情况了,比如数字全部一样[0,0,0,0,0,0,0,0,0,0,0],target = 0,那么怎么进行去重结果呢?

答案很简单,分别满足连个条件:

  • 索引First<Second<Third
  • 每一层访问的数字和其上一次访问的不一样,注意哦,这里说的是 层
    vector<vector<int>> threeSum(vector<int>& nums) {sort(nums.begin(),nums.end());      //排序vector<vector<int>> ret;            //存储结果for(int first = 0;first<nums.size()-2;first++){   //第一层循环,即图中的指针Fif(nums[first] > 0) break;		//因为已经排好序,如果第一个数就大于0,那么后面所有数字相加都不可能有等于0//第一层访问的数字不能和该层上一次访问的数字一样,有个条件first>0是因为该层第一次访问时,上一次没有可访问的数字if(first && nums[first] == nums[first-1]) continue;int second = first+1;   int third = nums.size()-1;while(second<third){   //双指针算法int tmp = nums[first] + nums[second] + nums[third];if(tmp == 0){ret.push_back({nums[first],nums[second],nums[third]});//第二层访问的数字不能和该层上一次访问的数字一样while(second < third && nums[second]==nums[second+1]) second++;   //第三层访问的数字不能该层上一次访问的数字一样while(second < third && nums[third]==nums[third-1]) third--;//如果找到结果了,双指针同时向中间走second++;third--;}else if(tmp > 0){   //如果结果集大于target,第二个指针向右走third--;}else{            //如果结果集小于target,第三个指针向左走second++;}}}return ret;}

5四数之和

给你一个由 n 个整数组成的数组 nums ，和一个目标值 target 。请你找出并返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] （若两个四元组元素一一对应，则认为两个四元组重复）：

0 <= a, b, c, d < n
a、b、c 和 d 互不相同
nums[a] + nums[b] + nums[c] + nums[d] == target
你可以按 任意顺序 返回答案 。

示例 1：

输入：nums = [1,0,-1,0,-2,2], target = 0
输出：[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]

示例 2：

输入：nums = [2,2,2,2,2], target = 8
输出：[[2,2,2,2]]

题解

此题没有什么好在画图的必要和解释了,和第四题本质一样,只是多了个循环而已,直接上代码

(代码中用long long代替是因为出题人的样例有点恶心,明明考算法,却弄了个整型溢出)

    vector<vector<int>> fourSum(vector<int>& nums, int target) {if(nums.size() < 4){return {};}long long target1 = target;sort(nums.begin(),nums.end());vector<vector<int>> ret;for(int first = 0;first<nums.size()-3;first++){if(first && nums[first] == nums[first-1]) continue;for(int second = first+1;second<nums.size()-2;second++){if(second > first+1 && nums[second] == nums[second-1]) continue;int third = second+1;int fourth = nums.size()-1;while(third < fourth){long long tmp = (long long)nums[first] + (long long)nums[second] + (long long)nums[third] + (long long)nums[fourth];if(tmp == target1){ret.push_back({nums[first] , nums[second] , nums[third] , nums[fourth]});while(third<fourth && nums[third] == nums[third+1]) third++;while(third<fourth && nums[fourth] == nums[fourth-1]) fourth--;third++;fourth--;}else if(tmp > target1){fourth--;}else{third++;}}}}return ret;}

http://www.ppmy.cn/news/2112.html

相关文章

springboot基于Java的电影院售票与管理系统毕业设计源码011449

springboot基于Java的电影院售票与管理系统毕业设计源码011449

电影院售票与管理系统的设计与实现 摘 要 信息化社会内需要与之针对性的信息获取途径&#xff0c;但是途径的扩展基本上为人们所努力的方向&#xff0c;由于站在的角度存在偏差&#xff0c;人们经常能够获得不同类型信息&#xff0c;这也是技术最为难以攻克的课题。针对电影院售…
阅读更多...
JVM—双亲委派

JVM—双亲委派

文章目录什么是双亲委派&#xff1f;为什么要有双亲委派原理&#xff1f;破坏双亲委派的例子————————————————————————————————什么是双亲委派&#xff1f; ​ 就是我们写的java源文件到最终运行&#xff0c;必须要经过编译和类加载这两个阶段…
阅读更多...
Springboot企业资源管理信息系统kvonv计算机毕业设计-课程设计-期末作业-毕设程序代做

Springboot企业资源管理信息系统kvonv计算机毕业设计-课程设计-期末作业-毕设程序代做

Springboot企业资源管理信息系统kvonv计算机毕业设计-课程设计-期末作业-毕设程序代做 【免费赠送源码】Springboot企业资源管理信息系统kvonv计算机毕业设计-课程设计-期末作业-毕设程序代做本源码技术栈&#xff1a; 项目架构&#xff1a;B/S架构 开发语言&#xff1a;Java…
阅读更多...
TCP--三次握手和四次挥手

TCP--三次握手和四次挥手

原文网址&#xff1a;TCP--三次握手和四次挥手_IT利刃出鞘的博客-CSDN博客 简介 本文介绍TCP的三次握手和四次挥手。即&#xff1a;TCP建立连接和断开连接的过程。 三次握手 流程图 主机 A为客户端&#xff0c;主机B为服务端。 第一次握手 A 发送同步报文段&#xff08;SYN…
阅读更多...
一篇文章让你搞懂各种压缩，gzip压缩，nginx的gzip压缩，Minification压缩

一篇文章让你搞懂各种压缩，gzip压缩，nginx的gzip压缩，Minification压缩

前言 同学们可能听过这些压缩&#xff0c;但是可能不是了解&#xff0c;这篇文章让你弄清他们 webpack的gzip压缩和nginx的gzip压缩有什么区别&#xff1f;怎样开启gzip压缩&#xff1f;Minfication压缩又是什么鬼&#xff1f;怎样使项目优化的更好&#xff1f;本篇文章讲的是…
阅读更多...
TypeScript算法题实战——二叉搜索树篇

TypeScript算法题实战——二叉搜索树篇

二叉搜索树&#xff0c;也叫二叉查找树、二叉排序树&#xff0c;是具有下列性质的二叉树&#xff1a; 若它的左子树不空&#xff0c;则左子树上所有结点的值均小于它的根结点的值&#xff1b; 若它的右子树不空&#xff0c;则右子树上所有结点的值均大于它的根结点的值。 注意…
阅读更多...
C++校园导游程序及通信线路设计

C++校园导游程序及通信线路设计

C校园导游程序及通信线路设计 一、设计内容&#xff1a; 设计校园平面图&#xff0c;所含景点不少于10个。以图中顶点表示校内各景点&#xff0c;存放景点名称、代号、简介等信息&#xff1b;以边表示路径&#xff0c;存放路径长度等相关信息。 (1) 显示校园平面图&#xff08…
阅读更多...
RK3568平台开发系列讲解（音视频篇）如何把音视频流进行网络传输？

RK3568平台开发系列讲解（音视频篇）如何把音视频流进行网络传输？

🚀返回专栏总目录 文章目录 一、什么是RTP二、RTP 协议详解三、RTCP 协议详解沉淀、分享、成长，让自己和他人都能有所收获！😄 📢如何将码流打包成一个个数据包发送到网络上，那么我们就需要来了解一下 RTP 和 RTCP 协议。 一、什么是RTP 为了保证传输的实时性，一般使…
阅读更多...
最新文章

Copyright @ 2022~2023