一. 题目

1. 链接

题目链接：LeetCode: 812. 最大三角形面积

2. 框架

c++代码框架：

class Solution {
public:double largestTriangleArea(vector<vector<int>>& points) {}
};

3. 描述

  给定包含多个点的集合，从其中取三个点组成三角形，返回能组成的最大三角形的面积。

4. 示例

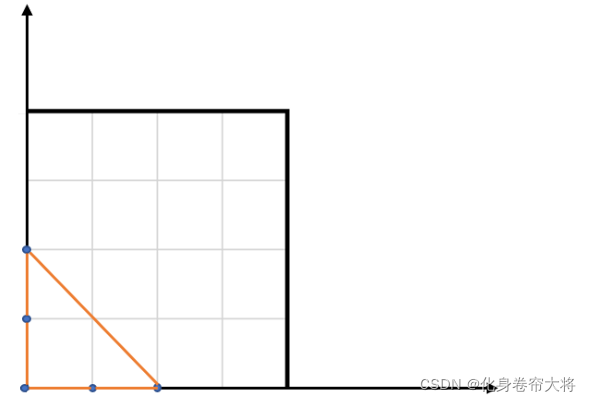
输入: points = [ [0,0], [0,1], [1,0], [0,2], [2,0] ]
输出: 2
解释:
这五个点如下图所示。组成的橙色三角形是最大的，面积为2。

5. 数据范围

   3 <= points.length <= 50.   (不存在重复的点)
 -50 <= points[i][j] <= 50.    (结果误差值在 10^-6 以内都认为是正确答案)

二. 解题

1. 思路

(1) 因为是没有重复的点存在，需要找到三个点计算三角形面积的方法，$S=(底\ast 高)/2$
(2) 因为范围不大，可以直接在集合中选三个点，求取面积记录最大值返回（网络上由很多种计算方式）

2. 复杂度

$O(n^3)$

3. 源码

class Solution {
public:double area(vector<int>& a, vector<int>& b, vector<int>& c) {return fabs( (b[0]-a[0]) * (c[1]-a[1]) - (b[1]-a[1]) * (c[0]-a[0]) ) / 2;}double largestTriangleArea(vector<vector<int>>& points) {int len = points.size();double res = 0;for (int i = 0; i < len - 2; i++) {for (int j = i + 1; j < len - 1; j++) {for (int k = j + 1; k < len; k++) {res = max(area(points[i], points[j], points[k]), res);}}}return res;}
};

4. 考察

三点计算三角形面积