编译原理 SLR(1) 语法分析器的构建

在我的博客查看：https://chenhaotian.top/study/compilation-principle-slr1/

实验三自底向上语法分析器的构建

项目代码：https://github.com/chen2438/zstu-study/tree/main/%E7%BC%96%E8%AF%91%E5%8E%9F%E7%90%86/%E5%AE%9E%E9%AA%8C/%E5%AE%9E%E9%AA%8C%E4%B8%89/

一、实验要求

运用SLR(1)或者LR(1)分析法，针对给定的上下文无关文法，给出实验方案。预估实验中可能出现的问题。

二、实验方案

（评价依据实验方案设计是否合理，包括输入输出的设计）

使用SLR(1)文法。逐步完成Augmented Grammar、First&Follow Set、DFA、Parse Table。

然后将分析表处理为程序可读数据，程序根据分析表的内容得出分析过程和结果。

输入设计：

Parse Table、Augmented Grammar。

输出设计：

带有Parsing Stack、Input和Action的分析过程。

三、预估问题

（是否有预估的问题，预估的问题是否合理）

程序需要事先获得Augmented Grammar、Parse Table、Terminals、Non-terminals的具体内容，这些数据都要被处理为适当的格式，过程比较繁琐。
可以将每个(non)terminal映射为数字，便于直接调用table(i,(non)terminal)。
注意非终结符id的特殊处理。

理论基础（评价依据理论知识非常清楚）

四、内容和步骤

1、考虑简单算术表达式文法G:

E→E + T | T
T→T * F | F
F→(E) | id

试设计SLR(1)或者LR(1)分析程序，以输入的 (a+b)*c+(d+e) 符号串进行语法分析。

2、实验具体步骤

实验三-1

实验三-2

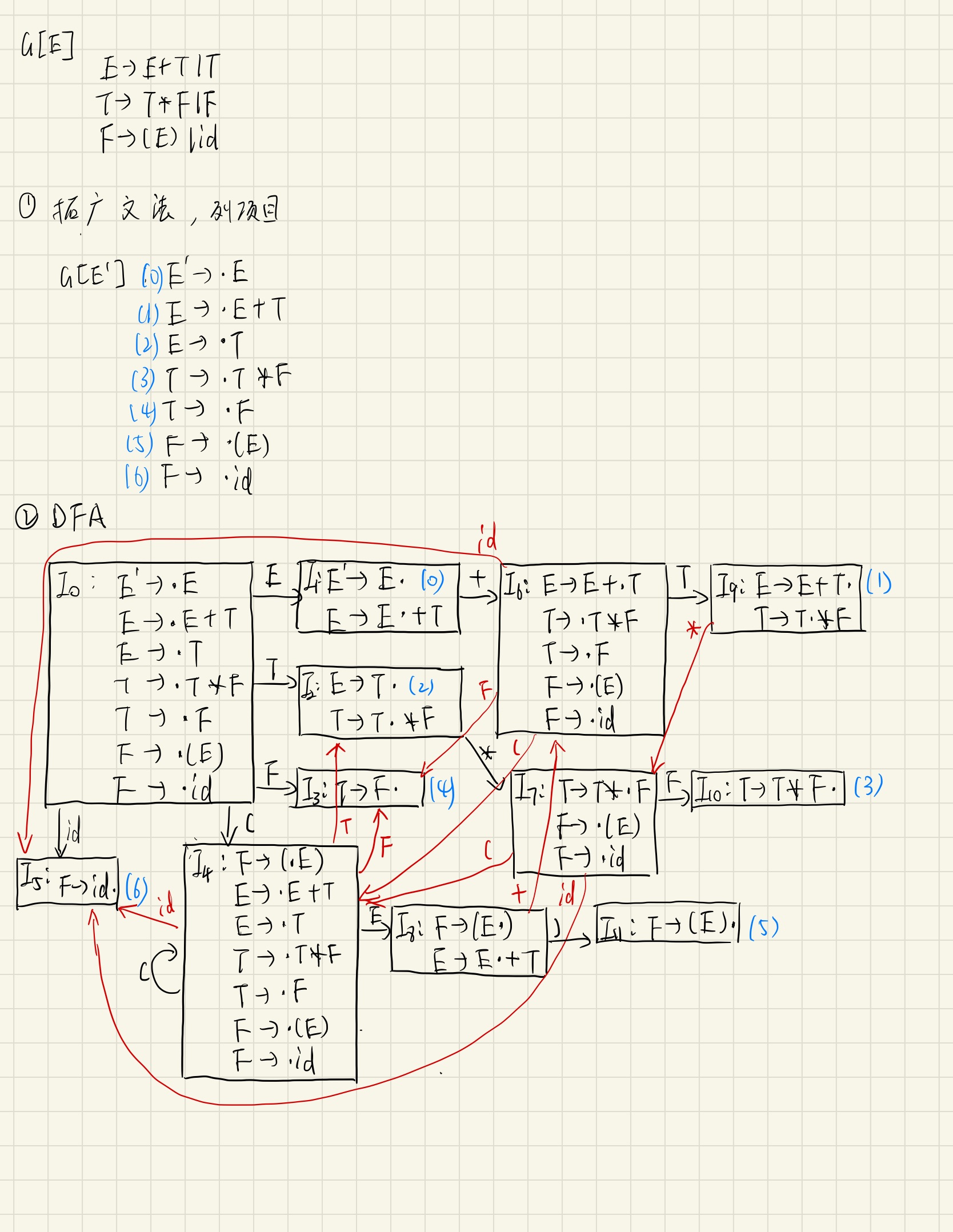
输入数据：

五、实验结果:

1、代码

#include <iostream>
#include <iomanip>
#include <stack>
#include <string>using namespace std;int table[20][20][2];// I,(non)terminals,action
int mp[200];//映射
string terminals = "+*()i$ETF";
string inputString = "(a+b)*c+(d+e)";
stack<int> pStk, iStk; //parse stack, input stack
stack<int> reduceResult;//存储规约结果, 用于分析树
string reduce[7][2]; //规约
int step = 1;namespace Graph { //处理分析树const int N = 1000, M = N * 2;int nodemap[N] = { 0, 'E' };int depth[N];struct Edge {int to, nxt;}e[M];int adt, head[N];void add(int u, int v) {e[++adt] = { v,head[u] };head[u] = adt;}int fa[N];void dfs(int p1) {//输出分析树for (int i = 0; i < depth[p1]; i++) {cout << "   |";}cout << "--" << (char)nodemap[p1] << endl;for (int i = head[p1]; i != 0; i = e[i].nxt) {int p2 = e[i].to;if (p2 == fa[p1]) continue;fa[p2] = p1;dfs(p2);}}void parseTree() {int vst[1000] = { 0 };depth[1] = 0;int cnt = 2;while (!reduceResult.empty()) {//读出规约结果int rTop = reduceResult.top(); reduceResult.pop();int leftChar = reduce[rTop][0][0];//产生式左部string rightString = reduce[rTop][1];//产生式右部int oldCnt = cnt;for (int j = oldCnt - 1; j >= 1; j--) {//从右往左匹配父节点if (nodemap[j] == leftChar and !vst[j]) {vst[j] = 1;for (char k : rightString) {nodemap[cnt] = k;//给节点编号 加映射depth[cnt] = depth[j] + 1;add(j, cnt);cnt++;}break;}}}dfs(1);}
}stack<int> reverse(stack<int> s) {stack<int> tmp;while (!s.empty()) {tmp.push(s.top());s.pop();}s = tmp;return s;
}string reverse(string s) {//禁止使用引用reverse(s.begin(), s.end());return s;
}void show(stack<int> ps, stack<int> is) {ps = reverse(ps);int width = 25;string str1, str2;int odd = 1;while (!ps.empty()) {if (odd == 1)  str1 += (char)ps.top();else str1 += to_string(ps.top());odd *= -1;ps.pop();}while (!is.empty()) {str2 += (char)is.top();is.pop();}string strBlank(width - str1.size() - str2.size(), ' ');cout << str1 << strBlank << str2;
}void init() {for (int i = 0; i < terminals.size(); i++) {mp[terminals[i]] = i; // 映射 (non)terminals -> numberif (terminals[i] == 'i') {// id = {a ~ z}for (int j = 'a'; j <= 'z'; j++) {mp[j] = i;}}}for (int i = 0; i <= 11; i++) {for (int j = 0; j < terminals.size(); j++) {char c; cin >> c;table[i][j][0] = c;}}for (int i = 0; i <= 11; i++) {for (int j = 0; j < terminals.size(); j++) {int num; cin >> num;table[i][j][1] = num;}}for (int i = 0; i < 7; i++) {cin >> reduce[i][0] >> reduce[i][1];reduce[i][1] = reverse(reduce[i][1]);}
}int parseTable() {pStk.push('$');pStk.push(0);iStk.push('$');for (int i = inputString.size() - 1; i >= 0; i--) {iStk.push(inputString[i]);}cout << "---------------------------"<< "--------------------------" << endl;cout << "Step   Parsing Stack       Input    Action" << endl;while (!iStk.empty() and !pStk.empty()) {cout << step << "     ";if (step++ < 10) putchar(' ');show(pStk, iStk);int pTop = pStk.top(), iTop = iStk.top();int action[2] = { table[pTop][mp[iTop]][0],table[pTop][mp[iTop]][1] };if (action[0] == 'A') {// 接受cout << "    Accept" << endl;return 200;} else if (action[0] == 'S') {// 移进cout << "    Shift " << action[1] << endl;pStk.push(iTop);pStk.push(action[1]);iStk.pop();} else if (action[0] == 'R') {// 规约reduceResult.push(action[1]);cout << "    Reduce " << action[1]<< ": " + reduce[action[1]][0] + " -> "<< reverse(reduce[action[1]][1]) << endl;for (auto i : reduce[action[1]][1]) {while (!pStk.empty()) {int c = pStk.top();pStk.pop();if (c == i) break;if (i == 'i') {if ('a' <= c && c <= 'z') break;}}}int pTop1 = pStk.top();pStk.push(reduce[action[1]][0][0]);int pTop2 = pStk.top();pStk.push(table[pTop1][mp[pTop2]][1]);} else {return 500;}}return 500;
}void solve() {init();int res = parseTable();if (res == 200) {puts("\nParsing Success");} else {puts("\nParsing Failed");}puts("\nParsing Tree:");Graph::parseTree();
}int main() {FILE* fp;freopen_s(&fp, "input.txt", "r", stdin);solve();fclose(fp);
}

input.txt 放在程序同目录下

n n S n S n Y Y Y
S n n n n A n n n
R S n R n R n n n
R R n R n R n n n
n n S n S n Y Y Y
R R n R n R n n n
n n S n S n n Y Y
n n S n S n n n Y
S n n S n n n n n
R S n R n R n n n
R R n R n R n n n
R R n R n R n n n0 0 4 0 5 0 1 2 36 0 0 0 0 0 0 0 02 7 0 2 0 2 0 0 04 4 0 4 0 4 0 0 00 0 4 0 5 0 8 2 36 6 0 6 0 6 0 0 00 0 4 0 5 0 0 9 30 0 4 0 5 0 0 0 10
6 0 0 11 0 0 0 0 01 7 0 1 0 1 0 0 03 3 0 3 0 3 0 0 05 5 0 5 0 5 0 0 0E' E
E E+T
E T
T T*F
T F
F (E)
F i

2、截图

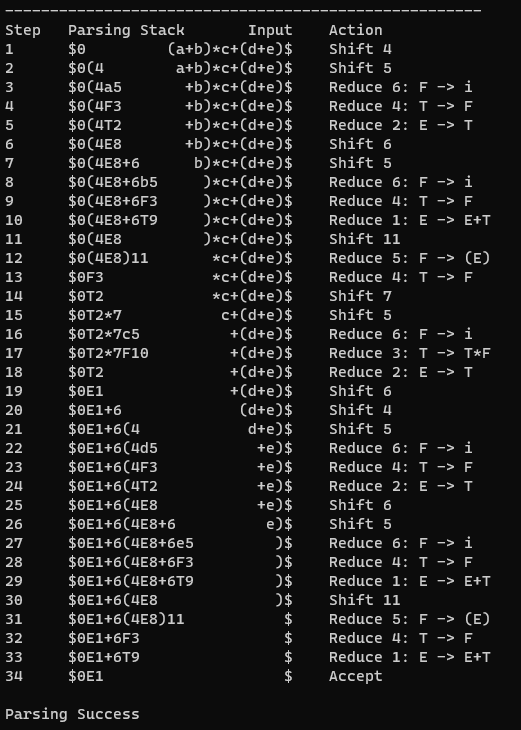
六、实验结论:

1 、实验结论

（是否能够准确描述实验的结论）

本实验使用SLR(1)文法，根据给定上下文无关文法，完成它的分析程序，并在结果中给出分析过程。

程序可以处理给定token序列不满足给定文法的情况。

此程序的优势是可以快速地修改以适用于不同的SLR(1)文法。

2、分析和总结

1）对输入设计的结论

Augmented Grammar使用string reduce[7][2];存储用于规约。

Parse Table使用int table[20][20][2];存储。分两次读入。

Terminals、Non-terminals直接硬编码到代码中。

2）对输出设计的结论

注意输出格式、栈的展示方向、数据左右对齐。

输出分析树时，先根据规约结果生成分析树存到邻接表中，然后DFS遍历整张图并输出。

3）对SLR(1)或者LR(1)分析法的结论

LR(0):见到First集就移进，见到终态就归约

SLR(1)见到First集就移进，见到终态先看Follow集，与Follow集对应的项目归约，其它报错。

SLR分析法包含的展望信息是体现在利用了Follow(A)信息，可以解决“归约－归约”冲突

SLR分析法没有包含足够的展望信息，不能完成解决“移进－归约”冲突，需要改进。

LALR同心集合并不会产生“移进－归约”冲突，但会产生“归约－归约”冲突

3、对预估问题的结论

程序需要事先获得Augmented Grammar、Parse Table、Terminals、Non-terminals的具体内容，这些数据都要被处理为适当的格式，过程比较繁琐。

Augmented Grammar使用string reduce[7][2];存储用于规约。

Parse Table使用int table[20][20][2];存储。分两次读入。

Terminals、Non-terminals直接硬编码到代码中。

可以将每个(non)terminal映射为数字，便于直接调用table(i,(non)terminal)。
注意非终结符id的特殊处理。

以下代码解决2、3问题

  for (int i = 0; i < terminals.size(); i++) {mp[terminals[i]] = i; // 映射 (non)terminals -> numberif (terminals[i] == 'i') {// id = {a ~ z}for (int j = 'a'; j <= 'z'; j++) {mp[j] = i;}}
}

在问题3处，还需注意规约时的字符替换处理。