✍个人博客：https://blog.csdn.net/Newin2020?spm=1011.2415.3001.5343
📣专栏定位：为 0 基础刚入门数据结构与算法的小伙伴提供详细的讲解，也欢迎大佬们一起交流~
📚专栏地址：https://blog.csdn.net/Newin2020/article/details/126445229
❤️如果有收获的话，欢迎点赞👍收藏📁，您的支持就是我创作的最大动力💪
🎏唠叨唠叨：在这个专栏里我将会整理 PAT 甲级的真题题解，并将他们进行分类，方便大家参考。

二分法

这一讲我们来介绍一个经常出现在我们视野中的算法 —— 二分法，想必大家都不陌生，利用它可以优化很多过程，使时间复杂度骤降，正如其名二分一样，不用从头往后一个个的遍历。

虽然作为基础算法之一，但是想要完全掌握它并不容易，最让人折磨的是它那“迷人”的边界问题。作为初学者，没必要研究的过于细致，会对自信心有很大的打击，可以先记下模板，后面题目做多了就会慢慢体会出来，接下来我将给大家讲解二分法的一些常用算法和模板。

在此之前需强调一下，二分法只适用于有序序列中，在无序序列中使用二分法没有任何意义。

整数二分

还是继承我们的传统，边讲题目边介绍算法，首先来看第一道开胃菜。

猜数问题

给定 100 以内的一个数，让我们猜出是哪个数。

如果从 1 遍历到 100 那显得比较麻烦，特别是当数字范围扩大时，比如扩大到 10 万，那时间复杂度将非常的高。

所以就要用到二分法来做，每次取中值进行判断，然后再不断地缩小范围，直到超出边界为止，它可以将时间复杂度从 O(1) 降到 O(log₂n)，还是很可观的。

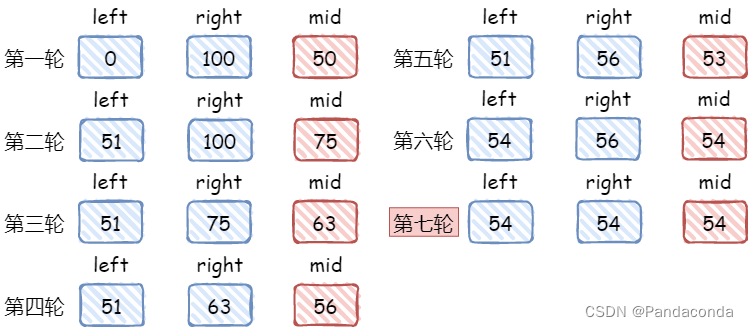
我们直接上代码：

#include<bits/stdc++.h>
using namespace std;
int a[1000];
int bin_search(int* a, int n, int x) {   //在数组a中找数字x，返回位置int left = 0, right = n;while (left < right) {int mid = left + (right - left) / 2;if (a[mid] >= x) right = mid;else             left = mid + 1;cout << a[mid] << " ";              //打印猜数的过程}return left;
}
int main() {int n = 100;for (int i = 0; i < n; i++) a[i] = i + 1;      //赋值，数字1~100int test = 54;                      //猜54这个数int pos = bin_search(a, n, test);cout << "\n" << "test=" << a[pos];
}

其中 mid=left+(right-left)/2 需要大家牢记，它等价于 mid=(left+right)/2，但因为防止整数过大导致溢出，所以我们常用前面那种写法。

另外，我相信这代码中最让人难以理解的是 left 和 right 两指针的边界问题，我这里采用的这种做法的 while 条件为 left<right 而不是 left<=right。这就考虑到循环内部的代码了，先来看看循环内部重点代码的含义分别是什么：

• int mid=left+(right-left)/2 表示取左边界 left 和右边界 right 的中值，但需要注意的是由于特性，编译器在计算时遇到小数会自动向下取整，比如 5/2=2，这是一个很关键的点。
• if(a[mid]>=x) right=mid 表示当中值大于等于目标值时，将右边界 right 缩小到 mid。因为目标值可能就是 mid，所以不能使 right=mid-1。
• else left=mid+1 表示当中值小于目标值时，将左边界 left 缩小到 mid+1。因为目标值现在只可能出现中值的右边，故如果使 left=mid 将毫无意义，已经确定 a[mid] 不是目标值了，并且还可能导致死循环。例如，left=0,right=1，则 mid=1/2=0，且 a[mid]<x，如果还让 left=mid 则循环将永远进行下去。

现在我们考虑，为什么不能让中值大于目标值时 right=mid-1 且中值小于等于目标值时 left=mid，即让上面判断条件反过来。还是上面那个例子，left=0,right=1，则 mid=1/2=0，且 a[mid]<=x，如果让 left=mid 则会死循环。当然也有解决方法，但为了避免混淆，只记住一种方法即可，在后续的使用中只用自己背过的那种处理方法。

但是这道题只是其中一种题型，我们需要背的不只这一个模板，因为这里解决的是一个确定的数，如果该数不存在怎么办，还需要进一步讨论，这就需要继续看我们下面的模板题了。

在单调递增序列中找 x 或者 x 的后继

在单调递增数列 a 中查找某个数 x，如果数列中没有 x，找比它大的第一个数。

这道题和上道题唯一不同的地方就是该题查找的数可能不存在，如果不存在则要找到大于它的第一个数，还是先来看代码：

#include<bits/stdc++.h>
using namespace std;
int a[1000];
int bin_search(int* a, int n, int x) {     //a[0]～a[n-1]是单调递增的int left = 0, right = n;              //注意：不是 n-1，此时是左闭右开的[0,n)while (left < right) {int mid = left + (right - left) / 2;  //int mid = (left + right) >> 1;if (a[mid] >= x)  right = mid;else    left = mid + 1;}                                     //终止于left = rightreturn left;
}
int main() {int n = 100;for (int i = 0; i < n; i++) a[i] = 2 * i + 2;      //赋值，数字2~200，偶数int test = 55;                        //找55或55的后继int pos = bin_search(a, n, test);cout << "test=" << a[pos];
}

可以发现，这个代码和上面一题的核心代码部分一模一样，说明这一类的题都可以用到这个模板。可能会有小伙伴有疑问，如果将 if else 中的条件互换会怎样，答案在下一道题中。

在单调递增序列中找 x 或者 x 的前驱

在单调递增数列 a 中查找某个数 x，如果数列中没有 x，找比它小的第一个数。

这道题咋一看好像和上题差不多，但代码却有区别，上面提到如果将 if else 中条件互换会怎样，来看代码：

#include<bits/stdc++.h>
using namespace std;
int a[1000];
int bin_search2(int* a, int n, int x) {    //a[0]～a[n-1]是单调递增的int left = 0, right = n;while (left < right) {int mid = left + (right - left + 1) / 2;if (a[mid] <= x)  left = mid;else  right = mid - 1;}                                     //终止于left = rightreturn left;
}
int main() {int n = 100;for (int i = 0; i < n; i++) a[i] = 2 * i + 2;     //赋值，数字2~200,偶数int test = 55;                       //找55或55的前驱int pos = bin_search2(a, n, test);cout << "test=" << a[pos];
}

可以发现把条件互换后，还变了一个地方就是 mid，不再是 mid=(left+right)/2，而是 mid=(left+right+1)/2，防止溢出改为 mid=left+(right-left+1)/2。这还是因为向下取整的特性，为了满足本题要求需要对此进行改动。

同样，如果将上面的 right=mid-1 改为 right=mid 也会出现死循环。

我们再来看一道稍微综合一点的模板题，帮助大家进一步理解。

数的范围

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 n 和 q，表示数组长度和询问个数。

第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。

接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式

共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例：

6 3
1 2 2 3 3 4
3
4
5

输出样例：

3 4
5 5
-1 -1

这道题是不是看起来有点眼熟，好像和前面两题求前驱和后继的题目有点类似，还是先来看代码：

#include<bits/stdc++.h>
using namespace std;int k, n, q;
int arr[100010];//后继的代码模板 —— 找左端点
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;if (arr[mid] < k)   l = mid + 1;else r = mid;}return l;
}//前驱的代码模板 —— 找右端点
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;if (arr[mid] <= k) l = mid;else   r = mid - 1;}return l;
}int main()
{scanf("%d%d", &n, &q);for (int i = 0; i < n; i++){scanf("%d", &arr[i]);}while (q--){scanf("%d", &k);int x = bsearch_1(0, n - 1);	//寻找左端点if (arr[x] != k)    printf("-1 ");else printf("%d ", x);x = bsearch_2(0, n - 1);	//寻找右端点if (arr[x] != k)    printf("-1\n");else printf("%d\n", x);}return 0;
}

本题需要我们找到目标值的相同区间，其中用到的代码模板就是前面两题的模板，归类一下：

• 寻找左端点：套用后继代码模板
• 寻找右端点：套用前驱代码模板

这样一看是不是要明朗一些，很多题目其实就是基于这些模板扩展来的。

浮点数二分

浮点数二分就没有整数二分那种烦人的边界问题，因为没有了向下取整，我们只需要考虑其中的精度问题，还是先来看一道模板题。

数的三次方根

给定一个浮点数 n，求它的三次方根。

输入格式

共一行，包含一个浮点数 n。

输出格式

共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围

−10000≤n≤10000

输入样例：

1000.00

输出样例：

10.000000

这道题一开始看可能会有点懵，不知道这和二分有啥关系。在上面的模板当中，if 语句中的判断其实是可以变的，根据题目的要求进行变化。这道题我们可以对数的三次方根进行二分，先来看代码：

#include<bits/stdc++.h>
using namespace std;double n;int main()
{cin >> n;const double eps = 1e-8;double l = -100, r = 100;while (r - l > eps){double mid = (r + l) / 2;if (mid * mid * mid >= n)   r = mid;else l = mid;}printf("%.6lf\n", l);return 0;
}

可以发现我们将左边界和右边界分别设置为了 l=-100 和 r=100，这样能够包含数据的范围，计算时区间回往中间收缩直至找到答案。另外，不用再因为边界问题而苦恼，l 和 r 在收缩时不用加一减一，直接等于 mid 即可。

但是要注意的是，浮点数会存在精度问题，可能 r 和 l 永远不相等，所以我们需要模拟相等的情形即只要 r 和 l 的差值足够小，我们就认为它相等。题目要求保留 6 位小数，所以我们可以将精度设置为 1e-8，即当 r-l 只要小于等于 1e-8，我们就认为此时已经收敛到某个值，直接退出循环即可。

总结

恭喜您成功点亮二分算法技能点！

通过上面这么多道模板题，可以发现其中的一些规律，这些题目的二分模板其实都差不多，但是从浮点数二分的模板题来看好像模板中 if 条件可能不同。很多题目不会明摆的告诉你这道题可以用二分来做，需要我们自己去找到其中的划分依据作为 if 中的判断条件，不过大体上模板都是一样的，因此二分的应用场景为：

1. 存在一个有序的序列
2. 可以将题目建模在一个有序序列上查找一个合适的数值

另外，我们仍然可以得出大部分题目通用的模板，如下：

整数二分通用模板

bool check(int x) {/* ... */} //检查x是否满足某种性质//区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用，例如求一串相同数字的左边界或者某个数字及其后驱
//也就是说我们要找的这个点要尽可能的小，不断缩小右边界，但是每次的结果可能是目标值，故r=mid
int bsearch_1(int l, int r) {while (l < r) {int mid = l + (r - l) / 2;	//这样可以防止爆intif (check(mid))	//mid满足条件，需要保留r = mid;    //check()判断mid是否满足性质elsel = mid + 1;}return l;
}//区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用，例如求一串相同数字的右边界或者某个数字及其前驱
//也就是说我们要找的这个点要尽可能的大，不断缩小左边界，但是每次的结果可能是目标值，故l=mid
int bsearch_2(int l, int r) {while (l < r) {//这里要加1是因为除法是向下取整，如果不加1那么当只有两个数时，l=mid会进入死循环int mid = l + r + 1 >> 1;if (check(mid))	//mid满足条件，需要保留l = mid;elser = mid - 1;}return l;
}

浮点数二分通用模板

bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}