自动驾驶教程：From Pixels to Meters

Inverse perspective mapping

测到哪些像素坐标 $(u, v)$ 是车道边界的一部分之后，我们现在想要知道哪些3维点 $X_c,Y_c,Z_c)$ 对应于这些像素坐标。首先让我们再次看一下这个图像形成过程的草图：
在这里插入图片描述
请记住：给定相机参考系中的3维点 $X_c,Y_c,Z_c)$ ，我们可以通过以下方法获得像素坐标 $(u, v)$

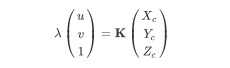
但是我们现在需要做的是解决逆问题。我们已经给出了 $(u, v)$ ，并且需要知道 $X_c,Y_c,Z_c)$ 。为此，我们将上面的方程式乘以：
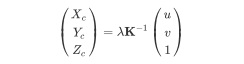
在这里插入图片描述
我们的问题是我们不知道 $λ$ 的值。这意味着对应于像素坐标的3d点 $X_c,Y_c,Z_c)$ 位于由定义的直线上的某处坐标 $(u, v)$

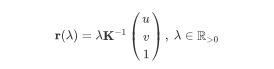
但是，哪个 $λ$ 产生了我们图像中捕获的点呢？通常，这个问题无法回答。但是在这里，我们可以利用我们应该掌握的知识 $r (λ)$ 对应于车道边界上的一个点。我们将假设道路是平坦的。平面可以通过法向矢量 $n$ 和位于该平面上的某些点 $r_0$ 来表征
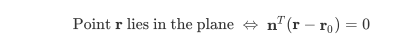
在这里插入图片描述

在道路参考系中，法线向量为 $n={(0,1,0)}^T$ 。由于相机的光轴不平行于道路，相机参考系中的法向矢量为 $n_c=R_{cr}{(0,1,0)}^T$ ,旋转矩阵 $R_{cr}$ 描述了摄像机相对于道路定向：它将矢量从道路框架旋转到摄像机框架。剩下的缺失部分是平面上的某个点 $r_0$ 。在相机参考系中，相机在位置 ${(0,0,0)}^T$ .如果我们用 $h$ 表示摄像机在道路上方的高度,那么我们可以通过沿道路法线向量 $n_c$ 的方向移动距离为h.因此，我们选取 $r_0=hn_c$ ,我们的平面方程变为
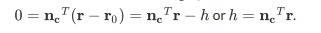
在这里插入图片描述

现在我们可以计算线 $r(\lambda)={\lambda K}^{-1} {(u,v,1)}^T$ 到达道路的点，通过把 $r(\lambda)$ 带入平面等式 $h={n_c}^Tr$

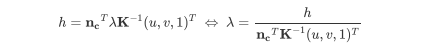
在这里插入图片描述
我们可以吧 $\lambda$ 的值代入 $r(\lambda)$ 来得到从像素坐标 $(u, v)$ 映射到相机参考系相应的三维坐标

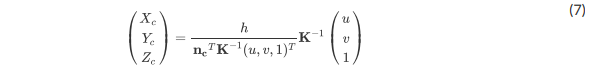
仅当图像以像素坐标 $(u, v)$ 显示道路时，此方程式才成立。它可能看起来有些丑陋，但实际上很容易用python实现。

Exercise: Inverse perspective mapping

在本练习中，您将实现等式。（7）以及摄像机参考系和道路参考系之间的坐标转换。对于后一部分，您可能会回顾“图像形成基础”。请注意，在进行本练习之前，您应该已经成功完成了《图像形成基础》中的练习。
要开始练习，请打开代码/tests/lane_detection/inverse_perspective_mapping.ipynb，然后按照该笔记本中的说明进行操作

Fitting the polynomial

我们的目标是获得多项式 $y_l(x)$ 和 $y_r(x)$ 并描述道路参考系中的左右车道边界（基于ISO 8855）。

在这里插入图片描述

import numpy as np
import matplotlib.pyplot as plt

从车道边界分割中，我们知道我们的语义分割模型将以摄像机图像作为输入，并返回形状为（H，W，3）的张量输出。特别是prob_left = output [v，u，1]将是像素是左车道边界的一部分的概率。我将神经网络为某些示例图像计算的张量输出[v，u，1]保存在一个npy文件中。我们来看一下

prob_left = np.load("../../data/prob_left.npy")
plt.imshow(prob_left, cmap="gray")
plt.xlabel("$u$");
plt.ylabel("$v$");

在这里插入图片描述
上图显示了每个（u，v）的prob_left [v，u]。现在想象一下，而不是三元组（u，v，prob_left [v，u]），我们将有三元组（x，y，prob_left（x，y）），如图18所示，这是道路上的坐标。这些三元组可以针对prob_left [x，y]大的所有（x，y，prob_left [x，y]）过滤掉。我们将获得属于左车道边界的点的列表，并可以使用这些点来设置多项式！但是，从（u，v，prob_left [v，u]）转到（x，y，prob_left [x，y]）实际上并不难，因为在上一练习中实现了uv_to_roadXYZ_roadframe_iso8855函数。此函数转换为（请注意，对于道路像素）

import sys
sys.path.append('../../code')
from solutions.lane_detection.camera_geometry import CameraGeometry
cg = CameraGeometry()
xyp = []
for v in range(cg.image_height):
for u in range(cg.image_width):
X,Y,Z= cg.uv_to_roadXYZ_roadframe_iso8855(u,v)
xyp.append(np.array([X,Y,prob_left[v,u]]))
xyp = np.array(xyp)

这个double for循环非常慢，但是请放心。 xyp数组的前两列与prob_left无关，因此可以进行预先计算。可以不使用for循环来计算最后一列：xyp [：，2] == prob_left.flatten（）。您将在练习中进行预计算。
为了将自己限制为具有较大prob_left [x，y]的三元组（x，y，prob_left [x，y]），我们可以创建一个蒙版。然后，我们可以将屏蔽的x和y值插入numpy.polyfit（）函数，以最终获得所需的多项式。 numpy.polyfit（）执行最小二乘。但是，如果我们传递一系列权重，它甚至可以进行最小二乘加权。我们只将概率值作为权重传递，因为高概率的（x，y）点应该被加权

x_arr, y_arr, p_arr = xyp[:,0], xyp[:,1], xyp[:,2]
mask = p_arr > 0.3
coeffs = np.polyfit(x_arr[mask], y_arr[mask], deg=3, w=p_arr[mask])
polynomial = np.poly1d(coeffs)

Let’s plot our polynomial:

x = np.arange(0,60,0.1)
y = polynomial(x)
plt.plot(x,y)
plt.xlabel("x (m)"); plt.ylabel("y (m)"); plt.axis("equal");

在这里插入图片描述

Encapsulate the pipeline into a class

现在，您已经看到了车道检测管道的两个步骤：车道边界分割和多项式拟合。为了将来使用，将整个管道封装到一个类中很方便。在下面的练习中，您将实现这样的LaneDetector类。现在，让我们看一下实际应用中的LaneDetector的示例解决方案。首先，我们加载一张图片

import cv2
img_fn = "images/carla_scene.png"
img = cv2.imread(img_fn)
img = cv2.cvtColor(img, cv2.COLOR_BGR2RGB)
plt.imshow(img);

在这里插入图片描述
现在，我们导入LaneDetector类并创建一个实例。为此，我们指定了使用pytorch的save函数存储的模型的路径

from solutions.lane_detection.lane_detector import LaneDetector
model_path ="../../code/solutions/lane_detection/best_model_multi_dice_loss.pth"
ld = LaneDetector(model_path=model_path)

从现在开始，我们可以将任何图像传递给ld实例，以获取任何图像的车道边界多项式（与训练集的差别不大）。
poly_left, poly_right = ld(img)
在Google Colab上，此调用大约需要45毫秒。对于实时应用程序来说，这还不够好，在实时应用程序中，您期望的时间为10-30毫秒或更短，但是已经接近了。该样本解决方案的瓶颈是神经网络。也许您实施了一个更有效的方法？如果要使系统更快，还可以考虑在训练和推理期间将较低分辨率的图像馈入网络。这将牺牲准确性与速度。如果您尝试一下，请让我知道它的效果如何;）

现在让我们看一下ld计算出的多项式

x = np.linspace(0,60)
yl = poly_left(x)
yr = poly_right(x)
plt.plot(x, yl, label="yl")
plt.plot(x, yr, label="yr")
plt.xlabel("x (m)"); plt.ylabel("y (m)");
plt.legend(); plt.axis("equal");