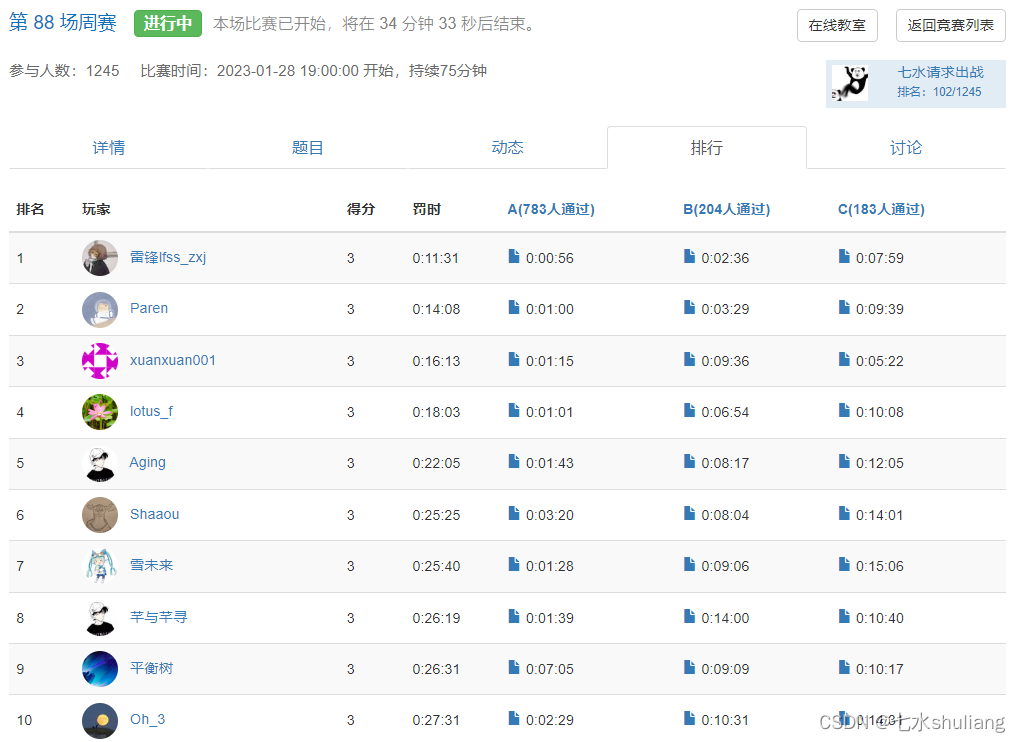
一、本周周赛总结

• 在T2卡了半天，因为自己封的RS读入字符串方法要加个逗号，于是先去做了T3再回来做T2。
• T1 暴力
• T2 Floyd
• T3 线性DP

二、 4800. 下一个

链接: 4800. 下一个

1. 题目描述

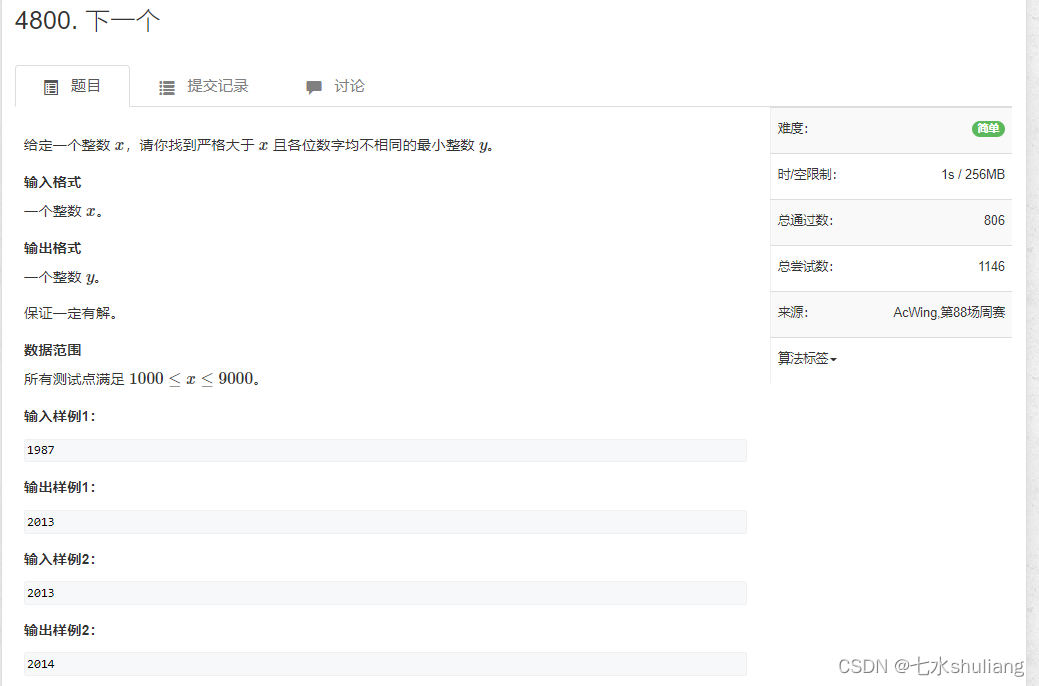
2. 思路分析

签到题，暴力找。

3. 代码实现

# Problem: 下一个
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4803/
# Memory Limit: 256 MB
# Time Limit: 1000 msimport sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from math import sqrt, gcd, inf
# ACW没有comb
# from math import sqrt, gcd, inf, comb
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')#       ms
def solve():n, = RI()n += 1while True:s = str(n)if len(s) == len(set(s)):return print(n)n += 1if __name__ == '__main__':solve()

三、4801. 强连通图

链接: 4801. 强连通图

1. 题目描述

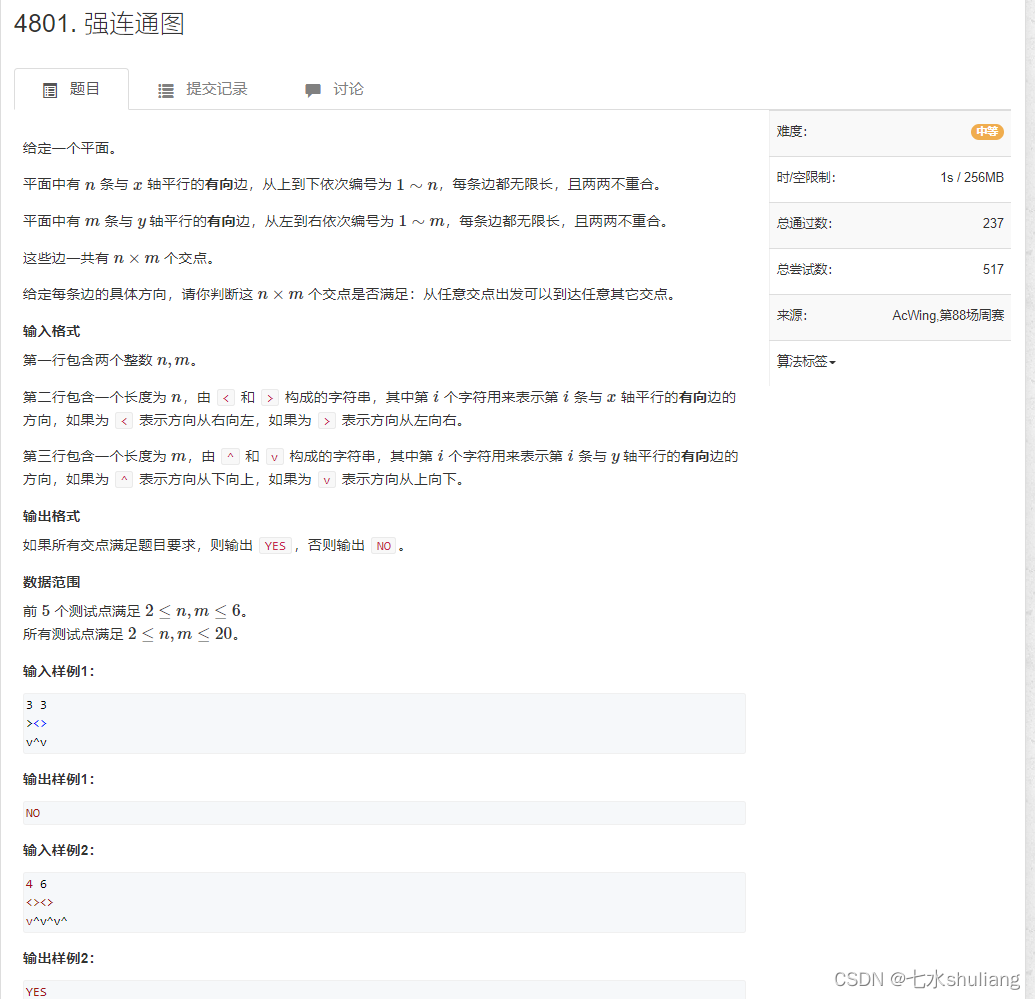
2. 思路分析

• 求所有点到所有点都能连通/最短距离，第一时间先想floyd。
• 看了下数据范围，n<=m<=20,最多400个点，n立方是可行的。因此给点编号，直接上floyd。
• 一共z = n*m个点，二维数组dis[u][v] 代表点u到点v是否连通。
• 然后枚举每个点作为跳板k，看看从u到k和从k到v是否连通，则连通uv。

---

• 赛后发现，只要四周能互相到达，就等于全图能连通。
• 因此只判断外围即可，即外围只有两种方案的字符串，顺时针或逆时针，直接判断即可。

3. 代码实现

# Problem: 强连通图
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4804/
# Memory Limit: 256 MB
# Time Limit: 1000 msimport sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from math import sqrt, gcd, inf
# ACW没有comb
# from math import sqrt, gcd, inf, comb
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')MOD = 10 ** 9 + 7#       ms
def solve():n, m = RI()a, = RS()b, = RS()# print(a,b)z = m * ndis = [[False] * z for _ in range(z)]for i in range(z):dis[i][i] = Truefor i, c in enumerate(a):if c == '>':for j in range(m - 1):u = i * m + jv = i * m + j + 1dis[u][v] = Trueelse:for j in range(m - 1):v = i * m + ju = i * m + j + 1dis[u][v] = Truefor j, c in enumerate(b):if c == 'v':for i in range(n - 1):u = i * m + jv = (i+1) * m + jdis[u][v] = Trueelse:for i in range(n - 1):v = i * m + ju = (i+1) * m + jdis[u][v] = Truefor k in range(z):for i in range(z):for j in range(z):if dis[i][k] and dis[k][j]:dis[i][j] = True# print(dis)for i in range(z):for j in range(z):if not dis[i][j]:return print('NO')print('YES')if __name__ == '__main__':solve()

四、4802. 金明的假期

链接: 4802. 金明的假期

1. 题目描述

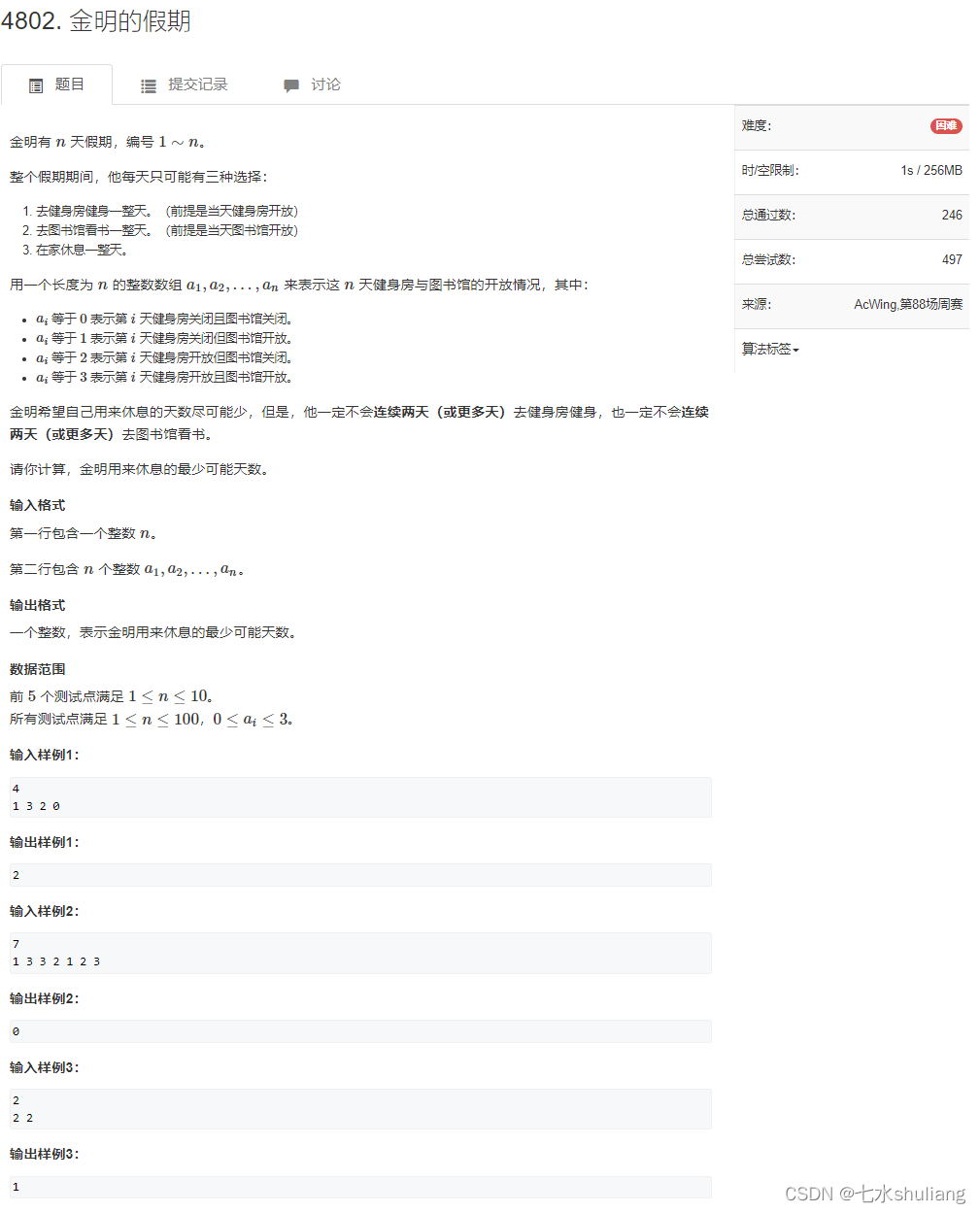
2. 思路分析

蛮裸的线性DP。

• 定义:令f[i][0/1/2]代表第i天， 小明选择休息/看书/健身时，最少休息次数。

• 转移:显然，只有对应的房间开放，才能选择今天进行这个活动，并且从昨天其他房间转移。

  • 问题变成如何判断对应房间开放，硬if有点麻烦，这里用位运算。
  • a[i] & 1 == 1 代表图书馆开，可以看书。
    • f[i][1] = min(f[i - 1][0], f[i - 1][2])
  • a[i] & 2 == 2 代表健身房开，可以健身
    • f[i][2] = min(f[i - 1][0], f[i - 1][1])
  • 任意时间可以休息，f[i][0] = min(f[i-1])

• 初始:显然第一天休息的话f[0] = 1；在第一天对应房间开方情况下，对应位置都是0.其他设置为inf。

• 答案:min(f[-1])。注意f[-1][0]也可能是答案，因为最后一天可能什么都不开，只能休息。

• 实现时可以滚动优化。（但这题没有空间问题，考试时没必要）

3. 代码实现

# Problem: 金明的假期
# Contest: AcWing
# URL: https://www.acwing.com/problem/content/4805/
# Memory Limit: 256 MB
# Time Limit: 1000 msimport sys
import bisect
import random
import io, os
from bisect import *
from collections import *
from contextlib import redirect_stdout
from itertools import *
from math import sqrt, gcd, inf
# ACW没有comb
# from math import sqrt, gcd, inf, comb
from array import *
from functools import lru_cache
from types import GeneratorType
from heapq import *RI = lambda: map(int, sys.stdin.buffer.readline().split())
RS = lambda: map(bytes.decode, sys.stdin.buffer.readline().strip().split())
RILST = lambda: list(RI())
DEBUG = lambda *x: sys.stderr.write(f'{str(x)}\n')MOD = 10 ** 9 + 7#    4330   ms
def solve1():n, = RI()a = RILST()f = [[inf] * 3 for _ in range(n)]  # 0/1/2 休息  看书 健身f[0][0] = 1if a[0] & 1:f[0][1] = 0if a[0] & 2:f[0][2] = 0for i in range(1, n):v = a[i]f[i][0] = min(f[i - 1]) + 1if v & 1:f[i][1] = min(f[i - 1][0], f[i - 1][2])if v & 2:f[i][2] = min(f[i - 1][0], f[i - 1][1])print(min(f[-1]))#   4274     ms
def solve():n, = RI()a = RILST()y = z = inf  # 休息  看书 健身x = 0for v in a:x, y, z = min(x, y, z) + 1, min(x, z) if v & 1 else inf, min(x, y) if v & 2 else infprint(min(x, y, z))if __name__ == '__main__':solve()

六、参考链接

• 无