四旋翼无人机
- 四旋翼无人机的动力学模型
- 四旋翼无人机的姿态表示
- Z-Y-X 欧拉角
- 欧拉角微分方程
- 四元数
- 四元数与虚数
- 四元数乘法
- 四元数微分方程
- 四旋翼无人机的姿态解算
- 传感器的特性
- 加速度补偿陀螺仪
- 磁力计补偿陀螺仪
- 四旋翼无人机的控制
- PID控制
四旋翼无人机的动力学模型
为了建立起能够描述无人机的物理和运动特性的方程，需要定义建模时的坐标系。定义两种坐标系：固定坐标系（惯性坐标系）{A}和无人机的机身坐标系{B}。使用欧拉角 ξ = ( ϕ , θ , ψ ) T \xi {\rm{ = }}{\left( {\phi, \theta ,\psi } \right)^T} ξ=(ϕ,θ,ψ)T表示在机身坐标系中无人机绕各个轴转动的角度， P = ( x , y , z ) T P={\left( {x, y ,z } \right)^T} P=(x,y,z)T表示无人机重心坐标。无人机为"X"型，无人机质量为 m m m，机臂长度为 l l l，绕无人机三个轴转动的转动惯量分别为 I x x , I y y , I z z I_{xx},I_{yy},I_{zz} Ixx,Iyy,Izz。无人机结构图如下
四个旋翼的升力分别为 F 1 , F 2 , F 3 , F 4 F_1,F_2,F_3,F_4 F1,F2,F3,F4，都沿着无人机机身 z z z轴方向。总升力 u 1 = F 1 + F 2 + F 3 + F 4 u_1=F_1 + F_2 + F_3 + F_4 u1=F1+F2+F3+F4, 作用于 x x x轴的力矩 u 2 = l 2 ( − F 1 − F 2 + F 3 + F 4 ) u_2=\dfrac{l}{{\sqrt 2 }}( - F_1 - F_2 + F_3 + F_4) u2=2l(−F1−F2+F3+F4), 作用于 y y y轴的力矩 u 3 = l 2 ( − F 1 + F 2 + F 3 − F 4 ) u_3=\dfrac{l}{{\sqrt 2 }}( - F_1 +F_2 + F_3 - F_4) u3=2l(−F1+F2+F3−F4), 作用于 z z z轴的力矩（扭矩） u 4 = − b ( F 1 + F 2 − F 3 + F 4 ) u_4= -b( F_1 + F_2 - F_3 + F_4) u4=−b(F1+F2−F3+F4), 其中 b b b 是力到扭矩的系数。根据牛顿-欧拉方程可得无人机运动学方程
I Ω ˙ + Ω × I Ω = N I\dot \Omega + \Omega \times I\Omega = N IΩ˙+Ω×IΩ=N其中I是无人机惯性张量矩阵，认为无人机机身对称，则 I = d i a g ( I x x , I y y , I z z ) I = diag(I_{xx},I_{yy},I_{zz}) I=diag(Ixx,Iyy,Izz)， Ω \Omega Ω表示无人机绕各个轴转动的角速度 Ω = ( ϕ ˙ , θ ˙ , ψ ˙ ) T \Omega=({\dot \phi, \dot \theta ,\dot \psi } )^T Ω=(ϕ˙,θ˙,ψ˙)T， N N N表示作用在无人机上的合力矩， N = ( u 2 ， u 3 ， u 4 ) T N=(u_2，u_3，u_4)^T N=(u2，u3，u4)T。展开得
ϕ ¨ = θ ˙ ψ ˙ I y y − I z z I x x + u 2 I x x \ddot \phi = \dot \theta \dot \psi \dfrac{{{I_{yy}} - {I_{zz}}}}{{{I_{xx}}}} + \dfrac{u_2}{{{I_{xx}}}} ϕ¨=θ˙ψ˙IxxIyy−Izz+Ixxu2 θ ¨ = ϕ ˙ ψ ˙ I z z − I x x I y y + u 3 I y y \ddot \theta = \dot \phi \dot \psi \dfrac{{{I_{zz}} - {I_{xx}}}}{{{I_{yy}}}} + \dfrac{u_3}{{{I_{yy}}}} θ¨=ϕ˙ψ˙IyyIzz−Ixx+Iyyu3 ψ ¨ = θ ˙ ϕ ˙ I x x − I y y I z z + u 4 I z z \ddot \psi = \dot \theta \dot \phi \dfrac{{{I_{xx}} - {I_{yy}}}}{{{I_{zz}}}} + \dfrac{u_4}{{{I_{zz}}}} ψ¨=θ˙ϕ˙IzzIxx−Iyy+Izzu4由牛二定律
m a = B A R z y x F ma=_B^A{R_{zyx}} F ma=BARzyxF其中 a = ( x ¨ ， y ¨ ， z ¨ ) T a=(\ddot x，\ddot y，\ddot z)^T a=(x¨，y¨，z¨)T， F = ( 0 ， 0 ， u 1 ) T F=(0，0，u_1)^T F=(0，0，u1)T。 B A R z y x _B^A{R_{zyx}} BARzyx的计算在后面。展开得
x ¨ = u 1 ( cos ϕ sin θ cos ψ + sin ϕ sin ψ ) m \ddot x = \dfrac{{u_1(\cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi )}}{m} x¨=mu1(cosϕsinθcosψ+sinϕsinψ) y ¨ = u 1 ( cos ϕ sin θ sin ψ − sin ϕ cos ψ ) m \ddot y = \dfrac{{u_1(\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi )}}{m} y¨=mu1(cosϕsinθsinψ−sinϕcosψ) z ¨ = u 1 cos ϕ cos θ m − g \ddot z = \dfrac{{u_1\cos \phi \cos \theta }}{m} - g z¨=mu1cosϕcosθ−g
四旋翼无人机的姿态表示
Z-Y-X 欧拉角
先将{B}坐标系绕{B}的z轴旋转 ψ \psi ψ角得到{C}坐标系，再将{C}坐标系绕{C}的y轴旋转 θ \theta θ角得到{D}坐标系，再将{D}坐标系绕{D}的x轴旋转 ϕ \phi ϕ角得到{A}坐标系，那么{B}坐标系变换到{A}坐标系的旋转矩阵为 B A R z y x = B C R z ⋅ C D R y ⋅ D A R x _B^A{R_{zyx}} = _B^C{R_z} \cdot _C^D{R_y} \cdot _D^A{R_x} BARzyx=BCRz⋅CDRy⋅DARx
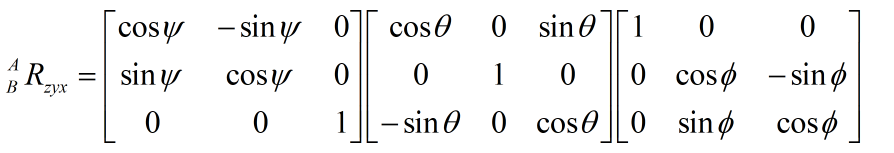
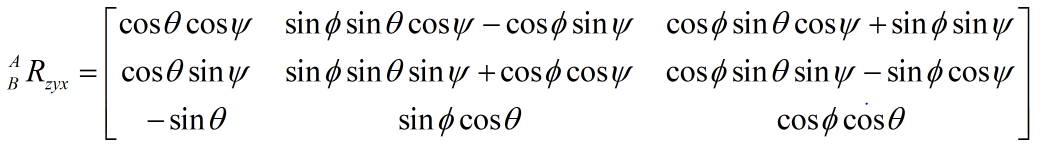
容易得到 ( B A R z y x ) − 1 = A B R z y x = ( B A R z y x ) T {\left( {_B^A{R_{zyx}}} \right)^{ - 1}} = _A^B{R_{zyx}} = {\left( {_B^A{R_{zyx}}} \right)^T} (BARzyx)−1=ABRzyx=(BARzyx)T{B}坐标系中向量 B p = ( x 0 , y 0 , z 0 ) ^Bp= \left({{x_0},{y_0},{z_0}} \right) Bp=(x0,y0,z0)在{A}坐标系中表示为· A p = ( x 1 , y 1 , z 1 ) ^Ap= \left({{x_1},{y_1},{z_1}} \right) Ap=(x1,y1,z1)，那么
A p = B A R z y x B p ^Ap=_B^A{R_{zyx}} ^Bp Ap=BARzyxBp
欧拉角微分方程
对上面的 B A R z y x _B^A{R_{zyx}} BARzyx求微分，得
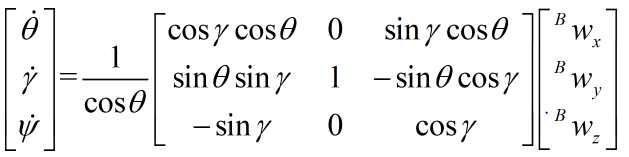
具体过程参见yangoming的博客(http://blog.sina.com.cn/s/blog_40edfdc90102wazm.html)
当 θ = π / 2 \theta=\pi/2 θ=π/2时会遇到万向节死锁，转动失去一个自由度，欧拉角微分方程无法表示，所以四元数微分方程而不用欧拉角微分方程。
四元数
四元数与虚数
我们都知道虚数形式为 q = w + x ⋅ i ⃗ q = w + x \cdot\vec i q=w+x⋅i可以写为 q = w + x ⋅ i ⃗ + 0 ⋅ j ⃗ + 0 ⋅ k ⃗ q = w + x \cdot \vec i + 0\cdot\vec j + 0\cdot\vec k q=w+x⋅i+0⋅j+0⋅k 单位虚数 q ^ = e i θ = cos θ + i ⃗ ⋅ s i n θ = cos θ + sin θ ( 1 ∗ i ⃗ + 0 ∗ j ⃗ + 0 ∗ k ⃗ ) \hat q= {e^{i\theta }}=\cos \theta + \vec i\cdot sin \theta=\cos \theta + \sin \theta \left( {1*\vec i + 0*\vec j + 0*\vec k} \right) q^=eiθ=cosθ+i⋅sinθ=cosθ+sinθ(1∗i+0∗j+0∗k) p ^ q \hat pq p^q可以表示一个向量 p p p绕轴（或向量） ( 1 , 0 , 0 ) (1,0,0) (1,0,0)旋转 θ \theta θ得到的向量。
四元数是虚数的扩展，一个四元数可以表示为 q = w + x i ⃗ + y j ⃗ + z k ⃗ q = w + x\vec i + y\vec j + z\vec k q=w+xi+yj+zk 单位四元数 q ^ = e θ 2 ( x i ⃗ + y j ⃗ + z k ⃗ ) = cos θ 2 + ( x i ⃗ + y j ⃗ + z k ⃗ ) sin θ 2 {\hat q=e^{\frac{\theta }{2}\left( {x\vec i + y\vec j + z\vec k} \right)}} = \cos {\frac{\theta }{2}} + \left( {x\vec i + y\vec j + z\vec k} \right)\sin {\frac{\theta }{2}} q^=e2θ(xi+yj+zk)=cos2θ+(xi+yj+zk)sin2θ且 q ^ p q ^ ∗ \hat qp{{\hat q}^ * } q^pq^∗可以表示一个向量 p p p绕轴（或向量） ( x , y , z ) ( x,y,z) (x,y,z)旋转 θ \theta θ得到的向量。其中 x 2 + y 2 + z 2 = 1 {x^2} + {y^2} + {z^2} = 1 x2+y2+z2=1， q ^ ∗ {{\hat q}^ * } q^∗是 q ^ \hat q q^的共轭。
四元数乘法
简便起见四元数可以写为 q = w + v ⃗ ⋅ x ⃗ = ( w , v ⃗ ) q = w + \vec v \cdot \vec x=(w,\vec v) q=w+v⋅x=(w,v)其中 w w w为标量， v v v为向量 , v ⃗ = ( x , y , z ) , x ⃗ = ( i ⃗ , j ⃗ , k ⃗ ) ,\vec v = \left( {x,y,z} \right),\vec x = \left( {\vec i,\vec j,\vec k} \right) ,v=(x,y,z),x=(i,j,k)
两个四元数的乘法按多项式乘法进行, i ⃗ j ⃗ = k ⃗ , j ⃗ k ⃗ = i ⃗ , k ⃗ i ⃗ = j ⃗ \vec i\vec j = \vec k,\vec j\vec k = \vec i,\vec k\vec i{\rm{ = }}\vec j ij=k,jk=i,ki=j q 1 = ( w 1 , v ⃗ 1 ) {q_1} = \left( {{w_1},{\vec v_1}} \right) q1=(w1,v1), q 2 = ( w 2 , v ⃗ 2 ) {q_2} = \left( {{w_2},{\vec v_2}} \right) q2=(w2,v2)， q 1 q 2 {q_1q_2} q1q2化简得 w 1 w 2 − v ⃗ 1 ⋅ v ⃗ 1 , v ⃗ 1 × v ⃗ 2 + w 1 v ⃗ 2 + w 2 v ⃗ 1 {{w_1w_2-\vec v_1 \cdot \vec v_1},{\vec v_1 \times \vec v_2+w_1\vec v_2+w_2\vec v_1}} w1w2−v1⋅v1,v1×v2+w1v2+w2v1假设单位四元数 q ^ = q 0 + q 1 i ⃗ + q 2 j ⃗ + q 3 k ⃗ \hat q = q_0+ q_1\vec i + q_2\vec j + q_3\vec k q^=q0+q1i+q2j+q3k可以表示为 q ^ = [ q 0 , q 1 , q 2 , q 3 ] \hat q = \left[ {q_0},{q_1},{q_2},{q_3}\right] q^=[q0,q1,q2,q3] 向量 p = ( x 0 , y 0 , z 0 ) p= \left({{x_0},{y_0},{z_0}} \right) p=(x0,y0,z0)的四元数 p = [ 0 , x 0 , y 0 , z 0 ] p= \left[ 0,{{x_0},{y_0},{z_0}} \right] p=[0,x0,y0,z0]。
p ′ = q ^ p q ^ ∗ p' =\hat qp{{\hat q}^ * } p′=q^pq^∗得到四元数 p ′ = [ 0 , x 1 , y 1 , z 1 ] p'= \left[ 0,{{x_1},{y_1},{z_1}} \right] p′=[0,x1,y1,z1]。对应的向量 p ′ = ( x 1 , y 1 , z 1 ) p' = \left( {{x_1},{y_1},{z_1}} \right) p′=(x1,y1,z1)。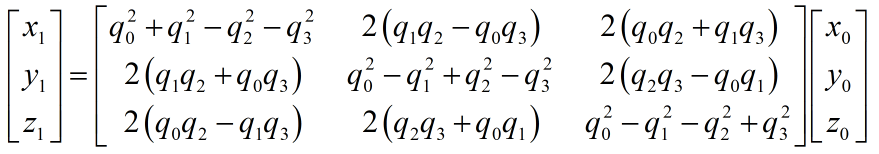
对比欧拉角旋转矩阵，可以知道
四元数微分方程
假设单位四元数 q = cos θ 2 + n ⃗ sin θ 2 q = \cos \frac{\theta }{2} + \vec n\sin \frac{\theta }{2} q=cos2θ+nsin2θ表示惯性坐标系{A}绕向量 n ⃗ \vec n n旋转 θ \theta θ角得到机体坐标系{B}，那么 θ ˙ = A ω ⃗ \dot \theta=^A\vec\omega θ˙=Aω。对两边微分，得 q ˙ = − 1 2 θ ˙ sin θ 2 + 1 2 n ⃗ θ ˙ cos θ 2 + d n ⃗ d t sin θ 2 \dot q = - \frac{1}{2}\dot \theta \sin \frac{\theta }{2} + \frac{1}{2}\vec n\dot \theta \cos \frac{\theta }{2} + \frac{{d\vec n}}{{dt}}\sin \frac{\theta }{2} q˙=−21θ˙sin2θ+21nθ˙cos2θ+dtdnsin2θ
其中 d n ⃗ d t = ϖ × n ⃗ = θ ˙ n ⃗ × n ⃗ = 0 \frac{{d\vec n}}{{dt}} = \varpi \times \vec n = \dot \theta \vec n \times \vec n = 0 dtdn=ϖ×n=θ˙n×n=0所以
q ˙ = − 1 2 θ ˙ sin θ 2 + 1 2 n ⃗ θ ˙ cos θ 2 = n ⃗ θ ˙ 2 ( cos θ 2 + n ⃗ sin θ 2 ) = 1 2 A ω ⃗ q \dot q = - \frac{1}{2}\dot \theta \sin \frac{\theta }{2} + \frac{1}{2}\vec n\dot \theta \cos \frac{\theta }{2} = \vec n\frac{{\dot \theta }}{2}\left( {\cos \frac{\theta }{2} + \vec n\sin \frac{\theta }{2}} \right) = \frac{1}{2} {^A\vec\omega} q q˙=−21θ˙sin2θ+21nθ˙cos2θ=n2θ˙(cos2θ+nsin2θ)=21Aωq B ω ⃗ ^B\vec\omega Bω是机体角速度， B ω ⃗ = q A ω ⃗ q ∗ ^B\vec\omega {\rm{ = }}{q^A}\vec\omega {q^ * } Bω=qAωq∗，所以 q ˙ = 1 2 q B ω ⃗ \dot q = \frac{1}{2} q {^B\vec\omega} q˙=21qBω
q ˙ = ( q 0 + q 1 i ⃗ + q 2 j ⃗ + q 3 k ⃗ ) ( ω x i ⃗ + ω y j ⃗ + ω z k ⃗ ) \dot q =(q_0 + q_1\vec i + q_2\vec j + q_3\vec k)({\omega _x}\vec i + {\omega _y}\vec j + {\omega _z}\vec k) q˙=(q0+q1i+q2j+q3k)(ωxi+ωyj+ωzk) 整理得
四元数微分方程可用来更新四元数，进而更新旋转矩阵。
四旋翼无人机的姿态解算
姿态解算就是求欧拉角 ξ = ( ϕ , θ , ψ ) T \xi {\rm{ = }}{\left( {\phi, \theta ,\psi } \right)^T} ξ=(ϕ,θ,ψ)T，等价于求旋转矩阵。
无人机机体携带的加速度计测加速度向量 B a ⃗ ^B\vec a Ba，陀螺仪测量三个轴的角速度 B ω ⃗ ^B\vec\omega Bω，如果有磁力计可以测地磁场强度向量 B H ⃗ ^B\vec H BH。
先不考虑测量数据的误差，仅凭角速度更新旋转矩阵。使用一阶龙格库塔法更新四元数
q t + Δ t = q t + Δ t q ˙ t {q_{t + \Delta t}} = {q_t} + \Delta t{{\dot q}_t} qt+Δt=qt+Δtq˙t然后四元数单位化，得到四元数表示的旋转矩阵。
传感器的特性
传感器但是有误差的，陀螺仪高频特性好，某一时刻测得的角速度值比较精准，但积分会有很大的漂移；而加速度计和磁力计低频特性好，总体趋势比较准。姿态解算需要利用静态性能好的加速度计和磁力计取补偿动态性能好的陀螺仪，得到不漂并且高速的姿态跟踪算法。
传感器使用前需要校正。陀螺仪校正是测系统初始时一段时间内的测量值的平均值作为偏移值，后面的测量值减去这个偏移值使用；加速度计校正，加速度计测量值分布在一个球面上，用球面方程拟合初始一段时间的数据得到球面半径即为重力加速度的值（单位是g）;地磁场一般情况下大小只有0.5高斯，很容易受到铁钴镍金属和其他磁场的干扰，一般认为干扰磁场是一个恒定的向量。校准方法有平面校准法和立体8字校准法。
加速度补偿陀螺仪
重力加速度 g ⃗ = g z ⃗ \vec g = g\vec z g=gz,归一化 g ^ = z ^ = ( 0 , 0 , 1 ) T \hat g = \hat z=(0,0,1)^T g^=z^=(0,0,1)T，旋转至机体坐标系得 B g ^ ^B\hat g Bg^, B g ^ = A B R z y x A g ^ = ( − sin θ , sin ϕ cos θ , cos ϕ cos θ ) T ^B\hat g = _A^B{R_{zyx}}^A\hat g={\left( { - \sin \theta ,\sin \phi \cos \theta ,\cos \phi \cos \theta } \right)^T} Bg^=ABRzyxAg^=(−sinθ,sinϕcosθ,cosϕcosθ)T（可以看到在载体本身无加速度的情况下加速度计的测量值和角 ψ \psi ψ无关，所以仅凭加速度计无法完全补偿陀螺仪。）
加速度计测得的加速度 B a ⃗ ^B\vec a Ba做归一化 B a ^ ^B\hat a Ba^，向量积得出姿态误差
V e r r o r = B a ^ × B g ^ {V_{error}}{ = ^B}\hat a{ \times ^B}\hat g Verror=Ba^×Bg^向量积误差是指将带有误差的加速度计向量 B a ^ ^B\hat a Ba^转动至与准确的加速度计向量 B g ^ ^B\hat g Bg^重合需要绕什么轴转多少角度。如果完全按照向量积误差转过去，就是完全信任加速度计，如果一点也不转就是完全信任陀螺仪。如果把这个误差乘以一个系数加到角速度上去就是互补滤波。也可以用Mahony的PI滤波, V I + = k i ∗ V e r r o r {V_{I}} += k_i*V_{error} VI+=ki∗Verror G y r o + = k p ∗ V e r r o r + V I Gyro += k_p*V_{error}+{V_{I}} Gyro+=kp∗Verror+VI k p k_p kp是加速度权重，越大则向加速度测量值的收敛越快。 G y r o Gyro Gyro就是得到的修正后的角速度值。
磁力计补偿陀螺仪
加速度计的测量值和角 ψ \psi ψ无关，所以仅凭加速度计无法完全补偿陀螺仪。磁力计直接测得的是地磁场向量 B H ^BH BH，对一个固定地点来说地磁场一般是一定的。这个向量可以分解为两个与当地水平面平行的分量和一个与当地水平面垂直的分量。对于水平方向的两个分量，他们的向量和方向总是指向磁北的。航向角 ψ \psi ψ是就是当前方向和磁北的夹角。
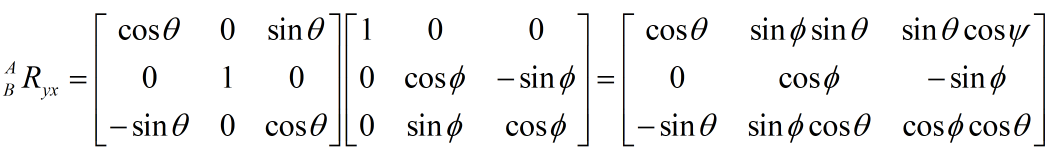A H = B A R y x B H ^AH = _B^A{R_{yx}}^BH AH=BARyxBH如果完全信赖磁力计 ψ = a t a n 2 ( A H y , A H x ) \psi= atan2(^AH_y,^AH_x) ψ=atan2(AHy,AHx)让惯性坐标系的 x x x轴指向磁北，那么 A H = ( A H x , 0 , A H z ) ^AH =(^AH_x,0,^AH_z) AH=(AHx,0,AHz)。 B H = ( B H x , B H y , B H z ) ^BH =(^BH_x,^BH_y,^BH_z) BH=(BHx,BHy,BHz), A H ′ = B A R z y x B H = ( h x , h y , h z ) ^AH' = _B^A{R_{zyx}}^BH=(h_x,h_y,h_z) AH′=BARzyxBH=(hx,hy,hz) A H x = h x 2 + h y 2 , A H z = h z ^A{H_x} = \sqrt {h_x^2 + h_y^2}, ^A{H_z} = {h_z} AHx=hx2+hy2,AHz=hz将 A H ^AH AH旋转至机身坐标系得 B H ′ = A B R z y x A H ^BH '= _A^B{R_{zyx}}^AH BH′=ABRzyxAH， B H ′ ^BH ' BH′和 B H ^BH BH做向量积，向量积误差仍然通过Mahony的PI滤波加到角速度上，这样就完成了一次地磁计的补偿。
四旋翼无人机的控制
PID控制
PID（比例-积分-微分）控制方法是一种简单有效的线性控制方法，广泛应用于工业控制。PID控制是一种单入单出系统的反馈控制方法，输入控制系统目标状态值和实际状态的差值 e e e，得到系统的控制输入 u u u
u = k P e + k I ∫ t 0 t e d t + k D d e d t u = {k_P}e + {k_I}\int_{{t_0}}^t {edt} + {k_D}\frac{{de}}{{dt}} u=kPe+kI∫t0tedt+kDdtde
无人机系统是一个多输入多输出的欠驱动强耦合的非线性系统，控制输入为四个旋翼的升力分别为 F 1 , F 2 , F 3 , F 4 F_1,F_2,F_3,F_4 F1,F2,F3,F4，输出为六个状态 x , y , z , ϕ , θ , ψ {x, y ,z,\phi, \theta ,\psi } x,y,z,ϕ,θ,ψ。不能设计6个独立的PID控制器，因为系统的控制输入只有4个。观察无人机系统的动力学方程 ϕ ¨ = θ ˙ ψ ˙ I y y − I z z I x x + u 2 I x x \ddot \phi = \dot \theta \dot \psi \dfrac{{{I_{yy}} - {I_{zz}}}}{{{I_{xx}}}} + \dfrac{u_2}{{{I_{xx}}}} ϕ¨=θ˙ψ˙IxxIyy−Izz+Ixxu2 θ ¨ = ϕ ˙ ψ ˙ I z z − I x x I y y + u 3 I y y \ddot \theta = \dot \phi \dot \psi \dfrac{{{I_{zz}} - {I_{xx}}}}{{{I_{yy}}}} + \dfrac{u_3}{{{I_{yy}}}} θ¨=ϕ˙ψ˙IyyIzz−Ixx+Iyyu3 ψ ¨ = θ ˙ ϕ ˙ I x x − I y y I z z + u 4 I z z \ddot \psi = \dot \theta \dot \phi \dfrac{{{I_{xx}} - {I_{yy}}}}{{{I_{zz}}}} + \dfrac{u_4}{{{I_{zz}}}} ψ¨=θ˙ϕ˙IzzIxx−Iyy+Izzu4 x ¨ = u 1 ( cos ϕ sin θ cos ψ + sin ϕ sin ψ ) m \ddot x = \dfrac{{u_1(\cos \phi \sin \theta \cos \psi + \sin \phi \sin \psi )}}{m} x¨=mu1(cosϕsinθcosψ+sinϕsinψ) y ¨ = u 1 ( cos ϕ sin θ sin ψ − sin ϕ cos ψ ) m \ddot y = \dfrac{{u_1(\cos \phi \sin \theta \sin \psi - \sin \phi \cos \psi )}}{m} y¨=mu1(cosϕsinθsinψ−sinϕcosψ) z ¨ = u 1 cos ϕ cos θ m − g \ddot z = \dfrac{{u_1\cos \phi \cos \theta }}{m} - g z¨=mu1cosϕcosθ−g1. 因为四旋翼在飞行过程中偏角 ϕ \phi ϕ和 θ \theta θ一般很小，所以近似认为 z z z的状态只与 u 1 u_1 u1有关，所以先用一个独立的PID控制这个通道得到 u 1 u_1 u1。
2. ψ \psi ψ也可近似认为只与 u 4 u_4 u4有关，所以用一个独立的PID控制这个通道得到 u 4 u_4 u4。
3.对 x x x和 y y y通道， x x x和 y y y没有直接和控制量 u 2 u_2 u2和 u 3 u_3 u3产生关系，但是 x x x和 y y y与 ϕ \phi ϕ和 θ \theta θ有关， ϕ \phi ϕ和 θ \theta θ和 u 2 u_2 u2和 u 3 u_3 u3有关，所以对 x x x和 y y y通道分别使用嵌套双层PID控制。如 x x x通道外层PID控制器产生一个虚拟控制律 θ d e s i r e d \theta_{desired} θdesired，作为内层PID控制器的参考输入，内层PID控制器的输入为 θ d e s i r e d − θ \theta_{desired}-\theta θdesired−θ，产生 u 3 u_3 u3， y y y通道类似产生 u 4 u_4 u4。
PID控制是单输入单输出控制，应用于四旋翼无人机控制是把无人机控制分成了四个独立通道，分别控制，忽略了各个通道的耦合关系。
