完全背包:物品可以使用多次
- 完全背包
- 1. 与01背包区别
- 518. 零钱兑换 II
- 1. dp数组以及下标名义
- 2. 递归公式
- 3. dp数组如何初始化
- 4. 遍历顺序:不能颠倒两个for循环顺序
- 5. 代码
- 377. 组合总和 Ⅳ:与零钱兑换类似,但是是求组合数
- 1. dp数组以及下标名义
- 2. 递归公式
- 3. dp数组如何初始化
- 4. 遍历顺序:颠倒两个for循环顺序,先遍历背包再遍历物品
- 5. 代码
完全背包
1. 与01背包区别
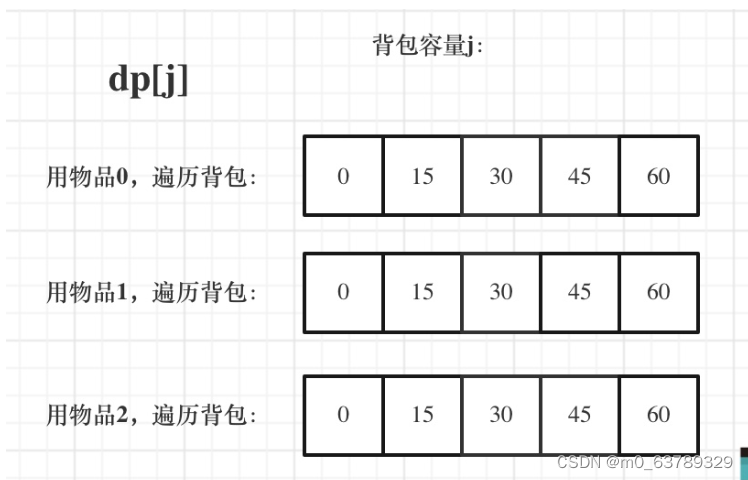
01背包为了物品遍历一次所以用倒序遍历,在完全背包里为了多次使用物品所以用正序遍历
dp[j]:容量为j的背包所能装的最大价值。
01背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}完全背包
// 先遍历物品,再遍历背包
for(int i = 0; i < weight.size(); i++) { // 遍历物品for(int j = weight[i]; j <= bagWeight ; j++) { // 遍历背包容量dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);}
}
518. 零钱兑换 II
1. dp数组以及下标名义
dp[j]:总金额为j的背包所能凑的总数。
2. 递归公式
例如:dp[j],j 为5,
已经有一个1(coins[i]) 的话,有 dp[1]= dp[0]种方法(1种) 凑成 总金额为5的背包。11111
已经有一个2(coins[i]) 的话,有 dp[2] = dp[1] + dp[0]种方法(3种) 凑成 总金额为5的背包。2111/221/11111
已经有一个5 (coins[i])的话,有 dp[5]= dp[2]+ dp[1]+ dp[0].(4种)2111/221/11111/5
递推公式:dp[j] += dp[j - coins[i]];
3. dp数组如何初始化
dp[0] = 1;
4. 遍历顺序:不能颠倒两个for循环顺序
1.外层for循环遍历物品(钱币),内层for遍历背包(金钱总额)的情况:计算组合数
for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量dp[j] += dp[j - coins[i]];}
}
假设:coins[0] = 1,coins[1] = 5。
那么就是先把1加入计算,然后再把5加入计算,得到的方法数量只有{1, 5}这种情况。而不会出现{5, 1}的情况。所以这种遍历顺序中dp[j]里计算的是组合数!
- 交换顺序
for (int j = 0; j <= amount; j++) { // 遍历背包容量for (int i = 0; i < coins.size(); i++) { // 遍历物品if (j - coins[i] >= 0) dp[j] += dp[j - coins[i]];}
}
背包容量的每一个值,都是经过 1 和 5 的计算,包含了{1, 5} 和 {5, 1}两种情况。
此时dp[j]里算出来的就是排列数!
5. 代码
class Solution {
public:int change(int amount, vector<int>& coins) {vector<int>dp(amount + 1, 0);dp[0] = 1;for(int i = 0; i < coins.size(); i++) {//遍历物品for(int j = coins[i]; j <= amount; j++) {//遍历背包dp[j] += dp[j - coins[i]];}}return dp[amount];}
};
377. 组合总和 Ⅳ:与零钱兑换类似,但是是求组合数
1. dp数组以及下标名义
dp[j]:目标整数为j的背包所能凑的组合个数。
2. 递归公式
递推公式:dp[j] += dp[j - coins[i]];
3. dp数组如何初始化
dp[0] = 1;
4. 遍历顺序:颠倒两个for循环顺序,先遍历背包再遍历物品
- 交换顺序
for(int j = 0; j <= target; j++) {//遍历背包for(int i = 0; i < nums.size(); i++) {//遍历物品if(j - nums[i] >= 0 && dp[j] < INT_MAX - dp[j - nums[i]])dp[j] += dp[j - nums[i]];}}
5. 代码
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<int>dp(target + 1, 0);dp[0] = 1;for(int j = 0; j <= target; j++) {//遍历背包for(int i = 0; i < nums.size(); i++) {//遍历物品if(j - nums[i] >= 0 && dp[j] < INT_MAX - dp[j - nums[i]])dp[j] += dp[j - nums[i]];}}return dp[target];}
};
C++测试用例有两个数相加超过int的数据,所以需要在if里加上dp[i] < INT_MAX - dp[i - num]。