文章目录
- 1.多因子模型概述
- 2.因子挖掘
- 3.多因子策略
- 4.多因子策略构建
- 基于多因子的策略通用流程
- Fama-French三因子
- 因子效果测算方法
- 因子测算结论&量化策略构建
东西有点多,拆开成多个文章,边写边整合~,应该会分成2部分:
- 第1部分—因子测算&策略构建
- 策略回测与分析
1.多因子模型概述
多因子模型(Multifactor Model),也是使用最为广泛的模型(神似 y=wx+by=wx+by=wx+b)。
- 因子:资产收益(率)的解释变量
- 多因子模型:是基于“因子”的投资理论构造出的一个模型,用于描述投资的逻辑
因为多因子模型是希望构建“解释变量”来解释最终收益,因此在构造模型的过程中,会存在一些前提条件。想象这样一个场景:过去买了好多股票【股票的组合】,每天都会有当天的损益,最终形成收益曲线图。在整个过程中:
- 因子是用来解释股票本身的,而最终会通过作用于个股价格的涨跌,将损益传递给整个组合
- 因子和当天的损益都是随时间变化的,因此在分析时,因子也是一个时序数据
在多因子模型中,在 ttt 时刻,第 iii 只股票的超额收益率表示为:
ri,t=∑m=1nβi,mXi,m+εi,tr_{i,t} = {\textstyle \sum_{m=1}^{n}} \beta _{i,m} X_{i,m} + \varepsilon _{i,t}ri,t=∑m=1nβi,mXi,m+εi,t
其中 ri,tr_{i,t}ri,t 表示 ttt 时刻第 iii 只股票的超额收益(label值),βi,m\beta _{i,m}βi,m 表示计算出的因子的收益矩阵(模型拟合出的权重矩阵),Xi,mX_{i,m}Xi,m 表示因子的暴露矩阵(指因子的具体取值,也就是x值),εi,t\varepsilon _{i,t}εi,t 表示未被因子解释的特殊收益,即特异性收益率(截距项、误差项)
注:
- 这一部分的内容通常是金融术语,括号里的内容计算机/算法术语;
- 表示多因子模型公式的写法很多,这是其中一种
- 在多因子模型中,最后一项虽然与ML模型中的误差项作用类似,但是在模型中的含义却不同:
- ML中假设每个x独立同分布,因此误差项是服从标准正态分布N(0,1),这个误差项作为先验而存在。
- 多因子模型中由于是为了让解释变量解释收益,所以期望误差项趋近于0,而并非先验的服从什么分布。因为当误差项为0时,代表所有解释变量可以完美解释收益,但目前没有这么牛的模型,所以只能在一定的前提下,让误差项通过检验,来验证模型的可行性。
2.因子挖掘
因子的来源有一个专业术语【因子挖掘】,挖掘出的因子可以被拿来解释个股或组合的收益。目前因子挖掘体系相对成熟,也是入门量化必备的技能。本节中这一部分简单介绍,其他文章中会着重介绍。以CNE7为例,它通过因子的性质将因子分为:
- 风格因子:反映个股状态、预期的因子,体现的是过去一段时期内呈现出的一些特征。比如个股的财务指标,个股市值,PE指标,股价的波动性,换手率等因素
- 行业因子:反映个股所处行业的行业特征。由于行业周期性、政策冲击、重大事件等因素,导致从事相近业务的股票在市场上也会表现出较高的相关性的因素
- 市场因子:更加宏观,反映由于宏观环境影响、供求关系变化呈现出的同涨同跌的情况
挖掘到因子后,判断因子有效性的步骤如下:
- 如果因子的值域范围较大,通常会将数据分箱(或转换为分位数)后,用离散后的值来计算
- 由于因子本身也是时序数据,因此通过滑动窗口的验证会验证很多轮,根据当期的因子值与下期的收益来判断因子的收益
- 每个滑动窗口会得到一个原始因子的 xxx 与最终的收益 yyy,最后通过胜率、均值、方差、相关系数等方法来验证因子的有效性;如使用相关系数验证时,则验证的是 corr(上一期的因子揭露值,本期的收益)corr(上一期的因子揭露值,本期的收益)corr(上一期的因子揭露值,本期的收益)
3.多因子策略
多因子模型适合很多场景,通常来讲,根据模型使用的【因子】的不同,可以将对应的模型分为以下三个类别:
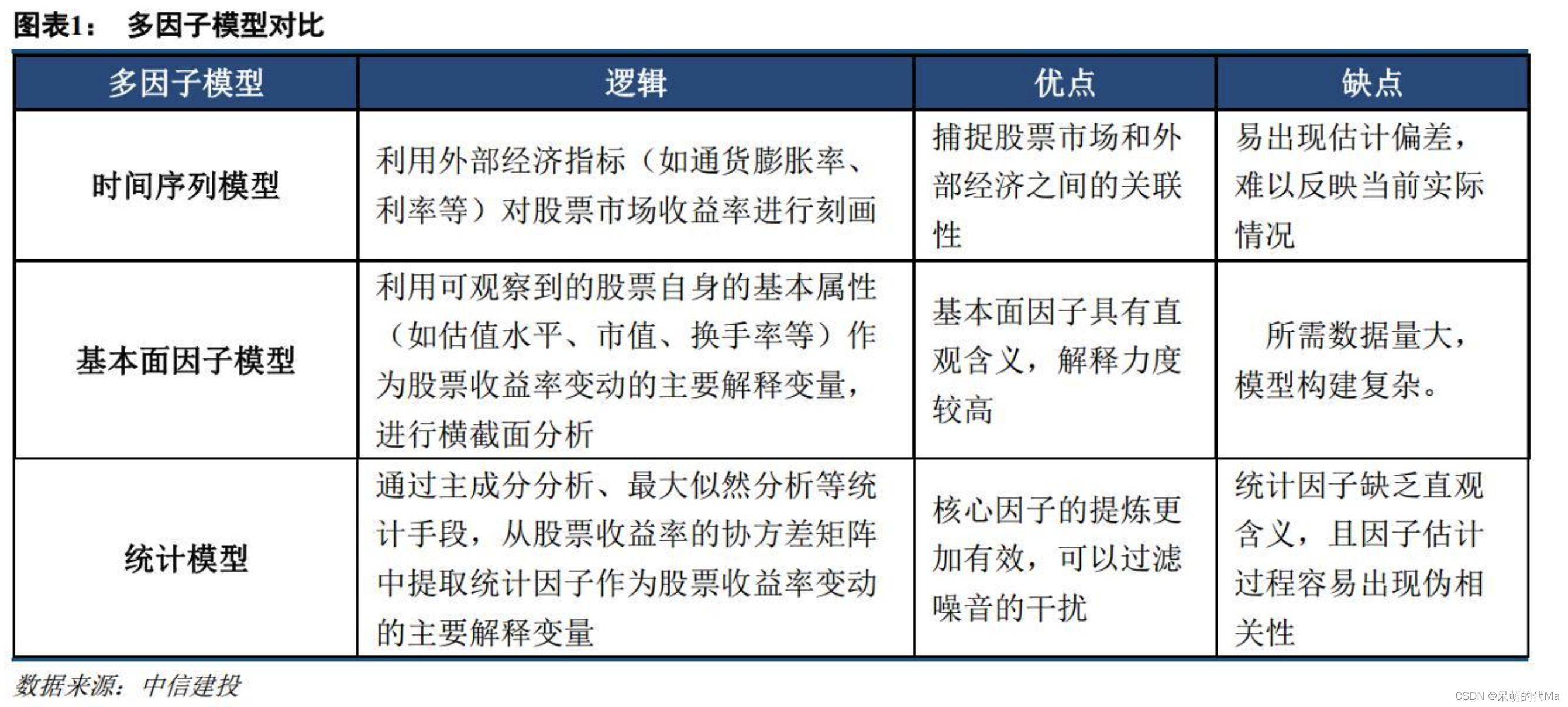
通常来讲,如果我们对金融知识并不了解,特别常见一个操作就是将所有因子排排站,然后按照ML的流程对所有因子进行:特征编码、降维、建模、训练预测。
注:其实这个流程是有一个特别严重的错误操作,我们打过比赛的同学都知道,比如Kaggle里与生物化学相关竞赛、有一定专业性的调查问卷分析等相关竞赛,按照一般的流程是几乎达不到高分,或者说,能够出类拔萃的都不仅仅是建模调参就能达到的。需要对数据做额外的一些操作,比如通过专业领域已有的公式对数据做变化,而变化后的数据可能才是建模的关键。因此,对因子及其背后的金融含义有足够的了解,才能够得到回测时更优的模型。但与此同时伴随着一个风险。我们测算因子的过程就是开天眼的过程,在后续使用中,测算的结论会被先验的代入到后续的计算中。
如果不注意这一点,我们容易把市场当做一个数字游戏或建模任务,而当其他参与者并不这么认为时,风险敞口会在一瞬间出现,造成一定破坏后,在瞬间消失(这里大家可以看一下桥水基金的相关研究,会有更深的感触),同时容易被归因为偶发事件,逻辑不严谨等问题。因为资本是风险最后的承担着,因此在金融领域大家要格外谨慎,谨慎的程度取决于这些钱与你的亲密程度😝。
4.多因子策略构建
基于多因子的策略通用流程
因为多因子模型的“因子”通常是用来解释资产价格变动的解释变量,至于能否盈利需要根据确定的因子来测算,通常构造基于因子的策略流程是:
- 确定因子后,将因子的取值(标准变化、归一化处理)按从小到大(或从大到小)排序
- 根据值域,使用数据分箱处理因子的值,将股票对应的因子归类到十分位之后的类别中
- 做多排名最高的一组中的全部股票(或者等权重做多排名最高的几组股票),有路子的话也同时做空排名最低的一组,每月调整一次仓位
Fama-French三因子
这里我们参考Fama-French三因子模型,百度百科:Fama-French三因子模型
在Fama-French三因子中,在CAPM的市场的基础上,引入了表示价值与规模的解释变量,根据市值与账面市值比(BM,值是市净率的倒数),计算得出HML与SMB:
首先,将股票池的全部股票按照市值的大小分为small小市值与big大市值两类。将大于全市场市值的中位数的股票认为是“大市值股票”,将小于全市场市值的中位数的股票认为是“小市值股票”
其次,统计全市场的账面市值比BM,将前30%认为是Low,将30%-70%认为是Middle,将大于70%的股票认为是High
根据这两个指标,将全市场的股票分为以下两类:
| Low | Middle | High | |
|---|---|---|---|
| Small小市值 | S/L | S/M | S/H |
| Big 大市值 | B/L | B/M | B/H |
- HML(表示价值):12(S/H+B/H)−12(S/L+B/L)\frac{1}{2}(S/H + B/H) - \frac{1}{2} (S/L+B/L)21(S/H+B/H)−21(S/L+B/L)
- SMB(表示规模):13(S/H+S/M+S/L)−13(B/H+B/M+B/L)\frac{1}{3}(S/H + S/M + S/L) - \frac{1}{3} (B/H+B/M+B/L)31(S/H+S/M+S/L)−31(B/H+B/M+B/L)
这里我们简化一下,后续就用市值与BM指标作为因子,来构建量化策略
因子效果测算方法
- 股票池:非ST沪深A股
- 测算时间区间:2015年1月1日至2020年12月23日
测算方法:
- 统计这段时间个股月线的【涨跌幅%】,每个月月末的【市值】,【PB】
- 计算BM指标:BM = 1/PB
- 每月一统计:
- 将大于全市场【市值】的中位数的股票认为是“大市值股票”,将小于全市场市值的中位数的股票认为是“小市值股票”
- 统计全市场的账面市值比BM,将小于30分位数的认为是Low,将30分位-70分位认为是Middle,将大于70分位的股票认为是High
| 市值类别 \ BM类别 | Low | Middle | High |
|---|---|---|---|
| Small小市值 | low_小市值 | middle_小市值 | high_小市值 |
| Big 大市值 | low_大市值 | middle_大市值 | high_大市值 |
- 将下一月的涨跌幅与当月的因子值进行对应,作为因子对未来涨跌幅的解释
最终处理后,得到如下数据表:
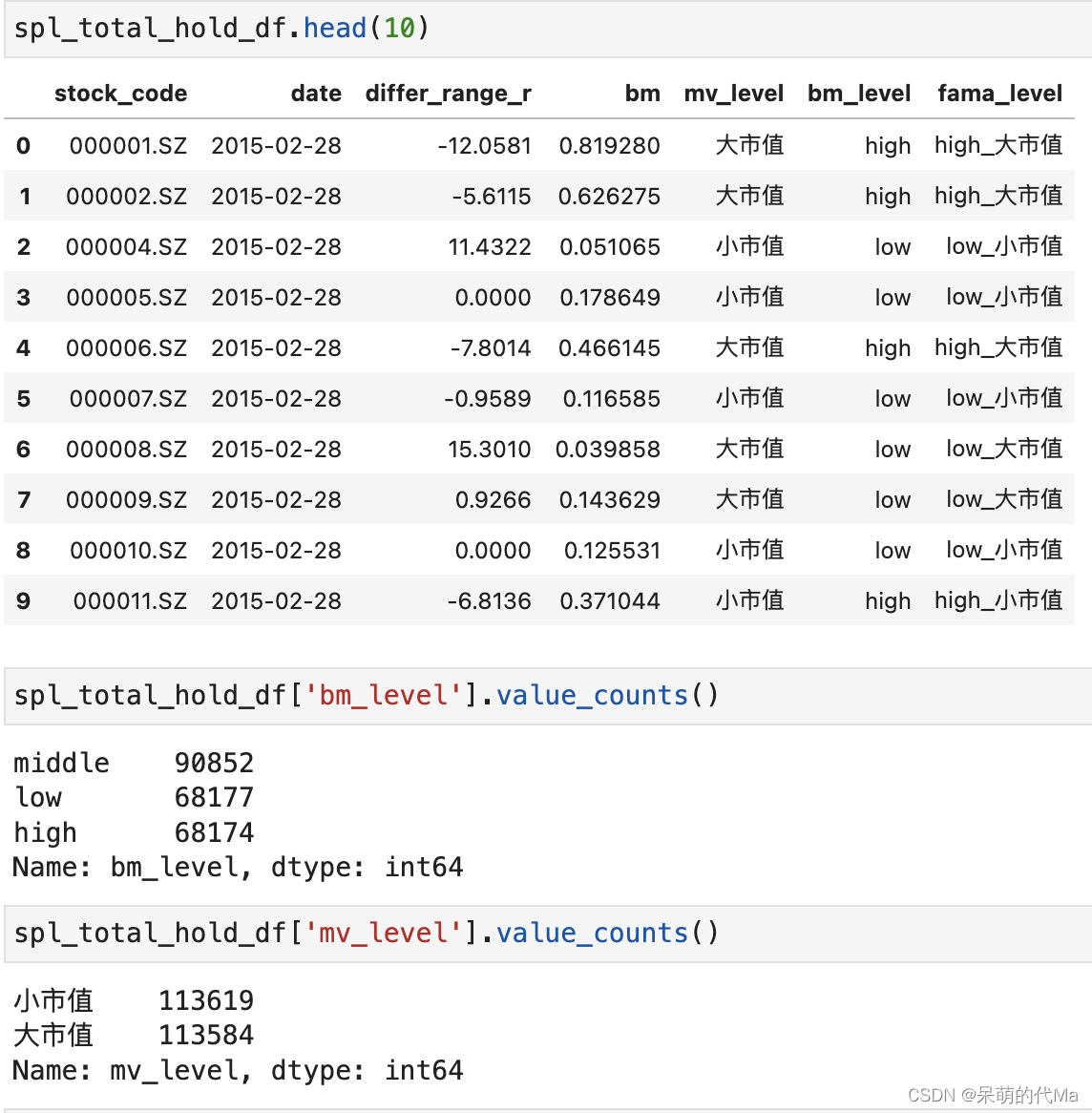
通过对这样的数据进行分析,并得到最终的结果
因子测算结论&量化策略构建
结论如下:
- 综合来看,选择当月BM较低,且市值较大的公司时,胜率最高,高达81.15%;相反的,选择当月BM较高,且市值较小的公司时,胜率最低,低至37.68%
- 逐年测算时,选择当月BM较低,且市值较大的公司时的胜率较为稳定,年均测算结果呈现盈利状态,而其他情况则表现不稳定,时而盈利时而亏损。
注:计算胜率时,收益率大于2%时,记为胜,否则记为负。
月收益如下图所示:
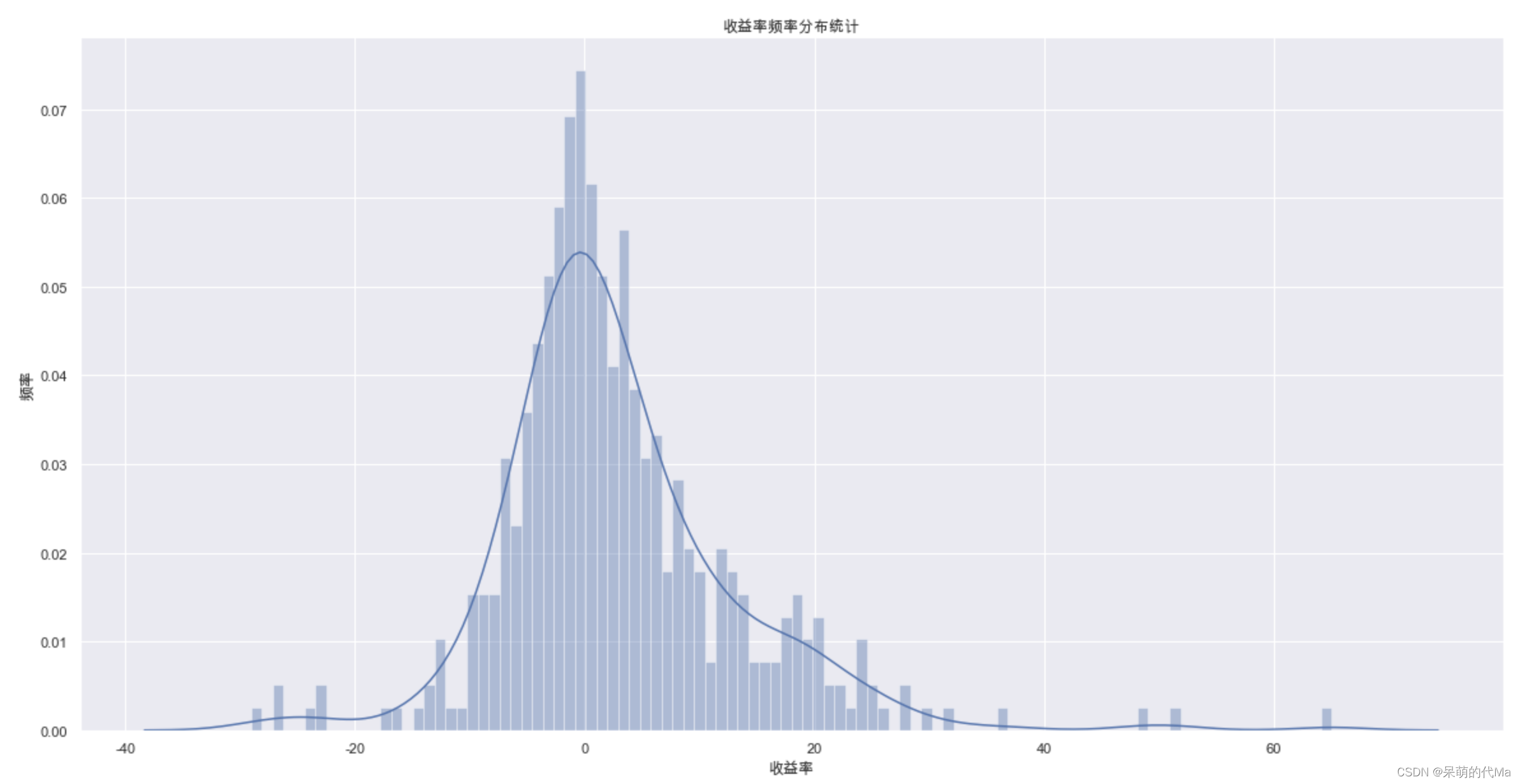
综合来看胜率如下:
| 分类 | 胜率 |
|---|---|
| high_大市值 | 0.449275 |
| high_小市值 | 0.376812 |
| low_大市值 | 0.811594 |
| low_小市值 | 0.666667 |
| middle_大市值 | 0.507246 |
| middle_小市值 | 0.463768 |
按年份统计的胜率图如下所示:

因此,基于Fama-French三因子(灵感来源)的策略就很清晰啦,下一部分我们就买买买,不但看看再过去的表现情况,同时看看在21年与22年的表现效果如何