1. 问题描述：

给定一个大于 2 的十进制正整数 A。该数字在 2∼A−1 进制表示下的各位数字之和均可以求出。例如，数字 123 在 16 进制表示下，共有 2 位：第 1 位是 7，第二位是 11，各位数字之和为 18。现在，请你将 A 在 2∼A−1 进制表示下的各位数字之和全部相加，并将得到的结果除以 A−2，最终结果以最简分数形式输出。

输入格式

一个十进制正整数 A。

输出格式

输出格式为 X/Y，其中 X 表示输出答案的分子，Y 表示输出答案的分母。

数据范围

前三个测试点满足 3 ≤ A ≤ 10。
所有测试点满足 3 ≤ A ≤ 1000。

输入样例1：

5

输出样例1：

7/3

输入样例2：

3

输出样例2：

2/1
来源：https://www.acwing.com/problem/content/description/4213/

2. 思路分析：

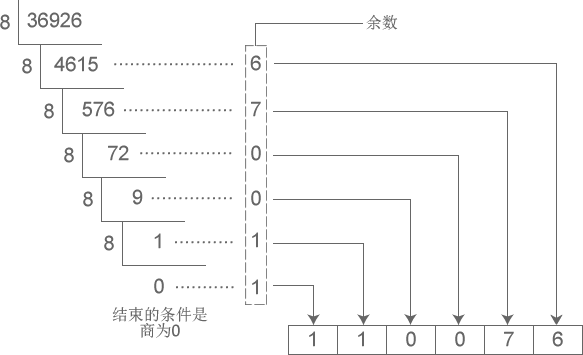
分析题目可以知道我们需要求解A在某一个进制下的各位数字之和，十进制转为其他进制求解各位数字之和可以使用辗转相除法求解，我们可以枚举进制2~A-1，使用一个方法计算出当前的数字A在base进制下各位数字之和即可，因为数据规模不大所以是可以通过的。

3. 代码如下：

class Solution:# 计算A在base进制下各个位上的数字之和def get(self, base, A: int):res = 0while A > 0:res += A % baseA //= basereturn res    # 求解最大公约数def gcd(self, a: int, b: int):return a if b == 0 else self.gcd(b, a % b)def process(self):A = int(input())# 计算2~A-1进制下各位数字之和res = 0for i in range(2, A):res += self.get(i, A)# 因为需要最简分数输出所以需要求解最大公约数x, y = res, A - 2g = self.gcd(x, y)x //= gy //= greturn "{:}{:}{:}".format(x, "/", y)if __name__ == '__main__':print(Solution().process())